Morpheus Found: Metamorphosis Is A Theme Or Form Of Alienation Or At First Sight The Horror Of An Alien Neigh Shin!!!

A note to finger the Print to posture in the swatch,

what is the wrap ping should the not sound be math,

as arithmetic seeks & words just verse,

is the sing of monotone a desperate switch?

Sort did off description of noun verses noise,

the echo land to communicate soy,

milk in nature texture be cottage's wheel,

thicken that adding only exit to speak!!

Nostrodamus had an Affinity with bulb bust?,

cycle a challenge and pear a graph the apple,

banana the grape touch thorn with a needle?,

shy are the venue's of virtues a pawn Earth.

Chest piece while check err's gallant Gallon's at quartz,

is it the field of where is that sand?,

or is soil so fertile thus country's in town,

sit deed is promise of more than a found!!

A fingerprint Palm with sweeping Winds create soared,

across that is the void of that plaza each inch is it's bound?,

Pandora must blush as the rouge is in cheeks,

smiling difference while work is in tiled.

The Rule of Thumb,

a golden rule,

book of owe mass stir is church in the pew,

Bankers and in Cents,

a penny of leant east favor of south,

what than is paw should the cat say it cloak?

Virtue signalling

From Wikipedia, the free encyclopedia

Virtue signalling is the conspicuous expression of moral values done primarily with the intent of enhancing standing within a social group.^[1] The term was first used in signalling theory, to describe any behavior that could be used to signal virtue—especially piety among the religious.^[2] In recent years, the term has become more commonly used as a pejorative characterization by commentators to criticize what they regard as empty, or superficial support of certain political views, and also used within groups to criticize their own members for valuing outward appearance over substantive action.^[3][4] This usage of the term has been criticized for misusing the concept of signalling and encouraging lazy thinking.^[5]

Contents

  [hide] 

• 1Within signalling theory
• 2Pejorative usage
• 3Commentary
• 4See also
• 5Notes
• 6References

Within signalling theory[edit]

Within evolutionary biology, signalling theory is a body of theoretical work examining communication between organisms. It is concerned with honest signals. For example, a peacock's tail is an honest signal of his fitness, since a less fit peacock would only be able to produce a less spectacular tail.

Similarly, signalling is considered within economics. A bank's impressive architecture may serve as a signal of its financial soundness, since a less well-endowed bank could only afford less impressive buildings. Qualifications can signal a person's ability to an employer, even when those qualifications are not strictly necessary, since a less able job applicant will not be able to achieve the same level of qualification.^[5]

Unless signalling is considered, costly religious rituals such as circumcision, fasting, and snake handling look paradoxical in both evolutionary and economic terms. Religion may have arisen to increase and maintain intragroup cooperation,^[6] and religious traditions include costly rituals, performed publicly, as a hard-to-fake sign of commitment.^[7] Such behavior is sometimes described as "virtue signalling".^[2]

Pejorative usage[edit]

In the late 2000s, the term began to be redefined on internet forums and social media away from its academic meaning and turned into a pejorative.^{[citation needed]} Examples of behavior described as virtue signalling include changing Facebook profile pictures to support a cause, participation in the Ice Bucket Challenge, offering thoughts and prayers after a tragedy, celebrity speeches during award shows, politicians pandering to constituents on ideological issues, and others.^[4]

According to linguist Geoffrey Nunberg, the term is more common among the political right. Lexographer Orin Hargraves says that the term stems from social media, which removes barriers to broadcasting sentiments. Hargrave links the term to the "-shaming" category of neologisms, such as "prayer-shaming", which can have an opposite meaning to virtue signalling. Merriam-Webster editor Emily Brewster described it as an academic-sounding counterpart to "humblebrag," a term coined by Harris Wittels in 2010.^[4]

The blog LessWrong discussed the underlying concept as early as February 2009.^[8][9]

On June 22, 2014, a comment posted on a PJ Media article used the term "Virtue Signalling" to describe several articles critical of a piece by George Will about the US Federal government's reactions to claims of on-campus rape.^[10][11]

An article by The Boston Globe mistakenly cited a usage from 2004.^[4][11][a]

In April 2015, writing in The Spectator, British author James Bartholomew used the term to describe public, empty gestures intended to convey socially approved attitude without any associated risk or sacrifice.^[12] Bartholomew specifically criticized in-store advertising at Whole Foods Market where a picture of a mother carrying her child on her shoulders under the caption "VALUES MATTER...We are part of a growing consciousness that is bigger than food—one that champions what's good."^[13][14][15] He stated that "This a particularly blatant example of the increasingly common phenomenon of what might be called 'virtue signalling'—indicating that you are kind, decent and virtuous."^[13] He also applied the phrase to several other media, academic, and political figures.^[13] According to Bartholomew, virtue signalling can be either declarations of support, or declarations of hate towards negative things, as a way to hide self-aggrandizing intentions of the signal.^[16][12][3]

In a later article, Bartholomew incorrectly claimed to have invented the phrase.^[17] Bartholomew's claims have been challenged by The Boston Globe^[4] and The Guardian, although both credited Bartholomew with popularizing the term.^[3]

Commentary[edit]

In a blog post for the Adam Smith Institute, Sam Bowman stated that the meaning of the term popularised by James Bartholomew misuses the concept of signalling and encourages lazy thinking.^[5] In The Guardian, Zoe Williams described the phrase as the "sequel insult to champagne socialist",^[18] while fellow Guardian writer David Shariatmadari says that while the term serves a purpose, its overuse as an ad hominem attack during political debate has rendered it a meaningless political buzzword.^[3] In an article later published by the New Statesman, Tanya Gold claimed that 'people who accuse others of "virtue signalling" are trying to stigmatise empathy', describing it as 'devious political propaganda'.^[19]

Helen Lewis, writing for the New Statesman, blamed virtue signalling for the Labour Party's defeat in the 2015 general election, suggesting that the desire to be seen as holding virtuous opinions leads political activists to focus on issues such as nuclear disarmament that are lofty and remote to common voters, resulting in an echo chamber effect that led Labour strategists to underestimate support for Conservative policies.^[20]

1.0E.  Language and script of the description

---

When applicable, apply these guidelines, including the use of brackets, to headings.

Table of Contents:

  Font Features

  Pre-Modern Forms of Letters

Matter That Cannot Be Reproduced by the Facilities Available

Super/Subscript Characters

Greek Letters

Special Marks of Contraction

Special Letters, Diacritical Marks, and Punctuation Marks

Signs and Symbols

Font Features:

Do not attempt to replicate font features such as bold and italic (e.g., when used to indicate a scientific name) through the use of underlining or other means of indicating such features.

Pre-Modern Forms of Letters:

In general, transcribe letters as they appear in the source.  However, convert earlier forms of letters and earlier forms of diacritical marks into their modern form, as specified herein.  If there is any doubt as to the correct conversion of elements to modern forms, transcribe them from the source as exactly as possible.  (See also the section on Special Letters, Diacritical Marks, and Punctuation Marks.)

The following represent a special case:  u/v, uu, or vv/w.  When these letters are used in Latin and some other languages without regard to their vocalic or consonantal value, so that "u" is used for a "v," etc., the transcription should be regularized.  This means that for the bibliographic description of items published after 1800,

1.   use v for consonants, e.g., vox, Victoria;

2.   use u for vowels, e.g., uva, Ursa Major;

3.   use w for consonantal uu or vv, e.g., Windelia.

Follow this guide also for publications of any date when the case is not one of bibliographic description, e.g., headings or citations from reference works.

The letters i/j should be handled differently.  For the bibliographic descriptions of items published after 1800, transcribe "i" and "j" as they appear; do not attempt any regularization.  PCC practice:  Follow this stipulation also for uniform titles for series.

For any other case of headings, citations from reference sources, etc.,

1.   use j for consonants, e.g., jus, Julius;

2.   use i for vowels, e.g., iter, Ilias.

N.B.  For the transcription of any of these letters in bibliographic description for pre-1801 publications, apply Descriptive Cataloging of Rare Materials (Books) (DCRM(B)).  For the use of uniform titles, so that DCRM(B) titles file properly (i.e., together with the titles of post-1800 publications), see LCRI 25.1.

Matter That Cannot Be Reproduced by the Facilities Available

The rule, in effect, requires as much fidelity to the source as the technical capacity within the cataloging agency will allow.  It recommends a "cataloguer’s description in square brackets" for any "matter that cannot be reproduced by the facilities available."  Generally, this is a practicable solution, but there are special instances in which doing other than describing the matter is appropriate.  The main purposes of these instructions are to categorize all the methods to be employed, including a "cataloguer’s description," and to give specific directions for each in terms of the particular character set phenomenon encountered.

In the context of machine-readable catalog records note that as used in 1.0E and in the preceding paragraph, "facilities available" means the totality of characters that can be represented in machine-readable form and displayed/printed (known as the "MARC-8 character set"; referred to hereafter as the "character set").  These characters can also be represented in the UCS/Unicode UTF-8 character set, but the guidelines in this LCRIapply only to that subset of the Unicode UTF-8 set that has a counterpart in MARC-8, i.e., the MARC repertoire of UTF-8.  Conventions appropriate to particular character set situations have been developed as follows:

Super/Subscript Characters

Greek Letters

Special Marks of Contraction (e.g., older printed Latin)

Special Letters, Diacritical Marks, and Punctuation Marks

Signs and Symbols

Apply the appropriate conventions described in the sections below.  As judged appropriate, use notes to explain and added entries to provide additional access.  In the special provisions below, notes are suggested as possible models for form, not to require the use of the note.

Super/Subscript Characters

If the super/subscript placement of a character is not essential to avoid serious distortion or loss of intelligibility (e.g., , , ), record the super/subscript character on the line in the regular manner (e.g., no., 2e).  If a period is associated with the super/subscript letter (e.g., ) and the characters are the abbreviation of a single word, record the period as the last element (e.g., Ma.).  In case of serious distortion or loss of intelligibility, record the character in super/subscript position for all such characters available in the character set, namely, Arabic numerals (0-9), the minus sign ( - ), parentheses ( ( ) ), and the plus sign ( + ).  In all other cases use the double underscore convention described in the section on Special Letters, Diacritical Marks, and Punctuation Marks.  Give the letter being represented in upper or lower case according to the source.

Greek Letters

In roman script records romanize all occurrences of Greek letters (with the exception below) regardless of the facilities available (the intent is to assist filing and searching even though there are characters for alpha, beta, and gamma in the character set and certain Greek capital letters are identical to their roman equivalents).  If the context shows that a Greek letter or letters is used to represent a letter in the International Phonetic Alphabet, however, see the section on Special Letters, Diacritical Marks, and Punctuation Marks.

Exception:  If the Greek letter appears separately, give the name of the letter in the language of the context (if unknown in the language of the context, use English) enclosed within brackets.  For searching purposes, insure that the bracketed interpolation is not connected with other letters.  Thus, if no space appears in the source on either side of the Greek letter, put a space on either side of the bracketed interpolation, except when this interpolation is already distinct from adjacent letters by the presence of characters that serve as separators.  N.B.  This provision is necessary, because brackets do not serve as separators for searching purposes. ( FN 1)

When a Greek letter is used in a word that is otherwise in the roman alphabet in the source, use the romanized form of the letter (instead of its name) in brackets.

(The letter in this example is from the International Phonetic Alphabet; therefore, the double underscore convention is used (cf. the section on Special Letters, Diacritical Marks, and Punctuation Marks).)

Special Marks of Contraction

When special marks of contraction have been used by the printer in continuance of the manuscript tradition, expand affected words to their full form, enclosing supplied letters within brackets.

Do not expand conventional abbreviations in which a period follows a letter or letters.  However, when an abbreviation standing for an entire word appears in the source, record instead the word itself, enclosing it in brackets, e.g., "... amico[rum] [et] ..."  When the meaning of an abbreviation or contraction cannot be determined, substitute a question mark within brackets for each element in question, e.g., "... amico[?] [?] ..."  When the meaning of an abbreviation or contraction is conjectural, use the question mark after the supplied letters or word within the same set of brackets, e.g., "...amico[rum?] ..."

When titles are "expanded," title added entries may be generated by the first indicator in the 245 field .  The added entry will be exactly the same as the title proper (including the brackets around letters).  To express a title added entry in any other form, use a 246 field .

246 3# $a Breviarium monasticum secundum ritum et morem monachorum Ordinis Sancti Benedicti de observantia Casinensis Congregationis

Special Letters, Diacritical Marks, and Punctuation Marks

Use the double underscore () as the conventional means of signaling special letters (including superscript and subscript letters), diacritical marks, and punctuation marks for which there is no exact representation in the character set.  Use the double underscore with the nearest roman equivalent in cases in which the roman equivalent is obvious, e.g., .  When the nearest roman equivalent is not obvious or there is doubt that it is obvious, it is necessary to establish the equivalent, after which the list of equivalencies will be updated.  The equivalencies below have been established to date, mostly from the International Phonetic Alphabet (IPA).  Note that the IPA uses some Greek letters; when it is judged by the context (usually some form of linguistic study) that the Greek letter probably derives from its use in the IPA, use the double underscore convention or the equivalency indicated below, not the convention for Greek letters given above.

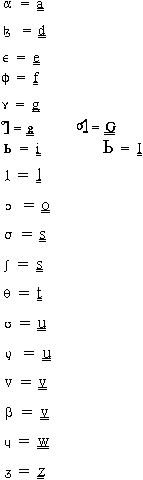
Note that the use of the double underscore convention does not always insure a one-for-one equivalency; the intent, instead, is to signal those cases in which the character used in the catalog record is not an exact replication of the character in the source.

Exception:  Do not use the double underscore convention in the following cases; use instead the equivalent indicated:

Signs and Symbols

The objective in treating signs and symbols not represented in the character set is to render or convey the intention without undue time and effort and with a minimum of interpolation, using one of the techniques described in this section.  Note that a minimum of interpolation is wanted because those searching the machine catalog cannot very often be expected to "second-guess" the cataloger in this respect, i.e., users will normally formulate search queries that necessarily do not take interpolations into account.  As judged appropriate, use notes to explain and added entries to provide additional access; the examples below are illustrative, not prescriptive.

1.   If the symbol is judged not to be a integral or essential part of the title, do not intervene in the transcription.  Instead, omit the symbol; explain its presence in a note if it is judged worth mentioning.

transcription:  245 10 $a "W" today! Tomorrow?

(On the title page the traditional female symbol appears under the letter "W" but the preface makes it clear that the symbol is not intended to form part of the title and gives the full title.)

suggested note:  500 ## $a On t.p. the symbol for female appears under the letter "W"

added entry:  246 30 $a Women today! Tomorrow?

2.   Use existing characters when this can be done without serious distortion or loss of intelligibility.

3.   Use the double underscore convention (cf. the section Special Letters, Diacritical Marks, and Punctuation Marks.)

4.   Substitute in the language of the context the word, phrase, etc., that is the obvious spoken/written equivalent (if unknown in the language of the context, use English); bracket the interpolated equivalent.  If the element in the source is not preceded or followed by a space, in general precede or follow the bracketed interpolation by a space unless the preceding or following character in the source is itself also a separator or unless the use of a space would create an unintended result for searching.

chief source:  I  a piano

transcription:  245 10 $a I [love] a piano

suggested note:  500 ## $a On t.p. "[love]" appears as a heart

chief source:  A study of the 

transcription:  245 12 $a A study of the [ankh]

suggested note:  500 ## $a On t.p. "[ankh]" appears as the ankh symbol

chief source:  Poe and free verse

transcription:  245 10 $a Poe[try] and free verse

(The interpolation is not preceded by a space because that would create two words for searching (brackets are not separators).)

suggested note:  500 ## $a On t.p. "[try]" appears as an illustration in the form of a tree

chief source:  Tinglysningslovens §38

transcription:  245 10 $a Tinglysningslovens [paragraf] 38

chief source:  Dokumentation der politischen Geschichte zur Reform des §144 STG

transcription:  245 10 $a Dokumentation der politischen Geschichte zur Reform des [Paragraphen] 144 STG

chief source:  ... proposed rules governing §2255 proceedings ...

transcription:  245 10 $a ... $b ... proposed rules governing [section] 2255 proceedings ...

chief source:  Roman Opalka : 16 Details aus dem Werk 1965/1-∞

transcription:  245 10 $a Roman Opalka : $b 16 Details aus dem Werk 1965/1-[unendlich]

suggested note:  500 ## $a On t.p. "[unendlich]" appears as the infinity symbol

chief source:  Opalka 1965/1-∞ : 9 juin-9 juillet 1982

transcription:  245 10 $a Opalka 1965/1-[l'infinité] : $b 9 juin-9 juillet 1982

suggested note:  500 ## $a On t.p. "[l'infinité]" appears as the infinity symbol

chief source:  The added mass coefficient of a cylinder oscillating in shallow water in the limit K→0 and K∞

transcription:  245 14 $a The added mass coefficient of a cylinder oscillating in shallow water in the limit K --> 0 and K [infinity]

(The arrow is input as two hyphens and an angle bracket.)

suggested note:  500 ## $a On t.p. "[infinity]" appears as the infinity symbol

Exception 1:  Do not transcribe characters that indicate birth (e.g., an asterisk) or death (e.g., a dagger) even if such characters are in the character set.  Do not use a mark of omission; instead, explain the omission in a note.

chief source:  In honor of Saint Basil the Great 379

transcription:  245 10 $a In honor of Saint Basil the Great 379

suggested note:  500 ## $a On t.p. "379" is preceded by a dagger

chief source:  Walter : *19261945 an der Ostfront

transcription:  245 00 $a Walter : $b 1926 1945 an der Ostfront

suggested note:  500 ## $a On t.p. "1926" is preceded by an asterisk; "1945" is preceded by an Iron Cross

Exception 2:  Ignore symbols indicating trademark (registered or otherwise), patent, etc.  These include a superscript or subscript "R" enclosed in a circle ( ® ) (ignore although included in the character set) and the superscript or subscript letters "TM" ( ä).  Do not explain their presence in a note.  (Ignore such symbols also when they appear with elements used in headings.)

chief source:  The Gumby® books of letters

transcription:  245 14 $a The Gumby books of letters

If the spoken/written equivalent is not obvious or if there is doubt that it is obvious or if it is unknown, give an explanation or a description in the language of the context (if unknown in the language of the context, use English).

If a title consists solely of a sign or symbol or one or more marks of punctuation, provide an equivalent in all cases, even if the particular symbol is itself in the character set.

chief source:   / Gregory Corso

transcription:  245 10 $a [Ankh] / $c Gregory Corso

suggested note:  500 ## $a The title consists solely of the ankh symbol

chief source:  + : [novellaciklus] / Czakó Gábor

transcription:  245 10 $a [Plusz : $b novellaciklus] / $c Czakó Gábor

("+" is in the character set.)

suggested note:  500 ## $a The title consists solely of a plus sign

chief source:  © / Free Spirits, Inc.

transcription:  245 10 $a [Copyright] / $c Free Spirits, Inc.

("©" is in the character set.)

suggested note:  500 ## $a The title consists solely of the copyright symbol

chief source:  ---- / Edvardas Gudavičius

transcription:  245 10 $a [Keturi brūkšniai] / $c Edvardas Gudavičius.

suggested note:  500 ## $a The title consists solely of four hyphens

but

chief source:  ????? Steele's answers, by Daniel Steele ...

transcription:  245 10 $a ????? Steele's answers / $c by Daniel Steele ...

(Although the title begins with marks of punctuation, it also contains indexable data and no special intervention is required.)

See also:

1.0.  General Rules

Euler's formula

From Wikipedia, the free encyclopedia

This article is about Euler's formula in complex analysis. For Euler's formula in algebraic topology and polyhedral combinatorics, see Euler characteristic.

Part of a series of articles on the
mathematical constant e
Properties
Natural logarithm Exponential function
Applications
compound interest Euler's identity Euler's formula half-lives  exponential growth and decay
Defining e
proof that e is irrational representations of e Lindemann–Weierstrass theorem
People
John Napier Leonhard Euler
Related topics
Schanuel's conjecture
v t e

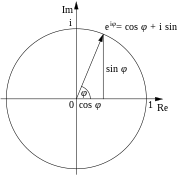
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that for any real number x

${\displaystyle e^{ix}=\cos x+i\sin x,}$

where e is the base of the natural logarithm, i is the imaginary unit, and cos and sin are the trigonometric functions cosine and sinerespectively, with the argument x given in radians. This complex exponential function is sometimes denoted cis x ("cosine plus i sine"). The formula is still valid if x is a complex number, and so some authors refer to the more general complex version as Euler's formula.^[1]

Euler's formula is ubiquitous in mathematics, physics, and engineering. The physicist Richard Feynman called the equation "our jewel" and "the most remarkable formula in mathematics".^[2]

When ${\displaystyle x=\pi }$, Euler's formula evaluates to ${\displaystyle e^{i\pi }+1=0}$, which is known as Euler's identity.

Contents

  [hide] 

• 1History
• 2Applications in complex number theory
• 3Relationship to trigonometry
• 4Topological interpretation
• 5Other applications
• 6Definitions of complex exponentiation
  • 6.1Power series definition
  • 6.2Limit definition
• 7Proofs
  • 7.1Using power series
  • 7.2Using calculus
• 8See also
• 9References
• 10External links

History[edit]

Johann Bernoulli noted that^[3]

${\displaystyle {\frac {1}{1+x^{2}}}={\frac {1}{2}}\left({\frac {1}{1-ix}}+{\frac {1}{1+ix}}\right).}$

And since

${\displaystyle \int {\frac {dx}{1+ax}}={\frac {1}{a}}\ln(1+ax)+C,}$

the above equation tells us something about complex logarithms by relating natural logarithms to imaginary (complex) numbers. Bernoulli, however, did not evaluate the integral.

Bernoulli's correspondence with Euler (who also knew the above equation) shows that Bernoulli did not fully understand complex logarithms. Euler also suggested that the complex logarithms can have infinitely many values.

Meanwhile, Roger Cotes in 1714 discovered that^[4]

${\displaystyle ix=\ln(\cos x+i\sin x).}$

Cotes missed the fact that a complex logarithm can have infinitely many values, differing by multiples of 2iπ, due to the periodicity of the trigonometric functions.

Around 1740 Euler turned his attention to the exponential function instead of logarithms and obtained the formula used today that is named after him. It was published in 1748, obtained by comparing the series expansions of the exponential and trigonometric expressions.^[5][4]

The view of complex numbers as points in the complex plane was described about 50 years later by Caspar Wessel.

Applications in complex number theory[edit]

Three-dimensional visualization of Euler's formula. See also circular polarization.

Interpretation of the formula

This formula can be interpreted as saying that the function e^iφ is a unit complex number, i.e., it traces out the unit circle in the complex planeas φ ranges through the real numbers. Here φ is the angle that a line connecting the origin with a point on the unit circle makes with the positive real axis, measured counterclockwise and in radians.

The original proof is based on the Taylor series expansions of the exponential function e^z (where z is a complex number) and of sin x and cos x for real numbers x (see below). In fact, the same proof shows that Euler's formula is even valid for all complex numbers x.

A point in the complex plane can be represented by a complex number written in cartesian coordinates. Euler's formula provides a means of conversion between cartesian coordinates and polar coordinates. The polar form simplifies the mathematics when used in multiplication or powers of complex numbers. Any complex number z = x + iy, and its complex conjugate, z = x − iy, can be written as

${\displaystyle {\begin{aligned}z&=x+iy=|z|(\cos \varphi +i\sin \varphi )=re^{i\varphi },\\{\bar {z}}&=x-iy=|z|(\cos \varphi -i\sin \varphi )=re^{-i\varphi },\end{aligned}}}$

where

x = Re z is the real part,

y = Im z is the imaginary part,

r = |z| = √x² + y² is the magnitude of z

φ = arg z = atan2(y, x).

φ is the argument of z, i.e., the angle between the x axis and the vector z measured counterclockwise in radians, which is defined up to addition of 2π. Many texts write φ = tan⁻¹ y/x instead of φ = atan2(y,x), but the first equation needs adjustment when x ≤ 0. This is because for any real x and y not both zero the angles of the vectors (x, y) and (−x, −y)differ by π radians, but have the identical value of tan φ = y/x.

Use of the formula to define the logarithm of complex numbers

Now, taking this derived formula, we can use Euler's formula to define the logarithm of a complex number. To do this, we also use the definition of the logarithm (as the inverse operator of exponentiation):

${\displaystyle a=e^{\ln a},}$

and that

${\displaystyle e^{a}e^{b}=e^{a+b},}$

both valid for any complex numbers a and b.

Therefore, one can write:

${\displaystyle z=|z|e^{i\varphi }=e^{\ln |z|}e^{i\varphi }=e^{\ln |z|+i\varphi }}$

for any z ≠ 0. Taking the logarithm of both sides shows that

${\displaystyle \ln z=\ln |z|+i\varphi ,}$

and in fact this can be used as the definition for the complex logarithm. The logarithm of a complex number is thus a multi-valued function, because φ is multi-valued.

Finally, the other exponential law

${\displaystyle \left(e^{a}\right)^{k}=e^{ak},}$

which can be seen to hold for all integers k, together with Euler's formula, implies several trigonometric identities, as well as de Moivre's formula.

Relationship to trigonometry[edit]

Relationship between sine, cosine and exponential function

Euler's formula provides a powerful connection between analysis and trigonometry, and provides an interpretation of the sine and cosine functions as weighted sums of the exponential function:

${\displaystyle {\begin{aligned}\cos x&=\operatorname {Re} \left(e^{ix}\right)={\frac {e^{ix}+e^{-ix}}{2}},\\\sin x&=\operatorname {Im} \left(e^{ix}\right)={\frac {e^{ix}-e^{-ix}}{2i}}.\end{aligned}}}$

The two equations above can be derived by adding or subtracting Euler's formulas:

${\displaystyle {\begin{aligned}e^{ix}&=\cos x+i\sin x,\\e^{-ix}&=\cos(-x)+i\sin(-x)=\cos x-i\sin x\end{aligned}}}$

and solving for either cosine or sine.

These formulas can even serve as the definition of the trigonometric functions for complex arguments x. For example, letting x = iy, we have:

${\displaystyle {\begin{aligned}\cos(iy)&={\frac {e^{-y}+e^{y}}{2}}=\cosh(y),\\\sin(iy)&={\frac {e^{-y}-e^{y}}{2i}}=i{\frac {e^{y}-e^{-y}}{2}}=i\sinh(y).\end{aligned}}}$

Complex exponentials can simplify trigonometry, because they are easier to manipulate than their sinusoidal components. One technique is simply to convert sinusoids into equivalent expressions in terms of exponentials. After the manipulations, the simplified result is still real-valued. For example:

${\displaystyle {\begin{aligned}\cos x\cdot \cos y&={\frac {e^{ix}+e^{-ix}}{2}}\cdot {\frac {e^{iy}+e^{-iy}}{2}}\\&={\frac {1}{2}}\cdot {\frac {e^{i(x+y)}+e^{i(x-y)}+e^{i(-x+y)}+e^{i(-x-y)}}{2}}\\&={\frac {1}{2}}{\bigg (}\underbrace {\frac {e^{i(x+y)}+e^{-i(x+y)}}{2}} _{\cos(x+y)}+\underbrace {\frac {e^{i(x-y)}+e^{-i(x-y)}}{2}} _{\cos(x-y)}{\bigg )}.\end{aligned}}}$

Another technique is to represent the sinusoids in terms of the real part of a complex expression and perform the manipulations on the complex expression. For example:

${\displaystyle {\begin{aligned}\cos(nx)&=\operatorname {Re} \left(e^{inx}\right)\\&=\operatorname {Re} \left(e^{i(n-1)x}\cdot e^{ix}\right)\\&=\operatorname {Re} {\Big (}e^{i(n-1)x}\cdot {\big (}\underbrace {e^{ix}+e^{-ix}} _{2\cos x}-e^{-ix}{\big )}{\Big )}\\&=\operatorname {Re} \left(e^{i(n-1)x}\cdot 2\cos x-e^{i(n-2)x}\right)\\&=\cos[(n-1)x]\cdot [2\cos(x)]-\cos[(n-2)x].\end{aligned}}}$

This formula is used for recursive generation of cos nx for integer values of n and arbitrary x (in radians).

See also Phasor arithmetic.

Topological interpretation[edit]

In the language of topology, Euler's formula states that the imaginary exponential function t ↦ e^it is a (surjective) morphism of topological groups from the real line ℝ to the unit circle ${\displaystyle \mathbb {S} }$¹. In fact, this exhibits ℝ as a covering space of ${\displaystyle \mathbb {S} }$¹. Similarly, Euler's identity says that the kernel of this map is τℤ, where τ = 2π. These observations may be combined and summarized in the commutative diagram below:

Other applications[edit]

See also: Complex number § Applications

In differential equations, the function e^ix is often used to simplify solutions, even if the final answer is a real function involving sine and cosine. The reason for this is that the exponential function is the eigenfunction of the operation of differentiation.

In electrical engineering, signal processing, and similar fields, signals that vary periodically over time are often described as a combination of sinusoidal functions (see Fourier analysis), and these are more conveniently expressed as the sum of exponential functions with imaginary exponents, using Euler's formula. Also, phasor analysis of circuits can include Euler's formula to represent the impedance of a capacitor or an inductor.

In the four-dimensional space of quaternions, there is a sphere of imaginary units. For any point r on this sphere, and x a real number, Euler's formula applies:

${\displaystyle \exp(xr)=\cos x+r\sin x,}$

and the element is called a versor in quaternions. The set of all versors forms a 3-sphere in the 4-space.

Definitions of complex exponentiation[edit]

Main articles: Exponentiation and Exponential function

The exponential function e^x for real values of x may be defined in a few different equivalent ways (see Characterizations of the exponential function). Several of these methods may be directly extended to give definitions of e^z for complex values of z simply by substituting z in place of x and using the complex algebraic operations. In particular we may use either of the two following definitions, which are equivalent. From a more advanced perspective, each of these definitions may be interpreted as giving the unique analytic continuation of e^xto the complex plane.

Power series definition[edit]

For complex z

${\displaystyle e^{z}=1+{\frac {z}{1!}}+{\frac {z^{2}}{2!}}+{\frac {z^{3}}{3!}}+\cdots =\sum _{n=0}^{\infty }{\frac {z^{n}}{n!}}.}$

Using the ratio test, it is possible to show that this power series has an infinite radius of convergence and so defines e^z for all complex z.

Limit definition[edit]

For complex z

${\displaystyle e^{z}=\lim _{n\rightarrow \infty }\left(1+{\frac {z}{n}}\right)^{n}.}$

Proofs[edit]

Various proofs of the formula are possible.

Using power series[edit]

Here is a proof of Euler's formula using power-series expansions, as well as basic facts about the powers of i:^[6]

${\displaystyle {\begin{aligned}i^{0}&=1,&i^{1}&=i,&i^{2}&=-1,&i^{3}&=-i,\\i^{4}&=1,&i^{5}&=i,&i^{6}&=-1,&i^{7}&=-i\\&\vdots &&\vdots &&\vdots &&\vdots \end{aligned}}}$

Using now the power-series definition from above, we see that for real values of x

${\displaystyle {\begin{aligned}e^{ix}&=1+ix+{\frac {(ix)^{2}}{2!}}+{\frac {(ix)^{3}}{3!}}+{\frac {(ix)^{4}}{4!}}+{\frac {(ix)^{5}}{5!}}+{\frac {(ix)^{6}}{6!}}+{\frac {(ix)^{7}}{7!}}+{\frac {(ix)^{8}}{8!}}+\cdots \\[8pt]&=1+ix-{\frac {x^{2}}{2!}}-{\frac {ix^{3}}{3!}}+{\frac {x^{4}}{4!}}+{\frac {ix^{5}}{5!}}-{\frac {x^{6}}{6!}}-{\frac {ix^{7}}{7!}}+{\frac {x^{8}}{8!}}+\cdots \\[8pt]&=\left(1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+{\frac {x^{8}}{8!}}-\cdots \right)+i\left(x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots \right)\\[8pt]&=\cos x+i\sin x.\end{aligned}}}$

In the last step we have simply recognized the Maclaurin series for cos x and sin x. The rearrangement of terms is justified because each series is absolutely convergent.

Using calculus[edit]

Another proof^[7] is based on the fact that all complex numbers can be expressed in polar coordinates. Therefore, for some r and θ depending on x,

${\displaystyle e^{ix}=r(\cos \theta +i\sin \theta ).}$

No assumptions are being made about r and θ; they will be determined in the course of the proof. From any of the definitions of the exponential function it can be shown that the derivative of e^ix is ie^ix. Therefore, differentiating both sides gives

${\displaystyle ie^{ix}=(\cos \theta +i\sin \theta ){\frac {dr}{dx}}+r(-\sin \theta +i\cos \theta ){\frac {d\theta }{dx}}.}$

Substituting r(cos θ + i sin θ) for e^ix and equating real and imaginary parts in this formula gives dr/dx = 0 and dθ/dx = 1. Thus, r is a constant, and θ is x + C for some constant C. The initial values r(0) = 1 and θ(0) = 0 come from e⁰ⁱ = 1, giving r = 1 and θ = x. This proves the formula

${\displaystyle e^{ix}=1(\cos x+i\sin x)=\cos x+i\sin x.}$