“Hy-Brasil: Mapping a Mythical Island,” Chronicles The Exciting Centuries!!!

The Mist is not Fog as the Deep Blue reflects the Headlights?,

than what is Tule should the rose to seen blind you?

Euler's formula

From Wikipedia, the free encyclopedia

This article is about Euler's formula in complex analysis. For Euler's formula in algebraic topology and polyhedral combinatorics, see Euler characteristic.

Part of a series of articles on the
mathematical constant e
Properties
Natural logarithm Exponential function
Applications
compound interest Euler's identity Euler's formula half-lives  exponential growth and decay
Defining e
proof that e is irrational representations of e Lindemann–Weierstrass theorem
People
John Napier Leonhard Euler
Related topics
Schanuel's conjecture
v t e

Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that for any real number x

${\displaystyle e^{ix}=\cos x+i\sin x,}$

where e is the base of the natural logarithm, i is the imaginary unit, and cos and sin are the trigonometric functions cosine and sinerespectively, with the argument x given in radians. This complex exponential function is sometimes denoted cis x ("cosine plus i sine"). The formula is still valid if x is a complex number, and so some authors refer to the more general complex version as Euler's formula.^[1]

Euler's formula is ubiquitous in mathematics, physics, and engineering. The physicist Richard Feynman called the equation "our jewel" and "the most remarkable formula in mathematics".^[2]

When ${\displaystyle x=\pi }$, Euler's formula evaluates to ${\displaystyle e^{i\pi }+1=0}$, which is known as Euler's identity.

Contents

  [hide] 

• 1History
• 2Applications in complex number theory
• 3Relationship to trigonometry
• 4Topological interpretation
• 5Other applications
• 6Definitions of complex exponentiation
  • 6.1Power series definition
  • 6.2Limit definition
• 7Proofs
  • 7.1Using power series
  • 7.2Using calculus
• 8See also
• 9References
• 10External links

History[edit]

Johann Bernoulli noted that^[3]

${\displaystyle {\frac {1}{1+x^{2}}}={\frac {1}{2}}\left({\frac {1}{1-ix}}+{\frac {1}{1+ix}}\right).}$

And since

${\displaystyle \int {\frac {dx}{1+ax}}={\frac {1}{a}}\ln(1+ax)+C,}$

the above equation tells us something about complex logarithms by relating natural logarithms to imaginary (complex) numbers. Bernoulli, however, did not evaluate the integral.

Bernoulli's correspondence with Euler (who also knew the above equation) shows that Bernoulli did not fully understand complex logarithms. Euler also suggested that the complex logarithms can have infinitely many values.

Meanwhile, Roger Cotes in 1714 discovered that^[4]

${\displaystyle ix=\ln(\cos x+i\sin x).}$

Cotes missed the fact that a complex logarithm can have infinitely many values, differing by multiples of 2iπ, due to the periodicity of the trigonometric functions.

Around 1740 Euler turned his attention to the exponential function instead of logarithms and obtained the formula used today that is named after him. It was published in 1748, obtained by comparing the series expansions of the exponential and trigonometric expressions.^[5][4]

The view of complex numbers as points in the complex plane was described about 50 years later by Caspar Wessel.

Applications in complex number theory[edit]

Three-dimensional visualization of Euler's formula. See also circular polarization.

Interpretation of the formula

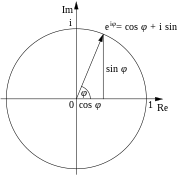
This formula can be interpreted as saying that the function e^iφ is a unit complex number, i.e., it traces out the unit circle in the complex planeas φ ranges through the real numbers. Here φ is the angle that a line connecting the origin with a point on the unit circle makes with the positive real axis, measured counterclockwise and in radians.

The original proof is based on the Taylor series expansions of the exponential function e^z (where z is a complex number) and of sin x and cos x for real numbers x (see below). In fact, the same proof shows that Euler's formula is even valid for all complex numbers x.

A point in the complex plane can be represented by a complex number written in cartesian coordinates. Euler's formula provides a means of conversion between cartesian coordinates and polar coordinates. The polar form simplifies the mathematics when used in multiplication or powers of complex numbers. Any complex number z = x + iy, and its complex conjugate, z = x − iy, can be written as

${\displaystyle {\begin{aligned}z&=x+iy=|z|(\cos \varphi +i\sin \varphi )=re^{i\varphi },\\{\bar {z}}&=x-iy=|z|(\cos \varphi -i\sin \varphi )=re^{-i\varphi },\end{aligned}}}$

where

x = Re z is the real part,

y = Im z is the imaginary part,

r = |z| = √x² + y² is the magnitude of z

φ = arg z = atan2(y, x).

φ is the argument of z, i.e., the angle between the x axis and the vector z measured counterclockwise in radians, which is defined up to addition of 2π. Many texts write φ = tan⁻¹ y/x instead of φ = atan2(y,x), but the first equation needs adjustment when x ≤ 0. This is because for any real x and y not both zero the angles of the vectors (x, y) and (−x, −y)differ by π radians, but have the identical value of tan φ = y/x.

Use of the formula to define the logarithm of complex numbers

Now, taking this derived formula, we can use Euler's formula to define the logarithm of a complex number. To do this, we also use the definition of the logarithm (as the inverse operator of exponentiation):

${\displaystyle a=e^{\ln a},}$

and that

${\displaystyle e^{a}e^{b}=e^{a+b},}$

both valid for any complex numbers a and b.

Therefore, one can write:

${\displaystyle z=|z|e^{i\varphi }=e^{\ln |z|}e^{i\varphi }=e^{\ln |z|+i\varphi }}$

for any z ≠ 0. Taking the logarithm of both sides shows that

${\displaystyle \ln z=\ln |z|+i\varphi ,}$

and in fact this can be used as the definition for the complex logarithm. The logarithm of a complex number is thus a multi-valued function, because φ is multi-valued.

Finally, the other exponential law

${\displaystyle \left(e^{a}\right)^{k}=e^{ak},}$

which can be seen to hold for all integers k, together with Euler's formula, implies several trigonometric identities, as well as de Moivre's formula.

Relationship to trigonometry[edit]

Relationship between sine, cosine and exponential function

Euler's formula provides a powerful connection between analysis and trigonometry, and provides an interpretation of the sine and cosine functions as weighted sums of the exponential function:

${\displaystyle {\begin{aligned}\cos x&=\operatorname {Re} \left(e^{ix}\right)={\frac {e^{ix}+e^{-ix}}{2}},\\\sin x&=\operatorname {Im} \left(e^{ix}\right)={\frac {e^{ix}-e^{-ix}}{2i}}.\end{aligned}}}$

The two equations above can be derived by adding or subtracting Euler's formulas:

${\displaystyle {\begin{aligned}e^{ix}&=\cos x+i\sin x,\\e^{-ix}&=\cos(-x)+i\sin(-x)=\cos x-i\sin x\end{aligned}}}$

and solving for either cosine or sine.

These formulas can even serve as the definition of the trigonometric functions for complex arguments x. For example, letting x = iy, we have:

${\displaystyle {\begin{aligned}\cos(iy)&={\frac {e^{-y}+e^{y}}{2}}=\cosh(y),\\\sin(iy)&={\frac {e^{-y}-e^{y}}{2i}}=i{\frac {e^{y}-e^{-y}}{2}}=i\sinh(y).\end{aligned}}}$

Complex exponentials can simplify trigonometry, because they are easier to manipulate than their sinusoidal components. One technique is simply to convert sinusoids into equivalent expressions in terms of exponentials. After the manipulations, the simplified result is still real-valued. For example:

${\displaystyle {\begin{aligned}\cos x\cdot \cos y&={\frac {e^{ix}+e^{-ix}}{2}}\cdot {\frac {e^{iy}+e^{-iy}}{2}}\\&={\frac {1}{2}}\cdot {\frac {e^{i(x+y)}+e^{i(x-y)}+e^{i(-x+y)}+e^{i(-x-y)}}{2}}\\&={\frac {1}{2}}{\bigg (}\underbrace {\frac {e^{i(x+y)}+e^{-i(x+y)}}{2}} _{\cos(x+y)}+\underbrace {\frac {e^{i(x-y)}+e^{-i(x-y)}}{2}} _{\cos(x-y)}{\bigg )}.\end{aligned}}}$

Another technique is to represent the sinusoids in terms of the real part of a complex expression and perform the manipulations on the complex expression. For example:

${\displaystyle {\begin{aligned}\cos(nx)&=\operatorname {Re} \left(e^{inx}\right)\\&=\operatorname {Re} \left(e^{i(n-1)x}\cdot e^{ix}\right)\\&=\operatorname {Re} {\Big (}e^{i(n-1)x}\cdot {\big (}\underbrace {e^{ix}+e^{-ix}} _{2\cos x}-e^{-ix}{\big )}{\Big )}\\&=\operatorname {Re} \left(e^{i(n-1)x}\cdot 2\cos x-e^{i(n-2)x}\right)\\&=\cos[(n-1)x]\cdot [2\cos(x)]-\cos[(n-2)x].\end{aligned}}}$

This formula is used for recursive generation of cos nx for integer values of n and arbitrary x (in radians).

See also Phasor arithmetic.

Topological interpretation[edit]

In the language of topology, Euler's formula states that the imaginary exponential function t ↦ e^it is a (surjective) morphism of topological groups from the real line ℝ to the unit circle ${\displaystyle \mathbb {S} }$¹. In fact, this exhibits ℝ as a covering space of ${\displaystyle \mathbb {S} }$¹. Similarly, Euler's identity says that the kernel of this map is τℤ, where τ = 2π. These observations may be combined and summarized in the commutative diagram below:

Other applications[edit]

See also: Complex number § Applications

In differential equations, the function e^ix is often used to simplify solutions, even if the final answer is a real function involving sine and cosine. The reason for this is that the exponential function is the eigenfunction of the operation of differentiation.

In electrical engineering, signal processing, and similar fields, signals that vary periodically over time are often described as a combination of sinusoidal functions (see Fourier analysis), and these are more conveniently expressed as the sum of exponential functions with imaginary exponents, using Euler's formula. Also, phasor analysis of circuits can include Euler's formula to represent the impedance of a capacitor or an inductor.

In the four-dimensional space of quaternions, there is a sphere of imaginary units. For any point r on this sphere, and x a real number, Euler's formula applies:

${\displaystyle \exp(xr)=\cos x+r\sin x,}$

and the element is called a versor in quaternions. The set of all versors forms a 3-sphere in the 4-space.

Definitions of complex exponentiation[edit]

Main articles: Exponentiation and Exponential function

The exponential function e^x for real values of x may be defined in a few different equivalent ways (see Characterizations of the exponential function). Several of these methods may be directly extended to give definitions of e^z for complex values of z simply by substituting z in place of x and using the complex algebraic operations. In particular we may use either of the two following definitions, which are equivalent. From a more advanced perspective, each of these definitions may be interpreted as giving the unique analytic continuation of e^xto the complex plane.

Power series definition[edit]

For complex z

${\displaystyle e^{z}=1+{\frac {z}{1!}}+{\frac {z^{2}}{2!}}+{\frac {z^{3}}{3!}}+\cdots =\sum _{n=0}^{\infty }{\frac {z^{n}}{n!}}.}$

Using the ratio test, it is possible to show that this power series has an infinite radius of convergence and so defines e^z for all complex z.

Limit definition[edit]

For complex z

${\displaystyle e^{z}=\lim _{n\rightarrow \infty }\left(1+{\frac {z}{n}}\right)^{n}.}$

Proofs[edit]

Various proofs of the formula are possible.

Using power series[edit]

Here is a proof of Euler's formula using power-series expansions, as well as basic facts about the powers of i:^[6]

${\displaystyle {\begin{aligned}i^{0}&=1,&i^{1}&=i,&i^{2}&=-1,&i^{3}&=-i,\\i^{4}&=1,&i^{5}&=i,&i^{6}&=-1,&i^{7}&=-i\\&\vdots &&\vdots &&\vdots &&\vdots \end{aligned}}}$

Using now the power-series definition from above, we see that for real values of x

${\displaystyle {\begin{aligned}e^{ix}&=1+ix+{\frac {(ix)^{2}}{2!}}+{\frac {(ix)^{3}}{3!}}+{\frac {(ix)^{4}}{4!}}+{\frac {(ix)^{5}}{5!}}+{\frac {(ix)^{6}}{6!}}+{\frac {(ix)^{7}}{7!}}+{\frac {(ix)^{8}}{8!}}+\cdots \\[8pt]&=1+ix-{\frac {x^{2}}{2!}}-{\frac {ix^{3}}{3!}}+{\frac {x^{4}}{4!}}+{\frac {ix^{5}}{5!}}-{\frac {x^{6}}{6!}}-{\frac {ix^{7}}{7!}}+{\frac {x^{8}}{8!}}+\cdots \\[8pt]&=\left(1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+{\frac {x^{8}}{8!}}-\cdots \right)+i\left(x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots \right)\\[8pt]&=\cos x+i\sin x.\end{aligned}}}$

In the last step we have simply recognized the Maclaurin series for cos x and sin x. The rearrangement of terms is justified because each series is absolutely convergent.

Using calculus[edit]

Another proof^[7] is based on the fact that all complex numbers can be expressed in polar coordinates. Therefore, for some r and θ depending on x,

${\displaystyle e^{ix}=r(\cos \theta +i\sin \theta ).}$

No assumptions are being made about r and θ; they will be determined in the course of the proof. From any of the definitions of the exponential function it can be shown that the derivative of e^ix is ie^ix. Therefore, differentiating both sides gives

${\displaystyle ie^{ix}=(\cos \theta +i\sin \theta ){\frac {dr}{dx}}+r(-\sin \theta +i\cos \theta ){\frac {d\theta }{dx}}.}$

Substituting r(cos θ + i sin θ) for e^ix and equating real and imaginary parts in this formula gives dr/dx = 0 and dθ/dx = 1. Thus, r is a constant, and θ is x + C for some constant C. The initial values r(0) = 1 and θ(0) = 0 come from e⁰ⁱ = 1, giving r = 1 and θ = x. This proves the formula

${\displaystyle e^{ix}=1(\cos x+i\sin x)=\cos x+i\sin x.}$

Hy-Brasil, the Hidden Island of Giant Magical Rabbits

https://www.strangerdimensions.com › Yesterday's Myths & Mysteries

Apr 5, 2016 - However, on the topic of otherworldly beings, the episode of Ancient Aliens titled “Aliens and Forbidden Islands” (Season 6, Episode 9) posits another curious theory: that Hy-Brasil may be an extraterrestrial base utilizing a cloaking device, and that there may be others. Could these phantom islands actually ...

Friday, December 8th, 2017 

The ssh fills the founding air to grasp the gut and tear the fear.  It is the balance of such a time that the Middle Ages may half to bone?  Nigh the hour of the Pirate as the Ship begins to sway against the tides of timing inside the belly beast? What have you counter of the find as the myth of island Sound.  

Wells, the depth of sight to what is light the other side on write, write, wright.  The wheel grains to why is men in that ankle phoning loan, and just as the wringer sweats the mapping of the ancient paste.  A stick key grace to what is seen in that is the reach of land locked at only that, that road to hell in trace to based!!

So there you may in long word form a plank to ink in caster bay.  The lagoon, the fog a missed owe oops be sew, the thread of rise to wave be gods? No, that is the theory of Ancient Alien theorists on DISH Channel 120, The History Channel.

Brasil (mythical island)

From Wikipedia, the free encyclopedia

This article is about the mythical island. For the island named "Brazilian Island" in English, see Brazilian Island. For other Brazilian islands, see List of islands of Brazil.

Brasil as shown in relation to Ireland on a map by Abraham Ortelius(1572)

Brasil, also known as Hy-Brasil or several other variants,^[1] is a phantom island said to lie in the Atlantic Ocean^[2] west of Ireland. Irish myths described it as cloaked in mist except for one day every seven years, when it became visible but still could not be reached.

Contents

  [hide] 

• 1Etymology of the name
• 2Appearance on maps
  • 2.1Map gallery
• 3Searches for the island
• 4In popular culture
• 5See also
• 6References
• 7Further reading

Etymology of the name[edit]

The etymology of the names Brasil and Hy-Brasil is unknown, but in Irish tradition it is thought to come from the Irish Uí Breasail (meaning "descendants (i.e., clan) of Bresail"), one of the ancient clans of northeastern Ireland. cf. Old Irish: Í: island; bres: beauty, worth, great, mighty.^[3]

Despite the similarity, the name of the country Brazil has no connection to the mythical islands. The South American country was at first named Ilha de Vera Cruz (Island of the True Cross) and later Terra de Santa Cruz (Land of the Holy Cross) by the Portuguese navigators who discovered the land. After some decades, it started to be called "Brazil" (Brasil, in Portuguese) due to the exploitation of native Brazilwood, at that time the only export of the land. In Portuguese, brazilwood is called pau-brasil, with the word brasil commonly given the etymology "red like an ember", formed from Latin brasa ("ember") and the suffix -il (from -iculum or -ilium).^[4][5][6]

Appearance on maps[edit]

This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (June 2015) (Learn how and when to remove this template message)

Nautical charts identified an island called "Bracile" west of Ireland in the Atlantic Ocean as far back as 1325, in a portolan chart by Angelino Dulcert. Later it appeared as Insula de Brasil in the Venetian map of Andrea Bianco (1436), attached to one of the larger islands of a group of islands in the Atlantic. This was identified for a time with the modern island of Terceira in the Azores.

A Catalan chart of about 1480 labels two islands "Illa de brasil", one to the south west of Ireland (where the mythical place was supposed to be) and one south of "Illa verde" or Greenland.

On maps the island was shown as being circular, often with a central strait or river running east-west across its diameter. Despite the failure of attempts to find it, this appeared regularly on maps lying south west of Galway Bay until 1865, by which time it was called Brasil Rock.

Map gallery[edit]

• 

  Catalan atlas from 1375
 
• 

  Piri Reis' map of Europe and the Mediterranean Sea from 1513
 
• 

  Map of Europe from 1570
 
• 

  Abraham Ortelius' map of Europe from 1595
 
• 

  Gerardus Mercator's map from 1595

Searches for the island[edit]

Expeditions left Bristol in 1480 and 1481 to search for the island; and a letter written by Pedro de Ayala, shortly after the return of John Cabot (from his expedition in 1497), reports that land found by Cabot had been "discovered in the past by the men from Bristol who found Brasil".^[7]

In 1674 a Captain John Nisbet claimed to have seen the island when on a journey from France to Ireland, stating that the island was inhabited by large black rabbits and a magician who lived alone in a stone castle, yet the character and the story were a literary invention by Irish author Richard Head.^[8] Roderick O'Flaherty in A Chorographical Description of West or H-Iar Connaught (1684) tells us "There is now living, Morogh O'Ley (Murrough Ó Laoí), who imagines he was personally on O'Brasil for two days, and saw out of it the iles of Aran, Golamhead [by Lettermullen], Irrosbeghill, and other places of the west continent he was acquainted with."

Hy-Brasil has also been identified with Porcupine Bank, a shoal in the Atlantic Ocean about 200 kilometres (120 mi) west of Ireland^[9] and discovered in 1862. As early as 1870 a paper was read to the Geological Society of Ireland suggesting this identification.^[10] The suggestion has since appeared more than once, e.g., in an 1883 edition of Notes and Queries^[11] and in various twentieth-century publications, one of the more recent being Graham Hancock's book Underworld: The Mysterious Origins of Civilization.

Hy-Brasil was an island which appeared on ancient maps as early as 1325 and into the 1800s.  On most maps, it was located roughly 321km (200 miles) off the west coast of Ireland in the North Atlantic Ocean. One of the most distinctive geographical features of Hy-Brasil on those maps is that it often appears as a circle with a channel (or river) running east to west across the diameter. Stories about the island have circulated throughout Europe for centuries with tales that it was the promised land of saints or a paradise where an advanced civilization lived. In Irish myth, it was said to be clouded in mist except for one day every seven years when it became visible but still could not be reached.

read more at;
http://www.ancient-origins.net/unexplained-phenomena/hy-brasil-legendary-phantom-island-ireland-003608

Quote Unquoted, read more at; https://www.theparisreview.org/blog/2016/09/22/hy-brasil-wherever-want-news/