Philosophiæ Naturalis Principia Mathematica

Philosophiæ Naturalis Principia Mathematica
	Title page of Principia, first edition (1687)
Author	Isaac Newton
Original title	Philosophiæ Naturalis Principia Mathematica
Country	England
Language	Neo-Latin
Publication date	1687
Published in English	1728
LC Class	QA803 .A53
Original text	Philosophiæ Naturalis Principia Mathematica at Latin Wikisource
Translation	Philosophiæ Naturalis Principia Mathematica at Wikisource

Philosophiæ Naturalis Principia Mathematica (English: The Mathematical Principles of Natural Philosophy)^[1] often referred to as simply the Principia (/prɪnˈsɪpiə, prɪnˈkɪpiə/), is a book by Isaac Newtonthat expounds Newton's laws of motion and his law of universal gravitation. The Principia is written in Latinand comprises three volumes, and was first published on 5 July 1687.^[2]^[3]

The Principia is considered one of the most important works in the history of science.^[4] The French mathematical physicist Alexis Clairaut assessed it in 1747: "The famous book of Mathematical Principles of Natural Philosophy marked the epoch of a great revolution in physics. The method followed by its illustrious author Sir Newton ... spread the light of mathematics on a science which up to then had remained in the darkness of conjectures and hypotheses."^[5] Joseph-Louis Lagrange described it as "the greatest production of a human mind".^[6]

A more recent assessment has been that while acceptance of Newton's laws was not immediate, by the end of the century after publication in 1687, "no one could deny that [out of the Principia] a science had emerged that, at least in certain respects, so far exceeded anything that had ever gone before that it stood alone as the ultimate exemplar of science generally".^[7]

The Principia forms a mathematical foundation for the theory of classical mechanics. Among other achievements, it explains Johannes Kepler's laws of planetary motion, which Kepler had first obtained empirically. In formulating his physical laws, Newton developed and used mathematical methods now included in the field of calculus, expressing them in the form of geometric propositions about "vanishingly small" shapes.^[8] In a revised conclusion to the Principia (see § General Scholium), Newton emphasized the empirical nature of the work with the expression Hypotheses non fingo ("I frame/feign no hypotheses").^[9]

After annotating and correcting his personal copy of the first edition,^[10] Newton published two further editions, during 1713^[11] with errors of the 1687 corrected, and an improved version^[12] of 1726.^[11]

Contents[edit]

Expressed aim and topics covered[edit]

The Preface of the work states:^[13]

... Rational Mechanics will be the sciences of motion resulting from any forces whatsoever, and of the forces required to produce any motion, accurately proposed and demonstrated ... And therefore we offer this work as mathematical principles of his philosophy. For all the difficulty of philosophy seems to consist in this—from the phenomena of motions to investigate the forces of Nature, and then from these forces to demonstrate the other phenomena ...

The Principia deals primarily with massive bodies in motion, initially under a variety of conditions and hypothetical laws of force in both non-resisting and resisting media, thus offering criteria to decide, by observations, which laws of force are operating in phenomena that may be observed. It attempts to cover hypothetical or possible motions both of celestial bodies and of terrestrial projectiles. It explores difficult problems of motions perturbed by multiple attractive forces. Its third and final book deals with the interpretation of observations about the movements of planets and their satellites.

The book:

shows how astronomical observations verify the inverse square law of gravitation (to an accuracy that was high by the standards of Newton's time);
offers estimates of relative masses for the known giant planets and for the Earth and the Sun;
defines the motion of the Sun relative to the Solar System barycenter;
shows how the theory of gravity can account for irregularities in the motion of the Moon;
identifies the oblateness of the shape of the Earth;
accounts approximately for marine tides including phenomena of spring and neap tides by the perturbing (and varying) gravitational attractions of the Sun and Moon on the Earth's waters;
explains the precession of the equinoxes as an effect of the gravitational attraction of the Moon on the Earth's equatorial bulge; and
gives theoretical basis for numerous phenomena about comets and their elongated, near-parabolic orbits.

The opening sections of the Principia contain, in revised and extended form, nearly^[14] all of the content of Newton's 1684 tract De motu corporum in gyrum.

The Principia begin with "Definitions"^[15] and "Axioms or Laws of Motion",^[16] and continues in three books:

Book 1, De motu corporum[edit]

Book 1, subtitled De motu corporum (On the motion of bodies) concerns motion in the absence of any resisting medium. It opens with a collection of mathematical lemmas on "the method of first and last ratios",^[17] a geometrical form of infinitesimal calculus.^[8]

The second section establishes relationships between centripetal forces and the law of areas now known as Kepler's second law (Propositions 1–3),^[18] and relates circular velocity and radius of path-curvature to radial force^[19] (Proposition 4), and relationships between centripetal forces varying as the inverse-square of the distance to the center and orbits of conic-section form (Propositions 5–10).

Propositions 11–31^[20] establish properties of motion in paths of eccentric conic-section form including ellipses, and their relationship with inverse-square central forces directed to a focus and include Newton's theorem about ovals (lemma 28).

Propositions 43–45^[21] are demonstration that in an eccentric orbit under centripetal force where the apse may move, a steady non-moving orientation of the line of apses is an indicator of an inverse-square law of force.

Book 1 contains some proofs with little connection to real-world dynamics. But there are also sections with far-reaching application to the solar system and universe:

Propositions 57–69^[22] deal with the "motion of bodies drawn to one another by centripetal forces". This section is of primary interest for its application to the Solar System, and includes Proposition 66^[23] along with its 22 corollaries:^[24] here Newton took the first steps in the definition and study of the problem of the movements of three massive bodies subject to their mutually perturbing gravitational attractions, a problem which later gained name and fame (among other reasons, for its great difficulty) as the three-body problem.

Propositions 70–84^[25] deal with the attractive forces of spherical bodies. The section contains Newton's proof that a massive spherically symmetrical body attracts other bodies outside itself as if all its mass were concentrated at its centre. This fundamental result, called the Shell theorem, enables the inverse square law of gravitation to be applied to the real solar system to a very close degree of approximation.

Book 2, part 2 of De motu corporum[edit]

Part of the contents originally planned for the first book was divided out into a second book, which largely concerns motion through resisting mediums. Just as Newton examined consequences of different conceivable laws of attraction in Book 1, here he examines different conceivable laws of resistance; thus Section 1 discusses resistance in direct proportion to velocity, and Section 2 goes on to examine the implications of resistance in proportion to the square of velocity. Book 2 also discusses (in Section 5) hydrostatics and the properties of compressible fluids; Newton also derives Boyle's law.^[26] The effects of air resistance on pendulums are studied in Section 6, along with Newton's account of experiments that he carried out, to try to find out some characteristics of air resistance in reality by observing the motions of pendulums under different conditions. Newton compares the resistance offered by a medium against motions of globes with different properties (material, weight, size). In Section 8, he derives rules to determine the speed of waves in fluids and relates them to the density and condensation (Proposition 48;^[27] this would become very important in acoustics). He assumes that these rules apply equally to light and sound and estimates that the speed of sound is around 1088 feet per second and can increase depending on the amount of water in air.^[28]

Less of Book 2 has stood the test of time than of Books 1 and 3, and it has been said that Book 2 was largely written to refute a theory of Descarteswhich had some wide acceptance before Newton's work (and for some time after). According to Descartes's theory of vortices, planetary motions were produced by the whirling of fluid vortices that filled interplanetary space and carried the planets along with them.^[29] Newton concluded Book 2^[30] by commenting that the hypothesis of vortices was completely at odds with the astronomical phenomena, and served not so much to explain as to confuse them.

Book 3, De mundi systemate[edit]

Book 3, subtitled De mundi systemate (On the system of the world), is an exposition of many consequences of universal gravitation, especially its consequences for astronomy. It builds upon the propositions of the previous books and applies them with further specificity than in Book 1 to the motions observed in the Solar System. Here (introduced by Proposition 22,^[31] and continuing in Propositions 25–35^[32]) are developed several of the features and irregularities of the orbital motion of the Moon, especially the variation. Newton lists the astronomical observations on which he relies,^[33] and establishes in a stepwise manner that the inverse square law of mutual gravitation applies to Solar System bodies, starting with the satellites of Jupiter^[34]and going on by stages to show that the law is of universal application.^[35] He also gives starting at Lemma 4^[36] and Proposition 40^[37] the theory of the motions of comets, for which much data came from John Flamsteed and Edmond Halley, and accounts for the tides,^[38] attempting quantitative estimates of the contributions of the Sun^[39] and Moon^[40] to the tidal motions; and offers the first theory of the precession of the equinoxes.^[41] Book 3 also considers the harmonic oscillator in three dimensions, and motion in arbitrary force laws.

In Book 3 Newton also made clear his heliocentric view of the Solar System, modified in a somewhat modern way, since already in the mid-1680s he recognised the "deviation of the Sun" from the centre of gravity of the Solar System.^[42] For Newton, "the common centre of gravity of the Earth, the Sun and all the Planets is to be esteem'd the Centre of the World",^[43] and that this centre "either is at rest, or moves uniformly forward in a right line".^[44]Newton rejected the second alternative after adopting the position that "the centre of the system of the world is immoveable", which "is acknowledg'd by all, while some contend that the Earth, others, that the Sun is fix'd in that centre".^[44] Newton estimated the mass ratios Sun:Jupiter and Sun:Saturn,^[45]and pointed out that these put the centre of the Sun usually a little way off the common center of gravity, but only a little, the distance at most "would scarcely amount to one diameter of the Sun".^[46]

Commentary on the Principia[edit]

The sequence of definitions used in setting up dynamics in the Principia is recognisable in many textbooks today. Newton first set out the definition of mass

The quantity of matter is that which arises conjointly from its density and magnitude. A body twice as dense in double the space is quadruple in quantity. This quantity I designate by the name of body or of mass.

This was then used to define the "quantity of motion" (today called momentum), and the principle of inertia in which mass replaces the previous Cartesian notion of intrinsic force. This then set the stage for the introduction of forces through the change in momentum of a body. Curiously, for today's readers, the exposition looks dimensionally incorrect, since Newton does not introduce the dimension of time in rates of changes of quantities.

He defined space and time "not as they are well known to all". Instead, he defined "true" time and space as "absolute"^[47] and explained:

Only I must observe, that the vulgar conceive those quantities under no other notions but from the relation they bear to perceptible objects. And it will be convenient to distinguish them into absolute and relative, true and apparent, mathematical and common. ... instead of absolute places and motions, we use relative ones; and that without any inconvenience in common affairs; but in philosophical discussions, we ought to step back from our senses, and consider things themselves, distinct from what are only perceptible measures of them.

To some modern readers it can appear that some dynamical quantities recognised today were used in the Principia but not named. The mathematical aspects of the first two books were so clearly consistent that they were easily accepted; for example, Locke asked Huygens whether he could trust the mathematical proofs and was assured about their correctness.

However, the concept of an attractive force acting at a distance received a cooler response. In his notes, Newton wrote that the inverse square law arose naturally due to the structure of matter. However, he retracted this sentence in the published version, where he stated that the motion of planets is consistent with an inverse square law, but refused to speculate on the origin of the law. Huygens and Leibniz noted that the law was incompatible with the notion of the aether. From a Cartesian point of view, therefore, this was a faulty theory. Newton's defence has been adopted since by many famous physicists—he pointed out that the mathematical form of the theory had to be correct since it explained the data, and he refused to speculate further on the basic nature of gravity. The sheer number of phenomena that could be organised by the theory was so impressive that younger "philosophers" soon adopted the methods and language of the Principia.

Rules of Reason[edit]

Perhaps to reduce the risk of public misunderstanding, Newton included at the beginning of Book 3 (in the second (1713) and third (1726) editions) a section titled "Rules of Reasoning in Philosophy". In the four rules, as they came finally to stand in the 1726 edition, Newton effectively offers a methodology for handling unknown phenomena in nature and reaching towards explanations for them. The four Rules of the 1726 edition run as follows (omitting some explanatory comments that follow each):

We are to admit no more causes of natural things than such as are both true and sufficient to explain their appearances.
Therefore to the same natural effects we must, as far as possible, assign the same causes.
The qualities of bodies, which admit neither intensification nor remission of degrees, and which are found to belong to all bodies within the reach of our experiments, are to be esteemed the universal qualities of all bodies whatsoever.
In experimental philosophy we are to look upon propositions inferred by general induction from phenomena as accurately or very nearly true, not withstanding any contrary hypothesis that may be imagined, till such time as other phenomena occur, by which they may either be made more accurate, or liable to exceptions.

This section of Rules for philosophy is followed by a listing of "Phenomena", in which are listed a number of mainly astronomical observations, that Newton used as the basis for inferences later on, as if adopting a consensus set of facts from the astronomers of his time.

Both the "Rules" and the "Phenomena" evolved from one edition of the Principia to the next. Rule 4 made its appearance in the third (1726) edition; Rules 1–3 were present as "Rules" in the second (1713) edition, and predecessors of them were also present in the first edition of 1687, but there they had a different heading: they were not given as "Rules", but rather in the first (1687) edition the predecessors of the three later "Rules", and of most of the later "Phenomena", were all lumped together under a single heading "Hypotheses" (in which the third item was the predecessor of a heavy revision that gave the later Rule 3).

From this textual evolution, it appears that Newton wanted by the later headings "Rules" and "Phenomena" to clarify for his readers his view of the roles to be played by these various statements.

In the third (1726) edition of the Principia, Newton explains each rule in an alternative way and/or gives an example to back up what the rule is claiming. The first rule is explained as a philosophers' principle of economy. The second rule states that if one cause is assigned to a natural effect, then the same cause so far as possible must be assigned to natural effects of the same kind: for example, respiration in humans and in animals, fires in the home and in the Sun, or the reflection of light whether it occurs terrestrially or from the planets. An extensive explanation is given of the third rule, concerning the qualities of bodies, and Newton discusses here the generalisation of observational results, with a caution against making up fancies contrary to experiments, and use of the rules to illustrate the observation of gravity and space.

General Scholium[edit]

The General Scholium is a concluding essay added to the second edition, 1713 (and amended in the third edition, 1726).^[48] It is not to be confused with the General Scholium at the end of Book 2, Section 6, which discusses his pendulum experiments and resistance due to air, water, and other fluids.

Here Newton used the expression hypotheses non fingo, "I formulate no hypotheses",^[9] in response to criticisms of the first edition of the Principia. ("Fingo" is sometimes nowadays translated "feign" rather than the traditional "frame," although "feign" does not properly translate "fingo"). Newton's gravitational attraction, an invisible force able to act over vast distances, had led to criticism that he had introduced "occult agencies" into science.^[49]Newton firmly rejected such criticisms and wrote that it was enough that the phenomena implied gravitational attraction, as they did; but the phenomena did not so far indicate the cause of this gravity, and it was both unnecessary and improper to frame hypotheses of things not implied by the phenomena: such hypotheses "have no place in experimental philosophy", in contrast to the proper way in which "particular propositions are inferr'd from the phenomena and afterwards rendered general by induction".^[50]

Newton also underlined his criticism of the vortex theory of planetary motions, of Descartes, pointing to its incompatibility with the highly eccentric orbits of comets, which carry them "through all parts of the heavens indifferently".

Newton also gave theological argument. From the system of the world, he inferred the existence of a god, along lines similar to what is sometimes called the argument from intelligent or purposive design. It has been suggested that Newton gave "an oblique argument for a unitarian conception of God and an implicit attack on the doctrine of the Trinity".^[51]^[52] The General Scholium does not address or attempt to refute the church doctrine; it simply does not mention Jesus, the Holy Ghost, or the hypothesis of the Trinity.

Publishing the book[edit]

Halley and Newton's initial stimulus[edit]

In January 1684, Edmond Halley, Christopher Wren and Robert Hooke had a conversation in which Hooke claimed to not only have derived the inverse-square law but also all the laws of planetary motion. Wren was unconvinced, Hooke did not produce the claimed derivation although the others gave him time to do it, and Halley, who could derive the inverse-square law for the restricted circular case (by substituting Kepler's relation into Huygens' formula for the centrifugal force) but failed to derive the relation generally, resolved to ask Newton.^[53]

Halley's visits to Newton in 1684 thus resulted from Halley's debates about planetary motion with Wren and Hooke, and they seem to have provided Newton with the incentive and spur to develop and write what became Philosophiae Naturalis Principia Mathematica. Halley was at that time a Fellow and Council member of the Royal Society in London (positions that in 1686 he resigned to become the Society's paid Clerk).^[54] Halley's visit to Newton in Cambridge in 1684 probably occurred in August.^[55] When Halley asked Newton's opinion on the problem of planetary motions discussed earlier that year between Halley, Hooke and Wren,^[56] Newton surprised Halley by saying that he had already made the derivations some time ago; but that he could not find the papers. (Matching accounts of this meeting come from Halley and Abraham De Moivre to whom Newton confided.) Halley then had to wait for Newton to "find" the results, and in November 1684 Newton sent Halley an amplified version of whatever previous work Newton had done on the subject. This took the form of a 9-page manuscript, De motu corporum in gyrum (Of the motion of bodies in an orbit): the title is shown on some surviving copies, although the (lost) original may have been without a title.

Newton's tract De motu corporum in gyrum, which he sent to Halley in late 1684, derived what is now known as the three laws of Kepler, assuming an inverse square law of force, and generalised the result to conic sections. It also extended the methodology by adding the solution of a problem on the motion of a body through a resisting medium. The contents of De motu so excited Halley by their mathematical and physical originality and far-reaching implications for astronomical theory, that he immediately went to visit Newton again, in November 1684, to ask Newton to let the Royal Society have more of such work.^[57] The results of their meetings clearly helped to stimulate Newton with the enthusiasm needed to take his investigations of mathematical problems much further in this area of physical science, and he did so in a period of highly concentrated work that lasted at least until mid-1686.^[58]

Newton's single-minded attention to his work generally, and to his project during this time, is shown by later reminiscences from his secretary and copyist of the period, Humphrey Newton. His account tells of Isaac Newton's absorption in his studies, how he sometimes forgot his food, or his sleep, or the state of his clothes, and how when he took a walk in his garden he would sometimes rush back to his room with some new thought, not even waiting to sit before beginning to write it down.^[59] Other evidence also shows Newton's absorption in the Principia: Newton for years kept up a regular programme of chemical or alchemical experiments, and he normally kept dated notes of them, but for a period from May 1684 to April 1686, Newton's chemical notebooks have no entries at all.^[60] So, it seems that Newton abandoned pursuits to which he was formally dedicated and did very little else for well over a year and a half, but concentrated on developing and writing what became his great work.

The first of the three constituent books was sent to Halley for the printer in spring 1686, and the other two books somewhat later. The complete work, published by Halley at his own financial risk,^[61] appeared in July 1687. Newton had also communicated De motu to Flamsteed, and during the period of composition, he exchanged a few letters with Flamsteed about observational data on the planets, eventually acknowledging Flamsteed's contributions in the published version of the Principia of 1687.

Preliminary version[edit]

Newton's own first edition copy of his *Principia*, with handwritten corrections for the second edition

The process of writing that first edition of the Principia went through several stages and drafts: some parts of the preliminary materials still survive, while others are lost except for fragments and cross-references in other documents.^[62]

Surviving materials show that Newton (up to some time in 1685) conceived his book as a two-volume work. The first volume was to be titled De motu corporum, Liber primus, with contents that later appeared in extended form as Book 1 of the Principia.^{[citation needed]}

A fair-copy draft of Newton's planned second volume De motu corporum, Liber Secundus survives, its completion dated to about the summer of 1685. It covers the application of the results of Liber primus to the Earth, the Moon, the tides, the Solar System, and the universe; in this respect, it has much the same purpose as the final Book 3 of the Principia, but it is written much less formally and is more easily read.^{[citation needed]}

It is not known just why Newton changed his mind so radically about the final form of what had been a readable narrative in De motu corporum, Liber Secundus of 1685, but he largely started afresh in a new, tighter, and less accessible mathematical style, eventually to produce Book 3 of the Principia as we know it. Newton frankly admitted that this change of style was deliberate when he wrote that he had (first) composed this book "in a popular method, that it might be read by many", but to "prevent the disputes" by readers who could not "lay aside the[ir] prejudices", he had "reduced" it "into the form of propositions (in the mathematical way) which should be read by those only, who had first made themselves masters of the principles established in the preceding books".^[63] The final Book 3 also contained in addition some further important quantitative results arrived at by Newton in the meantime, especially about the theory of the motions of comets, and some of the perturbations of the motions of the Moon.

The result was numbered Book 3 of the Principia rather than Book 2 because in the meantime, drafts of Liber primus had expanded and Newton had divided it into two books. The new and final Book 2 was concerned largely with the motions of bodies through resisting mediums.^[64]

But the Liber Secundus of 1685 can still be read today. Even after it was superseded by Book 3 of the Principia, it survived complete, in more than one manuscript. After Newton's death in 1727, the relatively accessible character of its writing encouraged the publication of an English translation in 1728 (by persons still unknown, not authorised by Newton's heirs). It appeared under the English title A Treatise of the System of the World.^[65] This had some amendments relative to Newton's manuscript of 1685, mostly to remove cross-references that used obsolete numbering to cite the propositions of an early draft of Book 1 of the Principia. Newton's heirs shortly afterwards published the Latin version in their possession, also in 1728, under the (new) title De Mundi Systemate, amended to update cross-references, citations and diagrams to those of the later editions of the Principia, making it look superficially as if it had been written by Newton after the Principia, rather than before.^[66] The System of the World was sufficiently popular to stimulate two revisions (with similar changes as in the Latin printing), a second edition (1731), and a "corrected" reprint^[67] of the second edition (1740).

Halley's role as publisher[edit]

The text of the first of the three books of the Principia was presented to the Royal Society at the close of April 1686. Hooke made some priority claims (but failed to substantiate them), causing some delay. When Hooke's claim was made known to Newton, who hated disputes, Newton threatened to withdraw and suppress Book 3 altogether, but Halley, showing considerable diplomatic skills, tactfully persuaded Newton to withdraw his threat and let it go forward to publication. Samuel Pepys, as president, gave his imprimatur on 30 June 1686, licensing the book for publication. The Society had just spent its book budget on De Historia piscium,^[68] and the cost of publication was borne by Edmund Halley (who was also then acting as publisher of the Philosophical Transactions of the Royal Society):^[69] the book appeared in summer 1687.^[70] After Halley had personally financed the publication of Principia, he was informed that the society could no longer afford to provide him the promised annual salary of £50. Instead, Halley was paid with leftover copies of De Historia piscium.^[71]

Historical context[edit]

Beginnings of the Scientific Revolution[edit]

Nicolaus Copernicus had moved the Earth away from the center of the universe with the heliocentric theory for which he presented evidence in his book De revolutionibus orbium coelestium (On the revolutions of the heavenly spheres) published in 1543. Johannes Kepler wrote the book Astronomia nova (A new astronomy) in 1609, setting out the evidence that planets move in elliptical orbits with the Sun at one focus, and that planets do not move with constant speed along this orbit. Rather, their speed varies so that the line joining the centres of the sun and a planet sweeps out equal areas in equal times. To these two laws he added a third a decade later, in his 1619 book Harmonices Mundi (Harmonies of the world). This law sets out a proportionality between the third power of the characteristic distance of a planet from the Sun and the square of the length of its year.

The foundation of modern dynamics was set out in Galileo's book Dialogo sopra i due massimi sistemi del mondo (Dialogue on the two main world systems) where the notion of inertia was implicit and used. In addition, Galileo's experiments with inclined planes had yielded precise mathematical relations between elapsed time and acceleration, velocity or distance for uniform and uniformly accelerated motion of bodies.

Descartes' book of 1644 Principia philosophiae (Principles of philosophy) stated that bodies can act on each other only through contact: a principle that induced people, among them himself, to hypothesize a universal medium as the carrier of interactions such as light and gravity—the aether. Newton was criticized for apparently introducing forces that acted at distance without any medium.^[49] Not until the development of particle theory was Descartes' notion vindicated when it was possible to describe all interactions, like the strong, weak, and electromagnetic fundamental interactions, using mediating gauge bosons^[72] and gravity through hypothesized gravitons.^[73]

Newton's role[edit]

Newton had studied these books, or, in some cases, secondary sources based on them, and taken notes entitled Quaestiones quaedam philosophicae (Questions about philosophy) during his days as an undergraduate. During this period (1664–1666) he created the basis of calculus and performed the first experiments in the optics of colour. At this time, his proof that white light was a combination of primary colours (found via prismatics) replaced the prevailing theory of colours and received an overwhelmingly favourable response and occasioned bitter disputes with Robert Hooke and others, which forced him to sharpen his ideas to the point where he already composed sections of his later book Opticks by the 1670s in response. Work on calculus is shown in various papers and letters, including two to Leibniz. He became a fellow of the Royal Society and the second Lucasian Professor of Mathematics (succeeding Isaac Barrow) at Trinity College, Cambridge.

Newton's early work on motion[edit]

In the 1660s Newton studied the motion of colliding bodies and deduced that the centre of mass of two colliding bodies remains in uniform motion. Surviving manuscripts of the 1660s also show Newton's interest in planetary motion and that by 1669 he had shown, for a circular case of planetary motion, that the force he called "endeavour to recede" (now called centrifugal force) had an inverse-square relation with distance from the center.^[74] After his 1679–1680 correspondence with Hooke, described below, Newton adopted the language of inward or centripetal force. According to Newton scholar J. Bruce Brackenridge, although much has been made of the change in language and difference of point of view, as between centrifugal or centripetal forces, the actual computations and proofs remained the same either way. They also involved the combination of tangential and radial displacements, which Newton was making in the 1660s. The difference between the centrifugal and centripetal points of view, though a significant change of perspective, did not change the analysis.^[75] Newton also clearly expressed the concept of linear inertia in the 1660s: for this Newton was indebted to Descartes' work published 1644.^[76]

Controversy with Hooke[edit]

Hooke published his ideas about gravitation in the 1660s and again in 1674. He argued for an attracting principle of gravitation in Micrographia of 1665, in a 1666 Royal Society lecture On gravity, and again in 1674, when he published his ideas about the System of the World in somewhat developed form, as an addition to An Attempt to Prove the Motion of the Earth from Observations.^[77] Hooke clearly postulated mutual attractions between the Sun and planets, in a way that increased with nearness to the attracting body, along with a principle of linear inertia. Hooke's statements up to 1674 made no mention, however, that an inverse square law applies or might apply to these attractions. Hooke's gravitation was also not yet universal, though it approached universality more closely than previous hypotheses.^[78] Hooke also did not provide accompanying evidence or mathematical demonstration. On these two aspects, Hooke stated in 1674: "Now what these several degrees [of gravitational attraction] are I have not yet experimentally verified" (indicating that he did not yet know what law the gravitation might follow); and as to his whole proposal: "This I only hint at present", "having my self many other things in hand which I would first compleat, and therefore cannot so well attend it" (i.e., "prosecuting this Inquiry").^[77]

In November 1679, Hooke began an exchange of letters with Newton, of which the full text is now published.^[79]Hooke told Newton that Hooke had been appointed to manage the Royal Society's correspondence,^[80] and wished to hear from members about their researches, or their views about the researches of others; and as if to whet Newton's interest, he asked what Newton thought about various matters, giving a whole list, mentioning "compounding the celestial motions of the planets of a direct motion by the tangent and an attractive motion towards the central body", and "my hypothesis of the lawes or causes of springinesse", and then a new hypothesis from Paris about planetary motions (which Hooke described at length), and then efforts to carry out or improve national surveys, the difference of latitude between London and Cambridge, and other items. Newton's reply offered "a fansy of my own" about a terrestrial experiment (not a proposal about celestial motions) which might detect the Earth's motion, by the use of a body first suspended in air and then dropped to let it fall. The main point was to indicate how Newton thought the falling body could experimentally reveal the Earth's motion by its direction of deviation from the vertical, but he went on hypothetically to consider how its motion could continue if the solid Earth had not been in the way (on a spiral path to the centre). Hooke disagreed with Newton's idea of how the body would continue to move.^[81] A short further correspondence developed, and towards the end of it Hooke, writing on 6 January 1680 to Newton, communicated his "supposition ... that the Attraction always is in a duplicate proportion to the Distance from the Center Reciprocall, and Consequently that the Velocity will be in a subduplicate proportion to the Attraction and Consequently as Kepler Supposes Reciprocall to the Distance."^[82] (Hooke's inference about the velocity was actually incorrect.^[83])

In 1686, when the first book of Newton's Principia was presented to the Royal Society, Hooke claimed that Newton had obtained from him the "notion" of "the rule of the decrease of Gravity, being reciprocally as the squares of the distances from the Center". At the same time (according to Edmond Halley's contemporary report) Hooke agreed that "the Demonstration of the Curves generated therby" was wholly Newton's.^[79]

A recent assessment about the early history of the inverse square law is that "by the late 1660s", the assumption of an "inverse proportion between gravity and the square of distance was rather common and had been advanced by a number of different people for different reasons".^[84] Newton himself had shown in the 1660s that for planetary motion under a circular assumption, force in the radial direction had an inverse-square relation with distance from the center.^[74] Newton, faced in May 1686 with Hooke's claim on the inverse square law, denied that Hooke was to be credited as author of the idea, giving reasons including the citation of prior work by others before Hooke.^[79] Newton also firmly claimed that even if it had happened that he had first heard of the inverse square proportion from Hooke, which it had not, he would still have some rights to it in view of his mathematical developments and demonstrations, which enabled observations to be relied on as evidence of its accuracy, while Hooke, without mathematical demonstrations and evidence in favour of the supposition, could only guess (according to Newton) that it was approximately valid "at great distances from the center".^[79]

The background described above shows there was basis for Newton to deny deriving the inverse square law from Hooke. On the other hand, Newton did accept and acknowledge, in all editions of the Principia, that Hooke (but not exclusively Hooke) had separately appreciated the inverse square law in the Solar System. Newton acknowledged Wren, Hooke and Halley in this connection in the Scholium to Proposition 4 in Book 1.^[85] Newton also acknowledged to Halley that his correspondence with Hooke in 1679–80 had reawakened his dormant interest in astronomical matters, but that did not mean, according to Newton, that Hooke had told Newton anything new or original: "yet am I not beholden to him for any light into that business but only for the diversion he gave me from my other studies to think on these things & for his dogmaticalness in writing as if he had found the motion in the Ellipsis, which inclined me to try it ...".^[79]) Newton's reawakening interest in astronomy received further stimulus by the appearance of a comet in the winter of 1680/1681, on which he corresponded with John Flamsteed.^[86]

In 1759, decades after the deaths of both Newton and Hooke, Alexis Clairaut, mathematical astronomer eminent in his own right in the field of gravitational studies, made his assessment after reviewing what Hooke had published on gravitation. "One must not think that this idea ... of Hooke diminishes Newton's glory", Clairaut wrote; "The example of Hooke" serves "to show what a distance there is between a truth that is glimpsed and a truth that is demonstrated".^[87]^[88]

Location of early edition copies[edit]

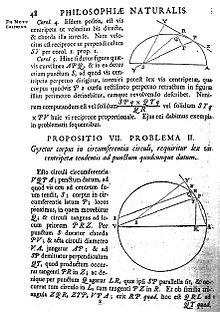
It has been estimated that as many as 750 copies^[89] of the first edition were printed by the Royal Society, and "it is quite remarkable that so many copies of this small first edition are still in existence ... but it may be because the original Latin text was more revered than read".^[90] A survey published in 1953 located 189 surviving copies^[91] with nearly 200 further copies located by the most recent survey published in 2020, suggesting that the initial print run was larger than previously thought.^[92] However, more recent book historical and bibliographical research has examined those prior claims, and concludes that Macomber's earlier estimation of 500 copies is likely correct.^[93]

Cambridge University Library has Newton's own copy of the first edition, with handwritten notes for the second edition.^[94]
The Earl Gregg Swem Library at the College of William & Mary has a first edition copy of the Principia.^[95]Throughout are Latin annotations written by Thomas S. Savage. These handwritten notes are currently being researched at the college.^[96]
The Frederick E. Brasch Collection of Newton and Newtoniana in Stanford University also has a first edition of the Principia.^[97]
A first edition forms part of the Crawford Collection, housed at the Royal Observatory, Edinburgh.^[98]
The Uppsala University Library owns a first edition copy, which was stolen in the 1960s and returned to the library in 2009.^[99]
The Folger Shakespeare Library in Washington, D.C. owns a first edition, as well as a 1713 second edition.
The Huntington Library in San Marino, California owns Isaac Newton's personal copy, with annotations in Newton's own hand.^[100]
The Bodmer Library in Switzerland keeps a copy of the original edition that was owned by Leibniz. It contains handwritten notes by Leibniz, in particular concerning the controversy of who first formulated calculus (although he published it later, Newton argued that he developed it earlier).^[101]
The Iron Library in Switzerland holds a first edition copy that was formerly in the library of the physicist Ernst Mach. The copy contains critical marginalia in Mach's hand.^[102]
The University of St Andrews Library holds both variants of the first edition, as well as copies of the 1713 and 1726 editions.^[103]
The Fisher Library in the University of Sydney has a first-edition copy, annotated by a mathematician of uncertain identity and corresponding notes from Newton himself.^[104]
The Linda Hall Library holds the first edition, as well as a copy of the 1713 and 1726 editions.
The Teleki-Bolyai Library of Târgu-Mureș holds a 2-line imprint first edition.
One book is also located at Vasaskolan, Gävle, in Sweden.^[105]
Dalhousie University has a copy as part of the William I. Morse collection.
McGill University in Montreal has the copy once owned by Sir William Osler.
The University of Toronto has a copy in the Thomas Fisher Rare Book Collection.
University College London Special Collections has a copy previously owned by the lawyer and mathematician John T. Graves.^[106]

In 2016, a first edition sold for $3.7 million.^[107]

The second edition (1713) were printed in 750 copies, and the third edition (1726) were printed in 1,250 copies.

A facsimile edition (based on the 3rd edition of 1726 but with variant readings from earlier editions and important annotations) was published in 1972 by Alexandre Koyré and I. Bernard Cohen.^[11]

Later editions[edit]

Second edition, 1713[edit]

Two later editions were published by Newton: Newton had been urged to make a new edition of the Principiasince the early 1690s, partly because copies of the first edition had already become very rare and expensive within a few years after 1687.^[108] Newton referred to his plans for a second edition in correspondence with Flamsteed in November 1694.^[109] Newton also maintained annotated copies of the first edition specially bound up with interleaves on which he could note his revisions; two of these copies still survive,^[110] but he had not completed the revisions by 1708. Newton had almost severed connections with one would-be editor, Nicolas Fatio de Duillier, and another, David Gregory seems not to have met with his approval and was also terminally ill, dying in 1708. Nevertheless, reasons were accumulating not to put off the new edition any longer.^[111] Richard Bentley, master of Trinity College, persuaded Newton to allow him to undertake a second edition, and in June 1708 Bentley wrote to Newton with a specimen print of the first sheet, at the same time expressing the (unfulfilled) hope that Newton had made progress towards finishing the revisions.^[112] It seems that Bentley then realised that the editorship was technically too difficult for him, and with Newton's consent he appointed Roger Cotes, Plumian professor of astronomy at Trinity, to undertake the editorship for him as a kind of deputy (but Bentley still made the publishing arrangements and had the financial responsibility and profit). The correspondence of 1709–1713 shows Cotes reporting to two masters, Bentley and Newton, and managing (and often correcting) a large and important set of revisions to which Newton sometimes could not give his full attention.^[113] Under the weight of Cotes' efforts, but impeded by priority disputes between Newton and Leibniz,^[114] and by troubles at the Mint,^[115] Cotes was able to announce publication to Newton on 30 June 1713.^[116] Bentley sent Newton only six presentation copies; Cotes was unpaid; Newton omitted any acknowledgement to Cotes.

Among those who gave Newton corrections for the Second Edition were: Firmin Abauzit, Roger Cotes and David Gregory. However, Newton omitted acknowledgements to some because of the priority disputes. John Flamsteed, the Astronomer Royal, suffered this especially.

The Second Edition was the basis of the first edition to be printed abroad, which appeared in Amsterdam in 1714.

Third edition, 1726[edit]

After his serious illness in 1722 and after the appearance of a reprint of the second edition in Amsterdam in 1723, the 80-year-old Newton began to revise once again the Principia in the fall of 1723. The third edition was published 25 March 1726, under the stewardship of Henry Pemberton, M.D., a man of the greatest skill in these matters...; Pemberton later said that this recognition was worth more to him than the two hundred guinea award from Newton.^[117]

In 1739–1742, two French priests, Pères Thomas LeSeur and François Jacquier (of the Minim order, but sometimes erroneously identified as Jesuits), produced with the assistance of J.-L. Calandrini an extensively annotated version of the Principia in the 3rd edition of 1726. Sometimes this is referred to as the Jesuit edition: it was much used, and reprinted more than once in Scotland during the 19th century.^[118]

Émilie du Châtelet also made a translation of Newton's Principia into French. Unlike LeSeur and Jacquier's edition, hers was a complete translation of Newton's three books and their prefaces. She also included a Commentary section where she fused the three books into a much clearer and easier to understand summary. She included an analytical section where she applied the new mathematics of calculus to Newton's most controversial theories. Previously, geometry was the standard mathematics used to analyse theories. Du Châtelet's translation is the only complete one to have been done in French and hers remains the standard French translation to this day.^[119]

Translations[edit]

Title page to a 1848 copy of The Mathematical Principles of Natural Philosophy, translated into English by Andrew Motte — Title page to an 1848 copy of *The Mathematical Principles of Natural Philosophy*, translated into English by Andrew Motte

Four full English translations of Newton's Principia have appeared, all based on Newton's 3rd edition of 1726. The first, from 1729, by Andrew Motte,^[3] was described by Newton scholar I. Bernard Cohen (in 1968) as "still of enormous value in conveying to us the sense of Newton's words in their own time, and it is generally faithful to the original: clear, and well written".^[120] The 1729 version was the basis for several republications, often incorporating revisions, among them a widely used modernised English version of 1934, which appeared under the editorial name of Florian Cajori (though completed and published only some years after his death). Cohen pointed out ways in which the 18th-century terminology and punctuation of the 1729 translation might be confusing to modern readers, but he also made severe criticisms of the 1934 modernised English version, and showed that the revisions had been made without regard to the original, also demonstrating gross errors "that provided the final impetus to our decision to produce a wholly new translation".^[121]

The second full English translation, into modern English, is the work that resulted from this decision by collaborating translators I. Bernard Cohen, Anne Whitman, and Julia Budenz; it was published in 1999 with a guide by way of introduction.^[122]

The third such translation is due to Ian Bruce, and appears, with many other translations of mathematical works of the 17th and 18th centuries, on his website.^[123]

The fourth complete English translation is due to Charles Leedham-Green, professor emeritus of mathematics at Queen Mary University of London, and was published in 2021 by Cambridge University Press.^[124] Prof. Leedham-Green was motivated to produce that translation, on which he worked for twenty years, in part because of his dissatisfaction with the work of Cohen, Whitman, and Budenz, whose translation of the Principia he found unnecessarily obscure. Leedham-Green's aim was to convey Newton's own reasoning and arguments in a way intelligible to a modern mathematical scientist. His translation is heavily annotated and his explanatory notes make use of the modern secondary literature on some of the more difficult technical aspects of Newton's work.

Dana Densmore and William H. Donahue have published a translation of the work's central argument, published in 1996, along with expansion of included proofs and ample commentary.^[125] The book was developed as a textbook for classes at St. John's College and the aim of this translation is to be faithful to the Latin text.^[126]

Varia[edit]

In 1977, the spacecraft Voyager 1 and 2 left earth for the interstellar space carrying a picture of a page from Newton's Principia Mathematica, as part of the Golden Record, a collection of messages from humanity to extraterrestrials.

In 2014, British astronaut Tim Peake named his upcoming mission to the International Space Station Principiaafter the book, in "honour of Britain's greatest scientist".^[127] Tim Peake's Principia launched on 15 December 2015 aboard Soyuz TMA-19M.^[128]

Hi, where are you from?

Saturday, June 1, 2024

You searched for

"WONDERING" in the KJV Bible