Oh For Those Infinite Numbers That Add To A Natural Series!!

Carl Friedrich Gauss

From Wikipedia, the free encyclopedia

"Gauss" redirects here. For other persons or things named Gauss, see Gauss (disambiguation).

Carl Friedrich Gauss
Carl Friedrich Gauß (1777–1855), painted by Christian Albrecht Jensen
Born	Johann Carl Friedrich Gauss 30 April 1777 Brunswick, Principality of Brunswick-Wolfenbüttel, Holy Roman Empire
Died	23 February 1855 (aged 77) Göttingen, Kingdom of Hanover
Residence	Kingdom of Hanover
Nationality	German
Alma mater	Collegium Carolinum, University of Göttingen, University of Helmstedt
Known for	See full list
Awards	Lalande Prize (1810) Copley Medal (1838)
Scientific career
Fields	Mathematics and physics
Institutions	University of Göttingen
Thesis	Demonstratio nova... (1799)
Doctoral advisor	Johann Friedrich Pfaff
Other academic advisors	Johann Christian Martin Bartels
Doctoral students	Johann Listing Christian Ludwig Gerling Richard Dedekind Bernhard Riemann Christian Peters Moritz Cantor
Other notable students	Johann Encke Christoph Gudermann Peter Gustav Lejeune Dirichlet Gotthold Eisenstein Carl Wolfgang Benjamin Goldschmidt Gustav Kirchhoff Ernst Kummer August Ferdinand Möbius L. C. Schnürlein Julius Weisbach Friedrich Bessel (epistolary correspondent) Sophie Germain (epistolary correspondent)
Influenced	Ferdinand Minding
Signature

Johann Carl Friedrich Gauss (/ɡaʊs/; German: Gauß [ɡaʊs] ( listen); Latin: Carolus Fridericus Gauss; 30 April 1777 – 23 February 1855) was a German mathematician who made significant contributions to many fields, including number theory, algebra, statistics, analysis, differential geometry, geodesy, geophysics, mechanics, electrostatics, magnetic fields, astronomy, matrix theory, and optics.
Sometimes referred to as the Princeps mathematicorum^[1] (Latin for "the foremost of mathematicians") and "the greatest mathematician since antiquity", Gauss had an exceptional influence in many fields of mathematics and science, and is ranked among history's most influential mathematicians.^[2]

Contents

• 1 Personal life
  • 1.1 Early years
  • 1.2 Marriage and children
  • 1.3 Later years and death
  • 1.4 Religious views
  • 1.5 Family
  • 1.6 Personality
• 2 Careers and achievements
  • 2.1 Algebra
  • 2.2 Astronomy
  • 2.3 Geodetic survey
  • 2.4 Non-Euclidean geometries
  • 2.5 Theorema Egregium
• 3 Appraisal of Gauss
• 4 Anecdotes
• 5 Commemorations
• 6 Writings
• 7 See also
• 8 Notes
• 9 Further reading
• 10 External links

Personal life

Early years

Statue of Gauss at his birthplace, Brunswick

Johann Carl Friedrich Gauss was born on 30 April 1777 in Brunswick (Braunschweig), in the Duchy of Brunswick-Wolfenbüttel (now part of Lower Saxony, Germany), to poor, working-class parents.^[3] His mother was illiterate and never recorded the date of his birth, remembering only that he had been born on a Wednesday, eight days before the Feast of the Ascension (which occurs 39 days after Easter). Gauss later solved this puzzle about his birthdate in the context of finding the date of Easter, deriving methods to compute the date in both past and future years.^[4] He was christened and confirmed in a church near the school he attended as a child.^[5]
Gauss was a child prodigy. A contested story relates that, when he was eight, he figured out how to add up all the numbers from 1 to 100.^[6][7][8]. . . . . read more at * or https://en.wikipedia.org/wiki/Carl_Friedrich_Gauss as I will enjoy the moment spoken of "when he was eight, he figured out how to add up all the numbers from 1 to 100".

1 + 2 + 3 + 4 + ⋯

From Wikipedia, the free encyclopedia

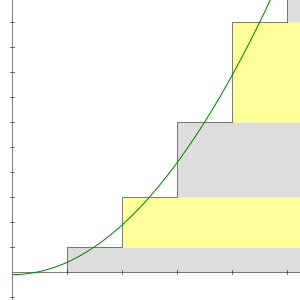
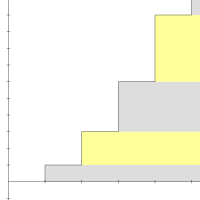
The first four partial sums of the series 1 + 2 + 3 + 4 + ⋯. The parabola is their smoothed asymptote; its y-intercept is − 1/12.^[1]

The infinite series whose terms are the natural numbers 1 + 2 + 3 + 4 + ⋯ is a divergent series. The nth partial sum of the series is the triangular number

${\displaystyle \sum _{k=1}^{n}k={\frac {n(n+1)}{2}},}$

which increases without bound as n goes to infinity. Because the sequence of partial sums fails to converge to a finite limit, the series does not have a sum.
Although the series seems at first sight not to have any meaningful value at all, it can be manipulated to yield a number of mathematically interesting results, some of which have applications in other fields such as complex analysis^{[citation needed]}, quantum field theory^{[citation needed]}, and string theory. Many summation methods are used in mathematics to assign numerical values even to a divergent series. In particular, the methods of zeta function regularization and Ramanujan summation assign the series a value of − 1/12, which is expressed by a famous formula:^[2]

${\displaystyle 1+2+3+4+\cdots =-{\frac {1}{12}},}$

where the left-hand side has to be interpreted as being the value obtained by using one of the aforementioned summation methods and not as the sum of an infinite series in its usual meaning.
In a monograph on moonshine theory, Terry Gannon calls this equation "one of the most remarkable formulae in science".^[3]

Partial sums

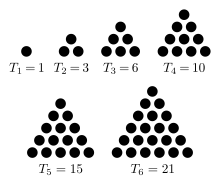
The first six triangular numbers

Main article: Triangular number

The partial sums of the series 1 + 2 + 3 + 4 + 5 + 6 + ⋯ are 1, 3, 6, 10, 15, etc. The nth partial sum is given by a simple formula:

${\displaystyle \sum _{k=1}^{n}k={\frac {n(n+1)}{2}}.}$

This equation was known to the Pythagoreans as early as the sixth century BCE.^[4] Numbers of this form are called triangular numbers, because they can be arranged as an equilateral triangle.
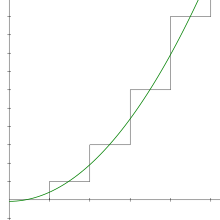
The infinite sequence of triangular numbers diverges to +∞, so by definition, the infinite series 1 + 2 + 3 + 4 + ⋯ also diverges to +∞. The divergence is a simple consequence of the form of the series: the terms do not approach zero, so the series diverges by the term test.

Summability

Among the classical divergent series, 1 + 2 + 3 + 4 + ⋯ is relatively difficult to manipulate into a finite value. Many summation methods are used to assign numerical values to divergent series, some more powerful than others. For example, Cesàro summation is a well-known method that sums Grandi's series, the mildly divergent series 1 − 1 + 1 − 1 + ⋯, to ​¹⁄₂. Abel summation is a more powerful method that not only sums Grandi's series to ​¹⁄₂, but also sums the trickier series 1 − 2 + 3 − 4 + ⋯ to ​¹⁄₄.
Unlike the above series, 1 + 2 + 3 + 4 + ⋯ is not Cesàro summable nor Abel summable. Those methods work on oscillating divergent series, but they cannot produce a finite answer for a series that diverges to +∞.^[5] Most of the more elementary definitions of the sum of a divergent series are stable and linear, and any method that is both stable and linear cannot sum 1 + 2 + 3 + ⋯ to a finite value; see below. More advanced methods are required, such as zeta function regularization or Ramanujan summation. It is also possible to argue for the value of − 1/12 using some rough heuristics related to these methods.

Heuristics

Passage from Ramanujan's first notebook describing the "constant" of the series

Srinivasa Ramanujan presented two derivations of "1 + 2 + 3 + 4 + ⋯ = − 1/12" in chapter 8 of his first notebook.^[6][7][8] The simpler, less rigorous derivation proceeds in two steps, as follows.
The first key insight is that the series of positive numbers 1 + 2 + 3 + 4 + ⋯ closely resembles the alternating series 1 − 2 + 3 − 4 + ⋯. The latter series is also divergent, but it is much easier to work with; there are several classical methods that assign it a value, which have been explored since the 18th century.^[9]
In order to transform the series 1 + 2 + 3 + 4 + ⋯ into 1 − 2 + 3 − 4 + ⋯, one can subtract 4 from the second term, 8 from the fourth term, 12 from the sixth term, and so on. The total amount to be subtracted is 4 + 8 + 12 + 16 + ⋯, which is 4 times the original series. These relationships can be expressed using algebra. Whatever the "sum" of the series might be, call it c = 1 + 2 + 3 + 4 + ⋯. Then multiply this equation by 4 and subtract the second equation from the first:

${\displaystyle {\begin{alignedat}{7}c&{}={}&1+2&&{}+3+4&&{}+5+6+\cdots \\4c&{}={}&4&&{}+8&&{}+12+\cdots \\c-4c&{}={}&1-2&&{}+3-4&&{}+5-6+\cdots \\\end{alignedat}}}$

The second key insight is that the alternating series 1 − 2 + 3 − 4 + ⋯ is the formal power series expansion of the function 1/(1 + x)² but with x defined as 1. Accordingly, Ramanujan writes:

${\displaystyle -3c=1-2+3-4+\cdots ={\frac {1}{(1+1)^{2}}}={\frac {1}{4}}}$

Dividing both sides by −3, one gets c = − 1/12.
Generally speaking, it is incorrect to manipulate infinite series as if they were finite sums. For example, if zeroes are inserted into arbitrary positions of a divergent series, it is possible to arrive at results that are not self-consistent, let alone consistent with other methods. In particular, the step 4c = 0 + 4 + 0 + 8 + ⋯ is not justified by the additive identity law alone. For an extreme example, appending a single zero to the front of the series can lead to inconsistent results.^[1]
One way to remedy this situation, and to constrain the places where zeroes may be inserted, is to keep track of each term in the series by attaching a dependence on some function.^[10] In the series 1 + 2 + 3 + 4 + ⋯, each term n is just a number. If the term n is promoted to a function n^−s, where s is a complex variable, then one can ensure that only like terms are added. The resulting series may be manipulated in a more rigorous fashion, and the variable s can be set to −1 later. The implementation of this strategy is called zeta function regularization.

Zeta function regularization

Plot of ζ(s). For s > 1, the series converges and ζ(s) > 1. Analytic continuation around the pole at s = 1 leads to a region of negative values, including ζ(−1) = − 1/12

In zeta function regularization, the series ${\displaystyle \sum _{n=1}^{\infty }n}$ is replaced by the series ${\displaystyle \sum _{n=1}^{\infty }n^{-s}}$. The latter series is an example of a Dirichlet series. When the real part of s is greater than 1, the Dirichlet series converges, and its sum is the Riemann zeta function ζ(s). On the other hand, the Dirichlet series diverges when the real part of s is less than or equal to 1, so, in particular, the series 1 + 2 + 3 + 4 + ⋯ that results from setting s = –1 does not converge. The benefit of introducing the Riemann zeta function is that it can be defined for other values of s by analytic continuation. One can then define the zeta-regularized sum of 1 + 2 + 3 + 4 + ⋯ to be ζ(−1).
From this point, there are a few ways to prove that ζ(−1) = − 1/12. One method, along the lines of Euler's reasoning,^[11] uses the relationship between the Riemann zeta function and the Dirichlet eta function η(s). The eta function is defined by an alternating Dirichlet series, so this method parallels the earlier heuristics. Where both Dirichlet series converge, one has the identities:

${\displaystyle {\begin{alignedat}{7}\zeta (s)&{}={}&1^{-s}+2^{-s}&&{}+3^{-s}+4^{-s}&&{}+5^{-s}+6^{-s}+\cdots &\\2\times 2^{-s}\zeta (s)&{}={}&2\times 2^{-s}&&{}+2\times 4^{-s}&&{}+2\times 6^{-s}+\cdots &\\\left(1-2^{1-s}\right)\zeta (s)&{}={}&1^{-s}-2^{-s}&&{}+3^{-s}-4^{-s}&&{}+5^{-s}-6^{-s}+\cdots &=\eta (s)\\\end{alignedat}}}$

The identity ${\displaystyle (1-2^{1-s})\zeta (s)=\eta (s)}$ continues to hold when both functions are extended by analytic continuation to include values of s for which the above series diverge. Substituting s = −1, one gets −3ζ(−1) = η(−1). Now, computing η(−1) is an easier task, as the eta function is equal to the Abel sum of its defining series,^[12] which is a one-sided limit:

${\displaystyle -3\zeta (-1)=\eta (-1)=\lim _{x\to 1^{-}}\left(1-2x+3x^{2}-4x^{3}+\cdots \right)=\lim _{x\to 1^{-}}{\frac {1}{(1+x)^{2}}}={\frac {1}{4}}}$

Dividing both sides by −3, one gets ζ(−1) = − 1/12.

Cutoff regularization

The series 1 + 2 + 3 + 4 + ⋯

After smoothing

Asymptotic behavior of the smoothing. The y-intercept of the parabola is − 1/12.^[1]

The method of regularization using a cutoff function can "smooth" the series to arrive at − 1/12. Smoothing is a conceptual bridge between zeta function regularization, with its reliance on complex analysis, and Ramanujan summation, with its shortcut to the Euler–Maclaurin formula. Instead, the method operates directly on conservative transformations of the series, using methods from real analysis.
The idea is to replace the ill-behaved discrete series ${\displaystyle \sum _{n=0}^{N}n}$ with a smoothed version

${\displaystyle \sum _{n=0}^{\infty }nf\left({\frac {n}{N}}\right)}$,

where f is a cutoff function with appropriate properties. The cutoff function must be normalized to f(0) = 1; this is a different normalization from the one used in differential equations. The cutoff function should have enough bounded derivatives to smooth out the wrinkles in the series, and it should decay to 0 faster than the series grows. For convenience, one may require that f is smooth, bounded, and compactly supported. One can then prove that this smoothed sum is asymptotic to − 1/12 + CN², where C is a constant that depends on f. The constant term of the asymptotic expansion does not depend on f: it is necessarily the same value given by analytic continuation, − 1/12.^[1]

Ramanujan summation

The Ramanujan sum of 1 + 2 + 3 + 4 + ⋯ is also − 1/12. Ramanujan wrote in his second letter to G. H. Hardy, dated 27 February 1913:

"Dear Sir, I am very much gratified on perusing your letter of the 8th February 1913. I was expecting a reply from you similar to the one which a Mathematics Professor at London wrote asking me to study carefully Bromwich's Infinite Series and not fall into the pitfalls of divergent series. … I told him that the sum of an infinite number of terms of the series: 1 + 2 + 3 + 4 + ⋯ = − 1/12 under my theory. If I tell you this you will at once point out to me the lunatic asylum as my goal. I dilate on this simply to convince you that you will not be able to follow my methods of proof if I indicate the lines on which I proceed in a single letter. …"^[13]

Ramanujan summation is a method to isolate the constant term in the Euler–Maclaurin formula for the partial sums of a series. For a function f, the classical Ramanujan sum of the series ${\displaystyle \sum _{k=1}^{\infty }f(k)}$ is defined as

${\displaystyle c=-{\frac {1}{2}}f(0)-\sum _{k=1}^{\infty }{\frac {B_{2k}}{(2k)!}}f^{(2k-1)}(0),}$

where f^(2k−1) is the (2k − 1)-th derivative of f and B_2k is the 2kth Bernoulli number: B₂ = 1/6, B₄ = − 1/30, and so on. Setting f(x) = x, the first derivative of f is 1, and every other term vanishes, so:^[14]

${\displaystyle c=-{\frac {1}{6}}\times {\frac {1}{2!}}=-{\frac {1}{12}}.}$

To avoid inconsistencies, the modern theory of Ramanujan summation requires that f is "regular" in the sense that the higher-order derivatives of f decay quickly enough for the remainder terms in the Euler–Maclaurin formula to tend to 0. Ramanujan tacitly assumed this property.^[14] The regularity requirement prevents the use of Ramanujan summation upon spaced-out series like 0 + 2 + 0 + 4 + ⋯, because no regular function takes those values. Instead, such a series must be interpreted by zeta function regularization. For this reason, Hardy recommends "great caution" when applying the Ramanujan sums of known series to find the sums of related series.^[15]

Failure of stable linear summation methods

This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (January 2015) (Learn how and when to remove this template message)

A summation method that is linear and stable cannot sum the series 1 + 2 + 3 + ⋯ to any finite value. (Stable means that adding a term to the beginning of the series increases the sum by the same amount.) This can be seen as follows. If

1 + 2 + 3 + ⋯ = x

then adding 0 to both sides gives

0 + 1 + 2 + ⋯ = 0 + x = x by stability.

By linearity, one may subtract the second equation from the first (subtracting each component of the second line from the first line in columns) to give

1 + 1 + 1 + ⋯ = x – x = 0.

Adding 0 to both sides again gives

0 + 1 + 1 + 1 + ⋯ = 0,

and subtracting the last two series gives

1 + 0 + 0 + ⋯ = 0

contradicting stability.
The methods used above to sum 1 + 2 + 3 + ⋯ are either not stable or not linear.

Physics

In bosonic string theory, the attempt is to compute the possible energy levels of a string, in particular the lowest energy level. Speaking informally, each harmonic of the string can be viewed as a collection of D − 2 independent quantum harmonic oscillators, one for each transverse direction, where D is the dimension of spacetime. If the fundamental oscillation frequency is ω then the energy in an oscillator contributing to the nth harmonic is nħω/2. So using the divergent series, the sum over all harmonics is − ħω(D − 2)/24. Ultimately it is this fact, combined with the Goddard–Thorn theorem, which leads to bosonic string theory failing to be consistent in dimensions other than 26.^[16]
The regularization of 1 + 2 + 3 + 4 + ⋯ is also involved in computing the Casimir force for a scalar field in one dimension.^[17] An exponential cutoff function suffices to smooth the series, representing the fact that arbitrarily high-energy modes are not blocked by the conducting plates. The spatial symmetry of the problem is responsible for canceling the quadratic term of the expansion. All that is left is the constant term − 1/12, and the negative sign of this result reflects the fact that the Casimir force is attractive.^[18]
A similar calculation is involved in three dimensions, using the Epstein zeta-function in place of the Riemann zeta function.^[19]

History

It is unclear whether Leonhard Euler summed the series to − 1/12. According to Morris Kline, Euler's early work on divergent series relied on function expansions, from which he concluded 1 + 2 + 3 + 4 + ⋯ = ∞.^[20] According to Raymond Ayoub, the fact that the divergent zeta series is not Abel summable prevented Euler from using the zeta function as freely as the eta function, and he "could not have attached a meaning" to the series.^[21] Other authors have credited Euler with the sum, suggesting that Euler would have extended the relationship between the zeta and eta functions to negative integers.^[22][23][24] In the primary literature, the series 1 + 2 + 3 + 4 + ⋯ is mentioned in Euler's 1760 publication De seriebus divergentibus alongside the divergent geometric series 1 + 2 + 4 + 8 + ⋯. Euler hints that series of this type have finite, negative sums, and he explains what this means for geometric series, but he does not return to discuss 1 + 2 + 3 + 4 + ⋯. In the same publication, Euler writes that the sum of 1 + 1 + 1 + 1 + ⋯ is infinite.^[25]

In popular media

David Leavitt's 2007 novel The Indian Clerk includes a scene where Hardy and Littlewood discuss the meaning of this series. They conclude that Ramanujan has rediscovered ζ(−1), and they take the "lunatic asylum" line in his second letter as a sign that Ramanujan is toying with them.^[26]
Simon McBurney's 2007 play A Disappearing Number focuses on the series in the opening scene. The main character, Ruth, walks into a lecture hall and introduces the idea of a divergent series before proclaiming, "I'm going to show you something really thrilling," namely 1 + 2 + 3 + 4 + ⋯ = − 1/12. As Ruth launches into a derivation of the functional equation of the zeta function, another actor addresses the audience, admitting that they are actors: "But the mathematics is real. It's terrifying, but it's real."^[27][28]
In January 2014, Numberphile produced a YouTube video on the series, which gathered over 1.5 million views in its first month.^[29] The 8-minute video is narrated by Tony Padilla, a physicist at the University of Nottingham. Padilla begins with 1 − 1 + 1 − 1 + ⋯ and 1 − 2 + 3 − 4 + ⋯ and relates the latter to 1 + 2 + 3 + 4 + ⋯ using a term-by-term subtraction similar to Ramanujan's argument.^[30] Numberphile also released a 21-minute version of the video featuring Nottingham physicist Ed Copeland, who describes in more detail how 1 − 2 + 3 − 4 + ⋯ = 1/4 as an Abel sum and 1 + 2 + 3 + 4 + ⋯ = − 1/12 as ζ(−1).^[31] After receiving complaints about the lack of rigour in the first video, Padilla also wrote an explanation on his webpage relating the manipulations in the video to identities between the analytic continuations of the relevant Dirichlet series.^[32]
In the New York Times coverage of the Numberphile video, mathematician Edward Frenkel commented, "This calculation is one of the best-kept secrets in math. No one on the outside knows about it."^[29]
Coverage of this topic in Smithsonian magazine describes the Numberphile video as misleading, and notes that the interpretation of the sum as − 1/12 relies on a specialized meaning for the equals sign, from the techniques of analytic continuation, in which equals means is associated with.^[33]

 *Courtesy of Wikipedia, the free encyclopedia continued . . . .

Johann Carl Friedrich Gauss  

(/ɡaʊs/; German: Gauß [ɡaʊs] ( listen);  

Latin: Carolus Fridericus Gauss; 

30 April 1777 – 23 February 1855) 

 https://en.wikipedia.org/wiki/Carl_Friedrich_Gauss:  There are many other anecdotes about his precocity while a toddler, and he made his first ground-breaking mathematical discoveries while still a teenager. He completed his magnum opus, Disquisitiones Arithmeticae, in 1798, at the age of 21—though it was not published until 1801. This work was fundamental in consolidating number theory as a discipline and has shaped the field to the present day.
Gauss's intellectual abilities attracted the attention of the Duke of Brunswick,^[6][2] who sent him to the Collegium Carolinum (now Braunschweig University of Technology),^[6] which he attended from 1792 to 1795,^[9] and to the University of Göttingen from 1795 to 1798.^[10] While at university, Gauss independently rediscovered several important theorems.^[11] His breakthrough occurred in 1796 when he showed that a regular polygon can be constructed by compass and straightedge if the number of its sides is the product of distinct Fermat primes and a power of 2.^[12] This was a major discovery in an important field of mathematics; construction problems had occupied mathematicians since the days of the Ancient Greeks, and the discovery ultimately led Gauss to choose mathematics instead of philology as a career. Gauss was so pleased with this result that he requested that a regular heptadecagon be inscribed on his tombstone. The stonemason declined, stating that the difficult construction would essentially look like a circle.^[13]
The year 1796 was most productive for both Gauss and number theory. He discovered a construction of the heptadecagon on 30 March.^[10][14] He further advanced modular arithmetic, greatly simplifying manipulations in number theory. On 8 April he became the first to prove the quadratic reciprocity law. This remarkably general law allows mathematicians to determine the solvability of any quadratic equation in modular arithmetic. The prime number theorem, conjectured on 31 May, gives a good understanding of how the prime numbers are distributed among the integers.
Gauss also discovered that every positive integer is representable as a sum of at most three triangular numbers on 10 July and then jotted down in his diary the note: "ΕΥΡΗΚΑ! num = Δ + Δ' + Δ". On 1 October he published a result on the number of solutions of polynomials with coefficients in finite fields, which 150 years later led to the Weil conjectures.
In 1801, Gauss announced that he had calculated the orbit of an asteroid by the name of Ceres.^[10] He also allowed some of his genius to be made public with the publication of Disquisitiones Arithmeticae,^[10] and consequently gained widespread fame.^[10]

Marriage and children

On 9 October 1805,^[15] Gauss married Johanna Osthoff (1780-1809), and had a son and a daughter with her.^[15][16] Johanna died on 11 October 1809,^[15][16][17] and her most recent child, Louis, died the following year.^[15] He then married Minna Waldeck (1788-1831)^[15][16] on 4 August 1810,^[15] and had three more children.^[16] Gauss was never quite the same without his first wife, so he grew to dominate his children, just like his father.^[16] Minna Waldeck died on 12 September 1831.^[15][16]

Later years and death

Gauss on his deathbed (1855)

Gauss's gravesite at Albani Cemetery in Göttingen, Germany

In 1831, Gauss developed a fruitful collaboration with the physics professor Wilhelm Weber, leading to new knowledge in magnetism (including finding a representation for the unit of magnetism in terms of mass, charge, and time) and the discovery of Kirchhoff's circuit laws in electricity.^[18] It was during this time that he formulated his namesake law. They constructed the first electromechanical telegraph in 1833,^[18] which connected the observatory with the institute for physics in Göttingen. Gauss ordered a magnetic observatory to be built in the garden of the observatory, and with Weber founded the "Magnetischer Verein" (magnetic club in German), which supported measurements of Earth's magnetic field in many regions of the world. He developed a method of measuring the horizontal intensity of the magnetic field which was in use well into the second half of the 20th century, and worked out the mathematical theory for separating the inner and outer (magnetospheric) sources of Earth's magnetic field.
Gauss remained mentally active into his old age, even while suffering from gout and general unhappiness.^[18] For example, at the age of 62, he taught himself Russian.^[18]
In 1840, Gauss published his influential Dioptrische Untersuchungen,^[19] in which he gave the first systematic analysis on the formation of images under a paraxial approximation (Gaussian optics).^[20] Among his results, Gauss showed that under a paraxial approximation an optical system can be characterized by its cardinal points^[21] and he derived the Gaussian lens formula.^[22]
In 1845, he became an associated member of the Royal Institute of the Netherlands; when that became the Royal Netherlands Academy of Arts and Sciences in 1851, he joined as a foreign member.^[23]
In 1854, Gauss selected the topic for Bernhard Riemann's Habilitationsvortrag, "Über die Hypothesen, welche der Geometrie zu Grunde liegen" (habilitation lecture About the hypotheses that underlie Geometry).^[24] On the way home from Riemann's lecture, Weber reported that Gauss was full of praise and excitement.^[25]
On 23 February 1855, Gauss died of a heart attack in Göttingen (then Kingdom of Hanover and now Lower Saxony);^[3][18] he is interred in the Albani Cemetery there. Two people gave eulogies at his funeral: Gauss's son-in-law Heinrich Ewald, and Wolfgang Sartorius von Waltershausen, who was Gauss's close friend and biographer. Gauss's brain was preserved and was studied by Rudolf Wagner, who found its mass to be slightly above average, at 1,492 grams, and the cerebral area equal to 219,588 square millimeters^[26] (340.362 square inches). Highly developed convolutions were also found, which in the early 20th century were suggested as the explanation of his genius.^[27]

Religious views

Gauss was a Lutheran Protestant, a member of the St. Albans Evangelical Lutheran church in Göttingen.^[28] Potential evidence that Gauss believed in God comes from his response after solving a problem that had previously defeated him: "Finally, two days ago, I succeeded— not on account of my hard efforts, but by the grace of the Lord."^[29] One of his biographers, G. Waldo Dunnington, described Gauss's religious views as follows:

For him science was the means of exposing the immortal nucleus of the human soul. In the days of his full strength, it furnished him recreation and, by the prospects which it opened up to him, gave consolation. Toward the end of his life, it brought him confidence. Gauss' God was not a cold and distant figment of metaphysics, nor a distorted caricature of embittered theology. To man is not vouchsafed that fullness of knowledge which would warrant his arrogantly holding that his blurred vision is the full light and that there can be none other which might report the truth as does his. For Gauss, not he who mumbles his creed, but he who lives it, is accepted. He believed that a life worthily spent here on earth is the best, the only, preparation for heaven. Religion is not a question of literature, but of life. God's revelation is continuous, not contained in tablets of stone or sacred parchment. A book is inspired when it inspires. The unshakeable idea of personal continuance after death, the firm belief in a last regulator of things, in an eternal, just, omniscient, omnipotent God, formed the basis of his religious life, which harmonized completely with his scientific research.^[30]

Apart from his correspondence, there are not many known details about Gauss' personal creed. Many biographers of Gauss disagree about his religious stance, with Bühler and others considering him a deist with very unorthodox views,^[31][32][33] while Dunnington (though admitting that Gauss did not believe literally in all Christian dogmas and that it is unknown what he believed on most doctrinal and confessional questions) points out that he was, at least, a nominal Lutheran.^[34]
In connection to this, there is a record of a conversation between Rudolf Wagner and Gauss, in which they discussed William Whewell's book Of the Plurality of Worlds. In this work, Whewell had discarded the possibility of existing life in other planets, on the basis of theological arguments, but this was a position with which both Wagner and Gauss disagreed. Later Wagner explained that he did not fully believe in the Bible, though he confessed that he "envied" those who were able to easily believe.^[31][35] This later led them to discuss the topic of faith, and in some other religious remarks, Gauss said that he had been more influenced by theologians like Lutheran minister Paul Gerhardt than by Moses.^[36] Other religious influences included Wilhelm Braubach, Johann Peter Süssmilch, and the New Testament.^[37]
Dunnington further elaborates on Gauss's religious views by writing:

Gauss' religious consciousness was based on an insatiable thirst for truth and a deep feeling of justice extending to intellectual as well as material goods. He conceived spiritual life in the whole universe as a great system of law penetrated by eternal truth, and from this source he gained the firm confidence that death does not end all.^[38]

Gauss declared he firmly believed in the afterlife, and saw spirituality as something essentially important for human beings.^[39] He was quoted stating: "The world would be nonsense, the whole creation an absurdity without immortality,"^[40] and for this statement he was severely criticized by the atheist Eugen Dühring who judged him as a narrow superstitious man.^[41]
Though he was not a church-goer,^[42] Gauss strongly upheld religious tolerance, believing "that one is not justified in disturbing another's religious belief, in which they find consolation for earthly sorrows in time of trouble."^[2] When his son Eugene announced that he wanted to become a Christian missionary, Gauss approved of this, saying that regardless of the problems within religious organizations, missionary work was "a highly honorable" task.^[43]

Family

Gauss's daughter Therese (1816–1864)

Gauss's personal life was overshadowed by the early death of his first wife, Johanna Osthoff, in 1809, soon followed by the death of one child, Louis. Gauss plunged into a depression from which he never fully recovered. He married again, to Johanna's best friend, Friederica Wilhelmine Waldeck, commonly known as Minna. When his second wife died in 1831 after a long illness,^[44] one of his daughters, Therese, took over the household and cared for Gauss for the rest of his life. His mother lived in his house from 1817 until her death in 1839.^[2]
Gauss had six children. With Johanna (1780–1809), his children were Joseph (1806–1873), Wilhelmina (1808–1846) and Louis (1809–1810). With Minna Waldeck he also had three children: Eugene (1811–1896), Wilhelm (1813–1879) and Therese (1816–1864). Eugene shared a good measure of Gauss's talent in languages and computation.^[45] Therese kept house for Gauss until his death, after which she married.
Gauss eventually had conflicts with his sons. He did not want any of his sons to enter mathematics or science for "fear of lowering the family name", as he believed none of them would surpass his own achievements.^[45] Gauss wanted Eugene to become a lawyer, but Eugene wanted to study languages. They had an argument over a party Eugene held, which Gauss refused to pay for. The son left in anger and, in about 1832, emigrated to the United States, where he was quite successful. While working for the American Fur Company in the Midwest, he learned the Sioux language. Later, he moved to Missouri and became a successful businessman. Wilhelm also moved to America in 1837 and settled in Missouri, starting as a farmer and later becoming wealthy in the shoe business in St. Louis. It took many years for Eugene's success to counteract his reputation among Gauss's friends and colleagues. See also the letter from Robert Gauss to Felix Klein on 3 September 1912.

Personality

Carl Gauss was an ardent perfectionist and a hard worker. He was never a prolific writer, refusing to publish work which he did not consider complete and above criticism. This was in keeping with his personal motto pauca sed matura ("few, but ripe"). His personal diaries indicate that he had made several important mathematical discoveries years or decades before his contemporaries published them. Scottish-American mathematician and writer Eric Temple Bell said that if Gauss had published all of his discoveries in a timely manner, he would have advanced mathematics by fifty years.^[46]
Though he did take in a few students, Gauss was known to dislike teaching. It is said that he attended only a single scientific conference, which was in Berlin in 1828. However, several of his students became influential mathematicians, among them Richard Dedekind and Bernhard Riemann.
On Gauss's recommendation, Friedrich Bessel was awarded an honorary doctor degree from Göttingen in March 1811.^[47] Around that time, the two men engaged in an epistolary correspondence.^[48] However, when they met in person in 1825, they quarrelled; the details are unknown.^[49]
Before she died, Sophie Germain was recommended by Gauss to receive her honorary degree; she never received it.^[50]
Gauss usually declined to present the intuition behind his often very elegant proofs—he preferred them to appear "out of thin air" and erased all traces of how he discovered them.^{[citation needed]} This is justified, if unsatisfactorily, by Gauss in his Disquisitiones Arithmeticae, where he states that all analysis (i.e., the paths one traveled to reach the solution of a problem) must be suppressed for sake of brevity.
Gauss supported the monarchy and opposed Napoleon, whom he saw as an outgrowth of revolution.
Gauss summarized his views on the pursuit of knowledge in a letter to Farkas Bolyai dated 2 September 1808 as follows:

It is not knowledge, but the act of learning, not possession but the act of getting there, which grants the greatest enjoyment. When I have clarified and exhausted a subject, then I turn away from it, in order to go into darkness again. The never-satisfied man is so strange; if he has completed a structure, then it is not in order to dwell in it peacefully, but in order to begin another. I imagine the world conqueror must feel thus, who, after one kingdom is scarcely conquered, stretches out his arms for others.^[51]

Careers and achievements

This section needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. (July 2012) (Learn how and when to remove this template message)

Algebra

Title page of Gauss's magnum opus, Disquisitiones Arithmeticae

In his 1799 doctorate in absentia, A new proof of the theorem that every integral rational algebraic function of one variable can be resolved into real factors of the first or second degree, Gauss proved the fundamental theorem of algebra which states that every non-constant single-variable polynomial with complex coefficients has at least one complex root. Mathematicians including Jean le Rond d'Alembert had produced false proofs before him, and Gauss's dissertation contains a critique of d'Alembert's work. Ironically, by today's standard, Gauss's own attempt is not acceptable, owing to the implicit use of the Jordan curve theorem. However, he subsequently produced three other proofs, the last one in 1849 being generally rigorous. His attempts clarified the concept of complex numbers considerably along the way.
Gauss also made important contributions to number theory with his 1801 book Disquisitiones Arithmeticae (Latin, Arithmetical Investigations), which, among other things, introduced the symbol ≡ for congruence and used it in a clean presentation of modular arithmetic, contained the first two proofs of the law of quadratic reciprocity, developed the theories of binary and ternary quadratic forms, stated the class number problem for them, and showed that a regular heptadecagon (17-sided polygon) can be constructed with straightedge and compass.

Astronomy

Portrait of Gauss published in Astronomische Nachrichten (1828)

In the same year, Italian astronomer Giuseppe Piazzi discovered the dwarf planet Ceres. Piazzi could only track Ceres for somewhat more than a month, following it for three degrees across the night sky. Then it disappeared temporarily behind the glare of the Sun. Several months later, when Ceres should have reappeared, Piazzi could not locate it: the mathematical tools of the time were not able to extrapolate a position from such a scant amount of data—three degrees represent less than 1% of the total orbit.
Gauss, who was 24 at the time, heard about the problem and tackled it. After three months of intense work, he predicted a position for Ceres in December 1801—just about a year after its first sighting—and this turned out to be accurate within a half-degree when it was rediscovered by Franz Xaver von Zach on 31 December at Gotha, and one day later by Heinrich Olbers in Bremen.
Gauss's method involved determining a conic section in space, given one focus (the Sun) and the conic's intersection with three given lines (lines of sight from the Earth, which is itself moving on an ellipse, to the planet) and given the time it takes the planet to traverse the arcs determined by these lines (from which the lengths of the arcs can be calculated by Kepler's Second Law). This problem leads to an equation of the eighth degree, of which one solution, the Earth's orbit, is known. The solution sought is then separated from the remaining six based on physical conditions. In this work, Gauss used comprehensive approximation methods which he created for that purpose.^[52]
One such method was the fast Fourier transform. While this method is traditionally attributed to a 1965 paper by J. W. Cooley and J. W. Tukey, Gauss developed it as a trigonometric interpolation method. His paper, Theoria Interpolationis Methodo Nova Tractata,^[53] was only published posthumously in Volume 3 of his collected works. This paper predates the first presentation by Joseph Fourier on the subject in 1807.^[54]
Zach noted that "without the intelligent work and calculations of Doctor Gauss we might not have found Ceres again". Though Gauss had up to that point been financially supported by his stipend from the Duke, he doubted the security of this arrangement, and also did not believe pure mathematics to be important enough to deserve support. Thus he sought a position in astronomy, and in 1807 was appointed Professor of Astronomy and Director of the astronomical observatory in Göttingen, a post he held for the remainder of his life.

Four Gaussian distributions

The discovery of Ceres led Gauss to his work on a theory of the motion of planetoids disturbed by large planets, eventually published in 1809 as Theoria motus corporum coelestium in sectionibus conicis solem ambientum (Theory of motion of the celestial bodies moving in conic sections around the Sun). In the process, he so streamlined the cumbersome mathematics of 18th-century orbital prediction that his work remains a cornerstone of astronomical computation.^{[citation needed]} It introduced the Gaussian gravitational constant, and contained an influential treatment of the method of least squares, a procedure used in all sciences to this day to minimize the impact of measurement error.
Gauss proved the method under the assumption of normally distributed errors (see Gauss–Markov theorem; see also Gaussian). The method had been described earlier by Adrien-Marie Legendre in 1805, but Gauss claimed that he had been using it since 1794 or 1795.^[55] In the history of statistics, this disagreement is called the "priority dispute over the discovery of the method of least squares."^[56]

Geodetic survey

Geodetic survey stone in Garlste (now Garlstedt)

In 1818 Gauss, putting his calculation skills to practical use, carried out a geodetic survey of the Kingdom of Hanover, linking up with previous Danish surveys. To aid the survey, Gauss invented the heliotrope, an instrument that uses a mirror to reflect sunlight over great distances, to measure positions.

Non-Euclidean geometries

Gauss also claimed to have discovered the possibility of non-Euclidean geometries but never published it. This discovery was a major paradigm shift in mathematics, as it freed mathematicians from the mistaken belief that Euclid's axioms were the only way to make geometry consistent and non-contradictory.
Research on these geometries led to, among other things, Einstein's theory of general relativity, which describes the universe as non-Euclidean. His friend Farkas Wolfgang Bolyai with whom Gauss had sworn "brotherhood and the banner of truth" as a student, had tried in vain for many years to prove the parallel postulate from Euclid's other axioms of geometry.
Bolyai's son, János Bolyai, discovered non-Euclidean geometry in 1829; his work was published in 1832. After seeing it, Gauss wrote to Farkas Bolyai: "To praise it would amount to praising myself. For the entire content of the work ... coincides almost exactly with my own meditations which have occupied my mind for the past thirty or thirty-five years."
This unproved statement put a strain on his relationship with Bolyai who thought that Gauss was "stealing" his idea.^[57]
Letters from Gauss years before 1829 reveal him obscurely discussing the problem of parallel lines. Waldo Dunnington, a biographer of Gauss, argues in Gauss, Titan of Science that Gauss was in fact in full possession of non-Euclidean geometry long before it was published by Bolyai, but that he refused to publish any of it because of his fear of controversy.^[58][59]

Theorema Egregium

The geodetic survey of Hanover, which required Gauss to spend summers traveling on horseback for a decade,^[60] fueled Gauss's interest in differential geometry and topology, fields of mathematics dealing with curves and surfaces. Among other things, he came up with the notion of Gaussian curvature. This led in 1828 to an important theorem, the Theorema Egregium (remarkable theorem), establishing an important property of the notion of curvature. Informally, the theorem says that the curvature of a surface can be determined entirely by measuring angles and distances on the surface.
That is, curvature does not depend on how the surface might be embedded in 3-dimensional space or 2-dimensional space.
In 1821, he was made a foreign member of the Royal Swedish Academy of Sciences. Gauss was elected a Foreign Honorary Member of the American Academy of Arts and Sciences in 1822.^[61]

Appraisal of Gauss

The British mathematician Henry John Stephen Smith (1826–1883) gave the following appraisal of Gauss:

If we except the great name of Newton it is probable that no mathematicians of any age or country have ever surpassed Gauss in the combination of an abundant fertility of invention with an absolute rigorousness in demonstration, which the ancient Greeks themselves might have envied. It may seem paradoxical, but it is probably nevertheless true that it is precisely the efforts after logical perfection of form which has rendered the writings of Gauss open to the charge of obscurity and unnecessary difficulty. Gauss says more than once that, for brevity, he gives only the synthesis, and suppresses the analysis of his propositions. If, on the other hand, we turn to a memoir of Euler's, there is a sort of free and luxuriant gracefulness about the whole performance, which tells of the quiet pleasure which Euler must have taken in each step of his work. It is not the least of Gauss' claims to the admiration of mathematicians, that, while fully penetrated with a sense of the vastness of the science, he exacted the utmost rigorousness in every part of it, never passed over a difficulty, as if it did not exist, and never accepted a theorem as true beyond the limits within which it could actually be demonstrated.^[62]

Anecdotes

There are several stories of his early genius. According to one, his gifts became very apparent at the age of three when he corrected, mentally and without fault in his calculations, an error his father had made on paper while calculating finances.
Another story has it that in primary school after the young Gauss misbehaved, his teacher, J.G. Büttner, gave him a task: add a list of integers in arithmetic progression; as the story is most often told, these were the numbers from 1 to 100. The young Gauss reputedly produced the correct answer within seconds, to the astonishment of his teacher and his assistant Martin Bartels.
Gauss's presumed method was to realize that pairwise addition of terms from opposite ends of the list yielded identical intermediate sums: 1 + 100 = 101, 2 + 99 = 101, 3 + 98 = 101, and so on, for a total sum of 50 × 101 = 5050. However, the details of the story are at best uncertain (see^[8] for discussion of the original Wolfgang Sartorius von Waltershausen source and the changes in other versions); some authors, such as Joseph Rotman in his book A first course in Abstract Algebra, question whether it ever happened.
According to Isaac Asimov, Gauss was once interrupted in the middle of a problem and told that his wife was dying. He is purported to have said, "Tell her to wait a moment till I'm done."^[63] This anecdote is briefly discussed in G. Waldo Dunnington's Gauss, Titan of Science where it is suggested that it is an apocryphal story.
He referred to mathematics as "the queen of sciences"^[64] and supposedly once espoused a belief in the necessity of immediately understanding Euler's identity as a benchmark pursuant to becoming a first-class mathematician.^[65]

Commemorations

German 10-Deutsche Mark Banknote (1993; discontinued) featuring Gauss

Gauss (aged about 26, and accompanied by drawings of a heptadecagon, and compass and straightedge) on an East German stamp produced in 1977

From 1989 through 2001, Gauss's portrait, a normal distribution curve and some prominent Göttingen buildings were featured on the German ten-mark banknote. The reverse featured the approach for Hanover. Germany has also issued three postage stamps honoring Gauss. One (no. 725) appeared in 1955 on the hundredth anniversary of his death; two others, nos. 1246 and 1811, in 1977, the 200th anniversary of his birth.
Daniel Kehlmann's 2005 novel Die Vermessung der Welt, translated into English as Measuring the World (2006), explores Gauss's life and work through a lens of historical fiction, contrasting them with those of the German explorer Alexander von Humboldt. A film version directed by Detlev Buck was released in 2012.^[66]
In 2007 a bust of Gauss was placed in the Walhalla temple.^[67]
Things named in honor of Gauss include:

• The Normal Distribution, Gaussian statistics (the bell curve)
• Gauss's Theorem, The Divergence Theorem
• The Gauss Prize, one of the highest honors in mathematics
• Gauss's Law and Gauss's law for magnetism, two of Maxwell's four equations.
• Degaussing, the process of eliminating a magnetic field
• The CGS unit for magnetic field was named gauss in his honour
• The crater Gauss on the Moon^[68]
• Asteroid 1001 Gaussia
• The ship Gauss, used in the Gauss expedition to the Antarctic
• Gaussberg, an extinct volcano discovered by the above-mentioned expedition
• Gauss Tower, an observation tower in Dransfeld, Germany
• In Canadian junior high schools, an annual national mathematics competition (Gauss Mathematics Competition) administered by the Centre for Education in Mathematics and Computing is named in honour of Gauss
• In University of California, Santa Cruz, in Crown College, a dormitory building is named after him
• The Gauss Haus, an NMR center at the University of Utah
• The Carl-Friedrich-Gauß School for Mathematics, Computer Science, Business Administration, Economics, and Social Sciences of Braunschweig University of Technology
• The Gauss Building at the University of Idaho (College of Engineering)
• The Carl-Friedrich-Gauss Gymnasium (a school for grades 5–13) in Worms, Germany
• The 'Gauss House', a common room in the University of Sussex Mathematical and Physical Sciences department.

In 1929 the Polish mathematician Marian Rejewski, who helped to solve the German Enigma cipher machine in December 1932, began studying actuarial statistics at Göttingen. At the request of his Poznań University professor, Zdzisław Krygowski, on arriving at Göttingen Rejewski laid flowers on Gauss's grave.^[69]

Writings

• 1799: Doctoral dissertation on the fundamental theorem of algebra, with the title: Demonstratio nova theorematis omnem functionem algebraicam rationalem integram unius variabilis in factores reales primi vel secundi gradus resolvi posse ("New proof of the theorem that every integral algebraic function of one variable can be resolved into real factors (i.e., polynomials) of the first or second degree")
• 1801: Disquisitiones Arithmeticae (Latin). A German translation by H. Maser "Untersuchungen über höhere Arithmetik (Disquisitiones Arithmeticae & other papers on number theory) (Second edition)". New York: Chelsea F.C. 1965. ISBN 0-8284-0191-8., pp. 1–453. English translation by Arthur A. Clarke "Disquisitiones Arithmeticae (Second, corrected edition)". New York: Springer. 1986. ISBN 0-387-96254-9..
• 1808: "Theorematis arithmetici demonstratio nova". Göttingen: Commentationes Societatis Regiae Scientiarum Gottingensis. 16.. German translation by H. Maser "Untersuchungen über höhere Arithmetik (Disquisitiones Arithmeticae & other papers on number theory) (Second edition)". New York: Chelsea F.C. 1965. ISBN 0-8284-0191-8., pp. 457–462 [Introduces Gauss's lemma, uses it in the third proof of quadratic reciprocity]
• 1809: Theoria Motus Corporum Coelestium in sectionibus conicis solem ambientium (Theorie der Bewegung der Himmelskörper, die die Sonne in Kegelschnitten umkreisen), Theory of the Motion of Heavenly Bodies Moving about the Sun in Conic Sections (English translation by C. H. Davis), reprinted 1963, Dover, New York.
• 1811: "Summatio serierun quarundam singularium". Göttingen: Commentationes Societatis Regiae Scientiarum Gottingensis.. German translation by H. Maser "Untersuchungen über höhere Arithmetik (Disquisitiones Arithmeticae & other papers on number theory) (Second edition)". New York: Chelsea F.C. 1965. ISBN 0-8284-0191-8., pp. 463–495 [Determination of the sign of the quadratic Gauss sum, uses this to give the fourth proof of quadratic reciprocity]
• 1812: Disquisitiones Generales Circa Seriem Infinitam ${\displaystyle 1+{\frac {\alpha \beta }{\gamma .1}}+{\mbox{etc.}}}$
• 1818: "Theorematis fundamentallis in doctrina de residuis quadraticis demonstrationes et amplicationes novae". Göttingen: Commentationes Societatis Regiae Scientiarum Gottingensis.. German translation by H. Maser "Untersuchungen über höhere Arithmetik (Disquisitiones Arithmeticae & other papers on number theory) (Second edition)". New York: Chelsea F.C. 1965. ISBN 0-8284-0191-8., pp. 496–510 [Fifth and sixth proofs of quadratic reciprocity]
• 1821, 1823 and 1826: Theoria combinationis observationum erroribus minimis obnoxiae. Drei Abhandlungen betreffend die Wahrscheinlichkeitsrechnung als Grundlage des Gauß'schen Fehlerfortpflanzungsgesetzes. (Three essays concerning the calculation of probabilities as the basis of the Gaussian law of error propagation) English translation by G. W. Stewart, 1987, Society for Industrial Mathematics.
• 1827: Disquisitiones generales circa superficies curvas, Commentationes Societatis Regiae Scientiarum Gottingesis Recentiores. Volume VI, pp. 99–146. "General Investigations of Curved Surfaces" (published 1965) Raven Press, New York, translated by J.C.Morehead and A.M.Hiltebeitel
• 1828: "Theoria residuorum biquadraticorum, Commentatio prima". Göttingen: Commentationes Societatis Regiae Scientiarum Gottingensis. 6.. German translation by H. Maser "Untersuchungen über höhere Arithmetik (Disquisitiones Arithmeticae & other papers on number theory) (Second edition)". New York: Chelsea F.C. 1965. ISBN 0-8284-0191-8., pp. 511–533 [Elementary facts about biquadratic residues, proves one of the supplements of the law of biquadratic reciprocity (the biquadratic character of 2)]
• 1832: "Theoria residuorum biquadraticorum, Commentatio secunda". Göttingen: Commentationes Societatis Regiae Scientiarum Gottingensis. 7.. German translation by H. Maser "Untersuchungen über höhere Arithmetik (Disquisitiones Arithmeticae & other papers on number theory) (Second edition)". New York: Chelsea F.C. 1965. ISBN 0-8284-0191-8., pp. 534–586 [Introduces the Gaussian integers, states (without proof) the law of biquadratic reciprocity, proves the supplementary law for 1 + i]
• "Intensitas vis magneticae terrestris ad mensuram absolutam revocata". Commentationes Societatis Regiae Scientiarum Gottingensis Recentiores. 8: 3–44. 1832. English translation
• 1843/44: Untersuchungen über Gegenstände der Höheren Geodäsie. Erste Abhandlung, Abhandlungen der Königlichen Gesellschaft der Wissenschaften in Göttingen. Zweiter Band, pp. 3–46
• 1846/47: Untersuchungen über Gegenstände der Höheren Geodäsie. Zweite Abhandlung, Abhandlungen der Königlichen Gesellschaft der Wissenschaften in Göttingen. Dritter Band, pp. 3–44
• Mathematisches Tagebuch 1796–1814, Ostwaldts Klassiker, Verlag Harri Deutsch 2005, mit Anmerkungen von Neumamn, ISBN 978-3-8171-3402-1 (English translation with annotations by Jeremy Gray: Expositiones Math. 1984)

Gauss's collective works are online at dz-srv1.sub.uni-goettingen.de Uni-goettingen.de includes German translations of Latin texts and commentaries by various authorities.

See also

• Carl Friedrich Gauss Prize
• Gaussian elimination
• German inventors and discoverers
• List of things named after Carl Friedrich Gauss
• Romanticism in science