An Australian slide rule used for machine gun fire calculations.
Successful calculation of an artillery trajectory requires the consideration of meteorological factors and ballistics information. This rule is important, as it simplifies this process, eliminating the traditional use of protractors, logarithmic tables, map scales, trigonometric tables, etc. Notable features are the provision of wind gauge and spirit thermometer.
Used for medium machine-gun laying of indirect fire. It was designed for the Vickers gun or any other type on a fixed mounting or tripod. Provision is made for ranges up to 3000 yards with mark VII ammunition. All calculations are made by moving the graduated slide to appropriate positions against corresponding graduations on the fixed portion.
This is an improved and simplified model of the earlier Gunner's Calculator.
World Coins Mystery Box Coolstax Vault
This is a sample: Unique Coin Slides:
These one-of-a-kind coin slides are refurbished preowned parts, unless designated new old stock.
Each is completely disassembled, cleaned, lubricated and tested to make sure that it works smoothly.
If the quality is unacceptable, it can be returned for a full refund.
All are available in a quantity of one unless noted.
Cantore Arithmetic is able to state word trying.
1. Crazy Horse doctor and Dr. Ziegler.
Cantore Arithmetic is not interested in NASA. The words applicable are word accurate and your journey so[thus] fare[long] has been word equated word theft. This word Common denominator equated words[worth] long pause[Pause.].
1. Now in Sacramento I had a experience that drove home the word paranoid as at Dorchester with words address 815 bowel boa the worth to words is whoa.
2. My mother had a nervous breakdown and had to Europe while E.Kp junior had a divorce, the paranoia equated word doctors.
The fact that word Diagnosis is word select[Safeway] is word simply complex. Now, the fact that computers are not available and a laptop is a word dance studio the Doctor in Sacramento needed[Boudin] as 22 22nd Avenue is word gone, the Farm is word gone, the word security is word gone and this is not what word they had equated with word applied. So, now that it seems that Cantore Arithmetic is not needed the deeper this goes[Dr. Byron Kilgore] the more that that Doctor needs to be accommodated[Dr. Luis Vuksinick, MD].
Word virtue[Virtue] is a keyboard that is made to direct in other words I am on the computer and my fingers are typing and keys are antibiotic so that word worry does not inhabit word antibiotic but rather embraces the crutch. The entire keyboard is set to word design in word Probability as you are not meant to loose hope:
You searched for
"VIRTUE" in the KJV Bible
6 Instances - Page 1 of 1 - Sort by Book Order - Feedback
- 2 Peter 1:5chapter context similar meaning copy save
- And beside this, giving all diligence, add to your faith virtue; and to virtueknowledge;
- Luke 8:46chapter context similar meaning copy save
- And Jesus said, Somebody hath touched me: for I perceive that virtue is gone out of me.
- Luke 6:19chapter context similar meaning copy save
- And the whole multitude sought to touch him: for there went virtue out of him, and healed them all.
- Mark 5:30chapter context similar meaning copy save
- And Jesus, immediately knowing in himself that virtue had gone out of him, turned him about in the press, and said, Who touched my clothes?
- 2 Peter 1:3chapter context similar meaning copy save
- According as his divine power hath given unto us all things that pertain unto life and godliness, through the knowledge of him that hath called us to glory and virtue:
- Philippians 4:8chapter context similar meaning copy save
- Finally, brethren, whatsoever things are true, whatsoever things are honest, whatsoever things are just, whatsoever things are pure, whatsoever things are lovely, whatsoever things are of good report; if there be any virtue, and if there be any praise, think on these things.
1. Word Here goes;
Venn diagram
From Wikipedia, the free encyclopedia
Example[edit]

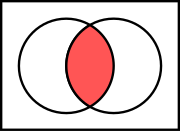
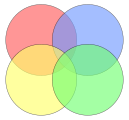
Sets A (creatures with two legs) and B (creatures that can fly) This example involves two sets, A and B, represented here as coloured circles. The yellow circle, set A, represents all living creatures that are two-legged. The blue circle, set B, represents the living creatures that can fly. Each separate type of creature can be imagined as a point somewhere in the diagram. Living creatures that both can fly and have two legs—for example, parrots—are then in both sets, so they correspond to points in the area where the blue and orange circles overlap. That area contains all such and only such living creatures. Humans and penguins are bipedal, and so are then in the orange circle, but since they cannot fly they appear in the left part of the orange circle, where it does not overlap with the blue circle. Mosquitoes have six legs, and fly, so the point for mosquitoes is in the part of the blue circle that does not overlap with the orange one. Creatures that are not two-legged and cannot fly (for example, whales and spiders) would all be represented by points outside both circles.
The combined area of sets A and B is called the union of A and B, denoted by A ∪ B. The union in this case contains all living creatures that are either two-legged or that can fly (or both). The area in both A and B, where the two sets overlap, is called the intersection of A and B, denoted by A ∩ B. For example, the intersection of the two sets is not empty, because there are points that represent creatures that are in both the orange and blue circles. History[edit]
Venn diagrams were introduced in 1880 by John Venn in a paper entitled On the Diagrammatic and Mechanical Representation of Propositions and Reasonings in the "Philosophical Magazine and Journal of Science", about the different ways to represent propositions by diagrams.[1][2] The use of these types of diagrams in formal logic, according to Ruskey and M. Weston, is "not an easy history to trace, but it is certain that the diagrams that are popularly associated with Venn, in fact, originated much earlier. They are rightly associated with Venn, however, because he comprehensively surveyed and formalized their usage, and was the first to generalize them".[3] Venn himself did not use the term "Venn diagram" and referred to his invention as "Eulerian Circles".[2] For example, in the opening sentence of his 1880 article Venn writes, "Schemes of diagrammatic representation have been so familiarly introduced into logical treatises during the last century or so, that many readers, even those who have made no professional study of logic, may be supposed to be acquainted with the general nature and object of such devices. Of these schemes one only, viz. that commonly called 'Eulerian circles,' has met with any general acceptance..."[1] The first to use the term "Venn diagram" was Clarence Irving Lewis in 1918, in his book "A Survey of Symbolic Logic".[3] Venn diagrams are very similar to Euler diagrams, which were invented by Leonhard Euler in the 18th century.[note 1] M. E. Baron has noted that Leibniz (1646–1716) in the 17th century produced similar diagrams before Euler, but much of it was unpublished. She also observes even earlier Euler-like diagrams by Ramon Lull in the 13th Century.[4] In the 20th century, Venn diagrams were further developed. D.W. Henderson showed in 1963 that the existence of an n-Venn diagram with n-fold rotational symmetry implied thatn was a prime number.[5] He also showed that such symmetric Venn diagrams exist when n is 5 or 7. In 2002 Peter Hamburger found symmetric Venn diagrams for n = 11 and in 2003, Griggs, Killian, and Savage showed that symmetric Venn diagrams exist for all other primes. Thus rotationally symmetric Venn diagrams exist if and only if n is a prime number.[6] Venn diagrams and Euler diagrams were incorporated as part of instruction in set theory as part of the new math movement in the 1960s. Since then, they have also been adopted in the curriculum of other fields such as reading.[7] Overview[edit]
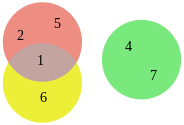
A Venn diagram is constructed with a collection of simple closed curves drawn in a plane. According to Lewis,[8] the "principle of these diagrams is that classes [or sets] be represented by regions in such relation to one another that all the possible logical relations of these classes can be indicated in the same diagram. That is, the diagram initially leaves room for any possible relation of the classes, and the actual or given relation, can then be specified by indicating that some particular region is null or is not-null".[8]:157 Venn diagrams normally comprise overlapping circles. The interior of the circle symbolically represents the elements of the set, while the exterior represents elements that are not members of the set. For instance, in a two-set Venn diagram, one circle may represent the group of all wooden objects, while another circle may represent the set of all tables. The overlapping area or intersection would then represent the set of all wooden tables. Shapes other than circles can be employed as shown below by Venn's own higher set diagrams. Venn diagrams do not generally contain information on the relative or absolute sizes (cardinality) of sets; i.e. they are schematic diagrams. Venn diagrams are similar to Euler diagrams. However, a Venn diagram for n component sets must contain all 2n hypothetically possible zones that correspond to some combination of inclusion or exclusion in each of the component sets. Euler diagrams contain only the actually possible zones in a given context. In Venn diagrams, a shaded zone may represent an empty zone, whereas in an Euler diagram the corresponding zone is missing from the diagram. For example, if one set represents dairy products and anothercheeses, the Venn diagram contains a zone for cheeses that are not dairy products. Assuming that in the context cheese means some type of dairy product, the Euler diagram has the cheese zone entirely contained within the dairy-product zone—there is no zone for (non-existent) non-dairy cheese. This means that as the number of contours increases, Euler diagrams are typically less visually complex than the equivalent Venn diagram, particularly if the number of non-empty intersections is small.[9] The difference between Euler and Venn diagrams can be seen in the following example. Take the three sets:
The Venn and the Euler diagram of those sets are:
Extensions to higher numbers of sets[edit]
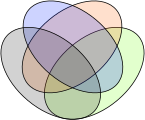
Venn diagrams typically represent two or three sets, but there are forms that allow for higher numbers. Shown below, four intersecting spheres form the highest order Venn diagram that has the symmetry of a simplex and can be visually represented. The 16 intersections correspond to the vertices of a tesseract (or the cells of a 16-cell respectively). For higher numbers of sets, some loss of symmetry in the diagrams is unavoidable. Venn was keen to find "symmetrical figures...elegant in themselves,"[10] that represented higher numbers of sets, and he devised a four-set diagram using ellipses (see below). He also gave a construction for Venn diagrams for any number of sets, where each successive curve that delimits a set interleaves with previous curves, starting with the three-circle diagram. Venn's construction for 4 sets
Venn's construction for 5 sets
Venn's construction for 6 sets
Venn's four-set diagram using ellipses
Non-example: This
Euler diagram is
not a Venn diagram for four sets as it has only 13 regions (excluding the outside); there is no region where only the yellow and blue, or only the red and green circles meet.
Five-set Venn diagram using congruent ellipses in a 5-fold
rotationally symmetrical arrangement devised by
Branko Grünbaum. Labels have been simplified for greater readability; for example,
A denotes
A ∩
Bc ∩
Cc ∩
Dc∩
Ec, while
BCE denotes
Ac ∩
B ∩
C∩
Dc ∩
E.
Edwards' Venn diagrams[edit]
A. W. F. Edwards constructed a series of Venn diagrams for higher numbers of sets by segmenting the surface of a sphere. For example, three sets can be easily represented by taking three hemispheres of the sphere at right angles (x = 0, y = 0 and z = 0). A fourth set can be added to the representation by taking a curve similar to the seam on a tennis ball, which winds up and down around the equator, and so on. The resulting sets can then be projected back to a plane to give cogwheel diagrams with increasing numbers of teeth, as shown here. These diagrams were devised while designing a stained-glass window in memory of Venn. Other diagrams[edit]
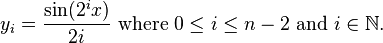
Related concepts[edit]

Venn diagram as a truth table Venn diagrams correspond to truth tables for the propositions 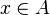 ,
, 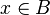 , etc., in the sense that each region of Venn diagram corresponds to one row of the truth table.[12][13] Another way of representing sets is with R-Diagrams.
, etc., in the sense that each region of Venn diagram corresponds to one row of the truth table.[12][13] Another way of representing sets is with R-Diagrams.









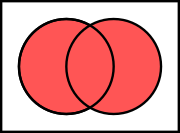

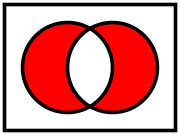

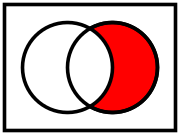

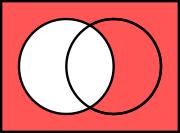


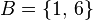












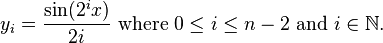

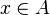 ,
, 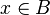 , etc., in the sense that each region of Venn diagram corresponds to one row of the truth table.
, etc., in the sense that each region of Venn diagram corresponds to one row of the truth table.








No comments:
Post a Comment