

Cantore Arithmetic has circulatory equating system to arrange the idea that cancer is to made in the numeric order of the King James Version to discover. The arrangement takes system to the thesaurus as Cantore Arithmetic begins to work in combination to the known at the local doctors offices. The idea is to comb it in to see the lines as in ley lines in order to untangle the cancer at a placebos rate.
To place to picture is to comprehend the human circulatory rate as the skin is always moving as the circulation goes to the Examiner vs. The Chronicle in San Francisco of course. The idea has been ongoing as at 22 22nd Avenue cancer was a big event. The commitment to idea of the good book having the clue is still to format and must be proofed, please consider strongly the Christian Ministries as I am only using the King James Version and there is belief by myself that the actual cure(cue Boudin) is in The Living Bible.
To understand at quote unquote system I will employ word rule and oddly that looks to the calf. This is what a doctor may find as discovery for the information is copious. At that, the blanket of the cover to what is cancer now has a sequence. Now, this all seems to much and the impossible at the work that the doctors have already at their desk to the patient, however the ability to understand Fibonacci and that there is no patent on his work brings to now a bottle.
Bible Verses About Rules
Bible verses related to Rules from the King James Version (KJV) by Relevance
- Sort By Book Order
Bible Verses About Golden Rule
Bible Verses About Golden Rule
Bible verses related to Golden Rule from the King James Version (KJV) by Relevance
Topics and verses are auto-generated from user searches. If a verse or topic does not belong, please contact us. Some scripture references/categories courtesy of Open Bible .info under CC BY 3.0
Related Bible Dictionary Terms:
Golden calf
Fibonacci sequence

In mathematics, the Fibonacci sequence is a sequence in which each number is the sum of the two preceding ones. Numbers that are part of the Fibonacci sequence are known as Fibonacci numbers, commonly denoted Fn . The sequence commonly starts from 0 and 1, although some authors start the sequence from 1 and 1 or sometimes (as did Fibonacci) from 1 and 2. Starting from 0 and 1, the first few values in the sequence are:[1]
- 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144.
The Fibonacci numbers were first described in Indian mathematics,[2][3][4] as early as 200 BC in work by Pingalaon enumerating possible patterns of Sanskrit poetry formed from syllables of two lengths. They are named after the Italian mathematician Leonardo of Pisa, also known as Fibonacci, who introduced the sequence to Western European mathematics in his 1202 book Liber Abaci.[5]
Fibonacci numbers appear unexpectedly often in mathematics, so much so that there is an entire journal dedicated to their study, the Fibonacci Quarterly. Applications of Fibonacci numbers include computer algorithms such as the Fibonacci search techniqueand the Fibonacci heap data structure, and graphs called Fibonacci cubes used for interconnecting parallel and distributed systems. They also appear in biological settings, such as branching in trees, the arrangement of leaves on a stem, the fruit sprouts of a pineapple, the flowering of an artichoke, and the arrangement of a pine cone's bracts, though they don't occur in all species.
Fibonacci numbers are also strongly related to the golden ratio: Binet's formula expresses the nth Fibonacci number in terms of n and the golden ratio, and implies that the ratio of two consecutive Fibonacci numbers tends to the golden ratio as n increases. Fibonacci numbers are also closely related to Lucas numbers, which obey the same recurrence relation and with the Fibonacci numbers form a complementary pair of Lucas sequences.
Definition[edit]

The Fibonacci numbers may be defined by the recurrence relation[6]
Under some older definitions, the value is omitted, so that the sequence starts with and the recurrence is valid for n > 2.[7][8]
The first 20 Fibonacci numbers Fn are:[1]
F0 F1 F2 F3 F4 F5 F6 F7 F8 F9 F10 F11 F12 F13 F14 F15 F16 F17 F18 F19 0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181
History[edit]
India[edit]

The Fibonacci sequence appears in Indian mathematics, in connection with Sanskrit prosody.[3][9][10] In the Sanskrit poetic tradition, there was interest in enumerating all patterns of long (L) syllables of 2 units duration, juxtaposed with short (S) syllables of 1 unit duration. Counting the different patterns of successive L and S with a given total duration results in the Fibonacci numbers: the number of patterns of duration m units is Fm+1.[4]
Knowledge of the Fibonacci sequence was expressed as early as Pingala (c. 450 BC–200 BC). Singh cites Pingala's cryptic formula misrau cha ("the two are mixed") and scholars who interpret it in context as saying that the number of patterns for m beats (Fm+1) is obtained by adding one [S] to the Fm cases and one [L] to the Fm−1cases.[11] Bharata Muni also expresses knowledge of the sequence in the Natya Shastra (c. 100 BC–c. 350 AD).[12][2] However, the clearest exposition of the sequence arises in the work of Virahanka (c. 700 AD), whose own work is lost, but is available in a quotation by Gopala (c. 1135):[10]
Hemachandra (c. 1150) is credited with knowledge of the sequence as well,[2] writing that "the sum of the last and the one before the last is the number ... of the next mātrā-vṛtta."[14][15]
Europe[edit]

the indices from present to XII (months) as Latin ordinals and Roman numerals and the numbers (of rabbit pairs) as Hindu-Arabic numerals starting with 1, 2, 3, 5 and ending with 377.
The Fibonacci sequence first appears in the book Liber Abaci (The Book of Calculation, 1202) by Fibonacci[16][17] where it is used to calculate the growth of rabbit populations.[18][19] Fibonacci considers the growth of an idealized (biologically unrealistic) rabbit population, assuming that: a newly born breeding pair of rabbits are put in a field; each breeding pair mates at the age of one month, and at the end of their second month they always produce another pair of rabbits; and rabbits never die, but continue breeding forever. Fibonacci posed the puzzle: how many pairs will there be in one year?
- At the end of the first month, they mate, but there is still only 1 pair.
- At the end of the second month they produce a new pair, so there are 2 pairs in the field.
- At the end of the third month, the original pair produce a second pair, but the second pair only mate to gestate for a month, so there are 3 pairs in all.
- At the end of the fourth month, the original pair has produced yet another new pair, and the pair born two months ago also produces their first pair, making 5 pairs.
At the end of the nth month, the number of pairs of rabbits is equal to the number of mature pairs (that is, the number of pairs in month n – 2) plus the number of pairs alive last month (month n – 1). The number in the nth month is the nth Fibonacci number.[20]
The name "Fibonacci sequence" was first used by the 19th-century number theorist Édouard Lucas.[21]

Relation to the golden ratio[edit]
Closed-form expression [edit]
Like every sequence defined by a linear recurrence with constant coefficients, the Fibonacci numbers have a closed-form expression. It has become known as Binet's formula, named after French mathematician Jacques Philippe Marie Binet, though it was already known by Abraham de Moivre and Daniel Bernoulli:[22]
where
is the golden ratio, and ψ is its conjugate:[23]
Since , this formula can also be written as
To see the relation between the sequence and these constants,[24] note that φ and ψ are both solutions of the equation and thus so the powers of φ and ψ satisfy the Fibonacci recursion. In other words,
It follows that for any values a and b, the sequence defined by
satisfies the same recurrence,
If a and b are chosen so that U0 = 0 and U1 = 1 then the resulting sequence Un must be the Fibonacci sequence. This is the same as requiring a and bsatisfy the system of equations:
which has solution
producing the required formula.
Taking the starting values U0 and U1 to be arbitrary constants, a more general solution is:
where
Computation by rounding[edit]
Since for all n ≥ 0, the number Fn is the closest integer to . Therefore, it can be found by rounding, using the nearest integer function:
In fact, the rounding error is very small, being less than 0.1 for n ≥ 4, and less than 0.01 for n ≥ 8. This formula is easily inverted to find an index of a Fibonacci number F:
Instead using the floor function gives the largest index of a Fibonacci number that is not greater than F:
Magnitude[edit]
Since Fn is asymptotic to , the number of digits in Fn is asymptotic to . As a consequence, for every integer d > 1 there are either 4 or 5 Fibonacci numbers with d decimal digits.
More generally, in the base b representation, the number of digits in Fn is asymptotic to
Limit of consecutive quotients[edit]
Johannes Kepler observed that the ratio of consecutive Fibonacci numbers converges. He wrote that "as 5 is to 8 so is 8 to 13, practically, and as 8 is to 13, so is 13 to 21 almost", and concluded that these ratios approach the golden ratio [27][28]
This convergence holds regardless of the starting values and , unless . This can be verified using Binet's formula. For example, the initial values 3 and 2 generate the sequence 3, 2, 5, 7, 12, 19, 31, 50, 81, 131, 212, 343, 555, ... . The ratio of consecutive terms in this sequence shows the same convergence towards the golden ratio.
In general, , because the ratios between consecutive Fibonacci numbers approaches .

Successive tilings of the plane and a graph of approximations to the golden ratio calculated by dividing each Fibonacci number by the previous
Decomposition of powers[edit]
Since the golden ratio satisfies the equation
this expression can be used to decompose higher powers as a linear function of lower powers, which in turn can be decomposed all the way down to a linear combination of and 1. The resulting recurrence relationships yield Fibonacci numbers as the linear coefficients:
These expressions are also true for n < 1 if the Fibonacci sequence Fn is extended to negative integers using the Fibonacci rule
Identification[edit]
Binet's formula provides a proof that a positive integer x is a Fibonacci number if and only if at least one of or is a perfect square.[29]This is because Binet's formula, which can be written as , can be multiplied by and solved as a quadratic equationin via the quadratic formula:
Comparing this to , it follows that
In particular, the left-hand side is a perfect square.
Matrix form[edit]
A 2-dimensional system of linear difference equations that describes the Fibonacci sequence is
which yields . The eigenvalues of the matrix A are and corresponding to the respective eigenvectors
Equivalently, the same computation may be performed by diagonalization of A through use of its eigendecomposition:
which again yields
The matrix A has a determinant of −1, and thus it is a 2 × 2 unimodular matrix.
This property can be understood in terms of the continued fraction representation for the golden ratio:
The Fibonacci numbers occur as the ratio of successive convergents of the continued fraction for φ, and the matrix formed from successive convergents of any continued fraction has a determinant of +1 or −1. The matrix representation gives the following closed-form expression for the Fibonacci numbers:
For a given n, this matrix can be computed in O(log(n)) arithmetic operations, using the exponentiation by squaring method.
Taking the determinant of both sides of this equation yields Cassini's identity,
Moreover, since AnAm = An+m for any square matrix A, the following identities can be derived (they are obtained from two different coefficients of the matrix product, and one may easily deduce the second one from the first one by changing n into n + 1),
In particular, with m = n,
These last two identities provide a way to compute Fibonacci numbers recursively in O(log(n)) arithmetic operations and in time O(M(n) log(n)), where M(n) is the time for the multiplication of two numbers of n digits. This matches the time for computing the nth Fibonacci number from the closed-form matrix formula, but with fewer redundant steps if one avoids recomputing an already computed Fibonacci number (recursion with memoization).[30]
Combinatorial identities[edit]
Combinatorial proofs[edit]
Most identities involving Fibonacci numbers can be proved using combinatorial arguments using the fact that can be interpreted as the number of (possibly empty) sequences of 1s and 2s whose sum is . This can be taken as the definition of with the conventions , meaning no such sequence exists whose sum is −1, and , meaning the empty sequence "adds up" to 0. In the following, is the cardinality of a set:
In this manner the recurrence relation
In a similar manner it may be shown that the sum of the first Fibonacci numbers up to the nth is equal to the (n + 2)nd Fibonacci number minus 1.[31] In symbols:
This may be seen by dividing all sequences summing to based on the location of the first 2. Specifically, each set consists of those sequences that start until the last two sets each with cardinality 1.
Following the same logic as before, by summing the cardinality of each set we see that
... where the last two terms have the value . From this it follows that .
A similar argument, grouping the sums by the position of the first 1 rather than the first 2 gives two more identities:
A different trick may be used to prove
Symbolic method[edit]
The sequence is also considered using the symbolic method.[33] More precisely, this sequence corresponds to a specifiable combinatorial class. The specification of this sequence is . Indeed, as stated above, the -th Fibonacci number equals the number of combinatorial compositions (ordered partitions) of using terms 1 and 2.
It follows that the ordinary generating function of the Fibonacci sequence, , is the rational function
Induction proofs[edit]
Fibonacci identities often can be easily proved using mathematical induction.
For example, reconsider
and so we have the formula for
Similarly, add to both sides of
Binet formula proofs[edit]
The Binet formula is
For example, to prove that note that the left hand side multiplied by becomes
Other identities[edit]
Numerous other identities can be derived using various methods. Here are some of them:[34]
Cassini's and Catalan's identities[edit]
Cassini's identity states that
d'Ocagne's identity[edit]
More generally,[34]
or alternatively
Putting k = 2 in this formula, one gets again the formulas of the end of above section Matrix form.
Generating function[edit]
The generating function of the Fibonacci sequence is the power series
This series is convergent for any complex number satisfying and its sum has a simple closed form:[35]
This can be proved by multiplying by :
where all terms involving for cancel out because of the defining Fibonacci recurrence relation.
The partial fraction decomposition is given by
The related function is the generating function for the negafibonacci numbers, and satisfies the functional equation
Using equal to any of 0.01, 0.001, 0.0001, etc. lays out the first Fibonacci numbers in the decimal expansion of . For example,
Reciprocal sums[edit]
Infinite sums over reciprocal Fibonacci numbers can sometimes be evaluated in terms of theta functions. For example, the sum of every odd-indexed reciprocal Fibonacci number can be written as
and the sum of squared reciprocal Fibonacci numbers as
If we add 1 to each Fibonacci number in the first sum, there is also the closed form
and there is a nested sum of squared Fibonacci numbers giving the reciprocal of the golden ratio,
The sum of all even-indexed reciprocal Fibonacci numbers is[36]
So the reciprocal Fibonacci constant is[37]
Moreover, this number has been proved irrational by Richard André-Jeannin.[38]
Millin's series gives the identity[39]
Primes and divisibility[edit]
Divisibility properties[edit]
Every third number of the sequence is even (a multiple of ) and, more generally, every kth number of the sequence is a multiple of Fk. Thus the Fibonacci sequence is an example of a divisibility sequence. In fact, the Fibonacci sequence satisfies the stronger divisibility property[40][41]
In particular, any three consecutive Fibonacci numbers are pairwise coprime because both and . That is,
for every n.
Every prime number p divides a Fibonacci number that can be determined by the value of p modulo 5. If p is congruent to 1 or 4 modulo 5, then p divides Fp−1, and if p is congruent to 2 or 3 modulo 5, then, p divides Fp+1. The remaining case is that p = 5, and in this case p divides Fp.
These cases can be combined into a single, non-piecewise formula, using the Legendre symbol:[42]
Primality testing[edit]
The above formula can be used as a primality test in the sense that if
Fibonacci primes[edit]
A Fibonacci prime is a Fibonacci number that is prime. The first few are:[44]
- 2, 3, 5, 13, 89, 233, 1597, 28657, 514229, ...
Fibonacci primes with thousands of digits have been found, but it is not known whether there are infinitely many.[45]
Fkn is divisible by Fn, so, apart from F4 = 3, any Fibonacci prime must have a prime index. As there are arbitrarily long runs of composite numbers, there are therefore also arbitrarily long runs of composite Fibonacci numbers.
No Fibonacci number greater than F6 = 8 is one greater or one less than a prime number.[46]
The only nontrivial square Fibonacci number is 144.[47] Attila Pethő proved in 2001 that there is only a finite number of perfect power Fibonacci numbers.[48] In 2006, Y. Bugeaud, M. Mignotte, and S. Siksek proved that 8 and 144 are the only such non-trivial perfect powers.[49]
1, 3, 21, and 55 are the only triangular Fibonacci numbers, which was conjectured by Vern Hoggatt and proved by Luo Ming.[50]
No Fibonacci number can be a perfect number.[51] More generally, no Fibonacci number other than 1 can be multiply perfect,[52] and no ratio of two Fibonacci numbers can be perfect.[53]
Prime divisors[edit]
With the exceptions of 1, 8 and 144 (F1 = F2, F6 and F12) every Fibonacci number has a prime factor that is not a factor of any smaller Fibonacci number (Carmichael's theorem).[54] As a result, 8 and 144 (F6 and F12) are the only Fibonacci numbers that are the product of other Fibonacci numbers.[55]
The divisibility of Fibonacci numbers by a prime p is related to the Legendre symbol which is evaluated as follows:
If p is a prime number then
For example,
It is not known whether there exists a prime p such that
Such primes (if there are any) would be called Wall–Sun–Sun primes.
Also, if p ≠ 5 is an odd prime number then:[58]
Example 1. p = 7, in this case p ≡ 3 (mod 4) and we have:
Example 2. p = 11, in this case p ≡ 3 (mod 4) and we have:
Example 3. p = 13, in this case p ≡ 1 (mod 4) and we have:
Example 4. p = 29, in this case p ≡ 1 (mod 4) and we have:
For odd n, all odd prime divisors of Fn are congruent to 1 modulo 4, implying that all odd divisors of Fn (as the products of odd prime divisors) are congruent to 1 modulo 4.[59]
For example,
All known factors of Fibonacci numbers F(i ) for all i < 50000 are collected at the relevant repositories.[60][61]
Periodicity modulo n[edit]
If the members of the Fibonacci sequence are taken mod n, the resulting sequence is periodic with period at most 6n.[62] The lengths of the periods for various n form the so-called Pisano periods.[63] Determining a general formula for the Pisano periods is an open problem, which includes as a subproblem a special instance of the problem of finding the multiplicative order of a modular integer or of an element in a finite field. However, for any particular n, the Pisano period may be found as an instance of cycle detection.
Generalizations[edit]
The Fibonacci sequence is one of the simplest and earliest known sequences defined by a recurrence relation, and specifically by a linear difference equation. All these sequences may be viewed as generalizations of the Fibonacci sequence. In particular, Binet's formula may be generalized to any sequence that is a solution of a homogeneous linear difference equation with constant coefficients.
Some specific examples that are close, in some sense, to the Fibonacci sequence include:
- Generalizing the index to negative integers to produce the negafibonacci numbers.
- Generalizing the index to real numbers using a modification of Binet's formula.[34]
- Starting with other integers. Lucas numbers have L1 = 1, L2 = 3, and Ln = Ln−1 + Ln−2. Primefree sequences use the Fibonacci recursion with other starting points to generate sequences in which all numbers are composite.
- Letting a number be a linear function (other than the sum) of the 2 preceding numbers. The Pell numbers have Pn = 2Pn−1 + Pn−2. If the coefficient of the preceding value is assigned a variable value x, the result is the sequence of Fibonacci polynomials.
- Not adding the immediately preceding numbers. The Padovan sequence and Perrin numbers have P(n) = P(n − 2) + P(n − 3).
- Generating the next number by adding 3 numbers (tribonacci numbers), 4 numbers (tetranacci numbers), or more. The resulting sequences are known as n-Step Fibonacci numbers.[64]
Applications[edit]
Mathematics[edit]

The Fibonacci numbers occur as the sums of binomial coefficients in the "shallow" diagonals of Pascal's triangle:[65]
To see how the formula is used, we can arrange the sums by the number of terms present:
5 = 1+1+1+1+1 = 2+1+1+1 = 1+2+1+1 = 1+1+2+1 = 1+1+1+2 = 2+2+1 = 2+1+2 = 1+2+2
which is , where we are choosing the positions of k twos from n−k−1 terms.

These numbers also give the solution to certain enumerative problems,[66] the most common of which is that of counting the number of ways of writing a given number n as an ordered sum of 1s and 2s (called compositions); there are Fn+1 ways to do this (equivalently, it's also the number of domino tilings of the rectangle). For example, there are F5+1 = F6 = 8 ways one can climb a staircase of 5 steps, taking one or two steps at a time:
5 = 1+1+1+1+1 = 2+1+1+1 = 1+2+1+1 = 1+1+2+1 = 2+2+1 = 1+1+1+2 = 2+1+2 = 1+2+2
The figure shows that 8 can be decomposed into 5 (the number of ways to climb 4 steps, followed by a single-step) plus 3 (the number of ways to climb 3 steps, followed by a double-step). The same reasoning is applied recursively until a single step, of which there is only one way to climb.
The Fibonacci numbers can be found in different ways among the set of binary strings, or equivalently, among the subsets of a given set.
- The number of binary strings of length n without consecutive 1s is the Fibonacci number Fn+2. For example, out of the 16 binary strings of length 4, there are F6 = 8 without consecutive 1s – they are 0000, 0001, 0010, 0100, 0101, 1000, 1001, and 1010. Such strings are the binary representations of Fibbinary numbers. Equivalently, Fn+2 is the number of subsets S of {1, ..., n} without consecutive integers, that is, those S for which {i, i + 1} ⊈ S for every i. A bijection with the sums to n+1 is to replace 1 with 0 and 2 with 10, and drop the last zero.
- The number of binary strings of length n without an odd number of consecutive 1s is the Fibonacci number Fn+1. For example, out of the 16 binary strings of length 4, there are F5 = 5 without an odd number of consecutive 1s – they are 0000, 0011, 0110, 1100, 1111. Equivalently, the number of subsets S of {1, ..., n} without an odd number of consecutive integers is Fn+1. A bijection with the sums to n is to replace 1 with 0 and 2 with 11.
- The number of binary strings of length n without an even number of consecutive 0s or 1s is 2Fn. For example, out of the 16 binary strings of length 4, there are 2F4 = 6 without an even number of consecutive 0s or 1s – they are 0001, 0111, 0101, 1000, 1010, 1110. There is an equivalent statement about subsets.
- Yuri Matiyasevich was able to show that the Fibonacci numbers can be defined by a Diophantine equation, which led to his solving Hilbert's tenth problem.[67]
- The Fibonacci numbers are also an example of a complete sequence. This means that every positive integer can be written as a sum of Fibonacci numbers, where any one number is used once at most.
- Moreover, every positive integer can be written in a unique way as the sum of one or more distinct Fibonacci numbers in such a way that the sum does not include any two consecutive Fibonacci numbers. This is known as Zeckendorf's theorem, and a sum of Fibonacci numbers that satisfies these conditions is called a Zeckendorf representation. The Zeckendorf representation of a number can be used to derive its Fibonacci coding.
- Starting with 5, every second Fibonacci number is the length of the hypotenuse of a right triangle with integer sides, or in other words, the largest number in a Pythagorean triple, obtained from the formula The sequence of Pythagorean triangles obtained from this formula has sides of lengths (3,4,5), (5,12,13), (16,30,34), (39,80,89), ... . The middle side of each of these triangles is the sum of the three sides of the preceding triangle.[68]
- The Fibonacci cube is an undirected graph with a Fibonacci number of nodes that has been proposed as a network topology for parallel computing.
- Fibonacci numbers appear in the ring lemma, used to prove connections between the circle packing theorem and conformal maps.[69]
Computer science[edit]

The keys in the left spine are Fibonacci numbers.
- The Fibonacci numbers are important in computational run-time analysis of Euclid's algorithm to determine the greatest common divisor of two integers: the worst case input for this algorithm is a pair of consecutive Fibonacci numbers.[70]
- Fibonacci numbers are used in a polyphase version of the merge sort algorithm in which an unsorted list is divided into two lists whose lengths correspond to sequential Fibonacci numbers – by dividing the list so that the two parts have lengths in the approximate proportion φ. A tape-drive implementation of the polyphase merge sort was described in The Art of Computer Programming.
- A Fibonacci tree is a binary tree whose child trees (recursively) differ in height by exactly 1. So it is an AVL tree, and one with the fewest nodes for a given height — the "thinnest" AVL tree. These trees have a number of vertices that is a Fibonacci number minus one, an important fact in the analysis of AVL trees.[71]
- Fibonacci numbers are used by some pseudorandom number generators.
- Fibonacci numbers arise in the analysis of the Fibonacci heap data structure.
- A one-dimensional optimization method, called the Fibonacci search technique, uses Fibonacci numbers.[72]
- The Fibonacci number series is used for optional lossy compression in the IFF 8SVX audio file format used on Amiga computers. The number series compands the original audio wave similar to logarithmic methods such as μ-law.[73][74]
- Some Agile teams use a modified series called the "Modified Fibonacci Series" in planning poker, as an estimation tool. Planning Poker is a formal part of the Scaled Agile Framework.[75]
- Fibonacci coding
- Negafibonacci coding
Nature[edit]

Fibonacci sequences appear in biological settings,[76] such as branching in trees, arrangement of leaves on a stem, the fruitlets of a pineapple,[77] the flowering of artichoke, and the arrangement of a pine cone,[78] and the family tree of honeybees.[79][80] Kepler pointed out the presence of the Fibonacci sequence in nature, using it to explain the (golden ratio-related) pentagonal form of some flowers.[81] Field daisies most often have petals in counts of Fibonacci numbers.[82] In 1830, K. F. Schimper and A. Braun discovered that the parastichies (spiral phyllotaxis) of plants were frequently expressed as fractions involving Fibonacci numbers.[83]
Przemysław Prusinkiewicz advanced the idea that real instances can in part be understood as the expression of certain algebraic constraints on free groups, specifically as certain Lindenmayer grammars.[84]

A model for the pattern of florets in the head of a sunflower was proposed by Helmut Vogel in 1979.[85] This has the form
where n is the index number of the floret and c is a constant scaling factor; the florets thus lie on Fermat's spiral. The divergence angle, approximately 137.51°, is the golden angle, dividing the circle in the golden ratio. Because this ratio is irrational, no floret has a neighbor at exactly the same angle from the center, so the florets pack efficiently. Because the rational approximations to the golden ratio are of the form F( j):F( j + 1), the nearest neighbors of floret number n are those at n ± F( j) for some index j, which depends on r, the distance from the center. Sunflowers and similar flowers most commonly have spirals of florets in clockwise and counter-clockwise directions in the amount of adjacent Fibonacci numbers,[86] typically counted by the outermost range of radii.[87]
Fibonacci numbers also appear in the pedigrees of idealized honeybees, according to the following rules:
- If an egg is laid by an unmated female, it hatches a male or drone bee.
- If, however, an egg was fertilized by a male, it hatches a female.
Thus, a male bee always has one parent, and a female bee has two. If one traces the pedigree of any male bee (1 bee), he has 1 parent (1 bee), 2 grandparents, 3 great-grandparents, 5 great-great-grandparents, and so on. This sequence of numbers of parents is the Fibonacci sequence. The number of ancestors at each level, Fn, is the number of female ancestors, which is Fn−1, plus the number of male ancestors, which is Fn−2.[88] This is under the unrealistic assumption that the ancestors at each level are otherwise unrelated.

It has been noticed that the number of possible ancestors on the human X chromosome inheritance line at a given ancestral generation also follows the Fibonacci sequence.[89] A male individual has an X chromosome, which he received from his mother, and a Y chromosome, which he received from his father. The male counts as the "origin" of his own X chromosome (), and at his parents' generation, his X chromosome came from a single parent (). The male's mother received one X chromosome from her mother (the son's maternal grandmother), and one from her father (the son's maternal grandfather), so two grandparents contributed to the male descendant's X chromosome (). The maternal grandfather received his X chromosome from his mother, and the maternal grandmother received X chromosomes from both of her parents, so three great-grandparents contributed to the male descendant's X chromosome (). Five great-great-grandparents contributed to the male descendant's X chromosome (), etc. (This assumes that all ancestors of a given descendant are independent, but if any genealogy is traced far enough back in time, ancestors begin to appear on multiple lines of the genealogy, until eventually a population founder appears on all lines of the genealogy.)
Other[edit]
- In optics, when a beam of light shines at an angle through two stacked transparent plates of different materials of different refractive indexes, it may reflect off three surfaces: the top, middle, and bottom surfaces of the two plates. The number of different beam paths that have k reflections, for k > 1, is the th Fibonacci number. (However, when k = 1, there are three reflection paths, not two, one for each of the three surfaces.)[90]
- Fibonacci retracement levels are widely used in technical analysis for financial market trading.
- Since the conversion factor 1.609344 for miles to kilometers is close to the golden ratio, the decomposition of distance in miles into a sum of Fibonacci numbers becomes nearly the kilometer sum when the Fibonacci numbers are replaced by their successors. This method amounts to a radix 2 number register in golden ratio base φ being shifted. To convert from kilometers to miles, shift the register down the Fibonacci sequence instead.[91]
- The measured values of voltages and currents in the infinite resistor chain circuit (also called the resistor ladder or infinite series-parallel circuit) follow the Fibonacci sequence. The intermediate results of adding the alternating series and parallel resistances yields fractions composed of consecutive Fibonacci numbers. The equivalent resistance of the entire circuit equals the golden ratio.[92]
- Brasch et al. 2012 show how a generalized Fibonacci sequence also can be connected to the field of economics.[93] In particular, it is shown how a generalized Fibonacci sequence enters the control function of finite-horizon dynamic optimisation problems with one state and one control variable. The procedure is illustrated in an example often referred to as the Brock–Mirman economic growth model.
- Mario Merz included the Fibonacci sequence in some of his artworks beginning in 1970.[94]
- Joseph Schillinger (1895–1943) developed a system of composition which uses Fibonacci intervals in some of its melodies; he viewed these as the musical counterpart to the elaborate harmony evident within nature.[95] See also Golden ratio § Music.
See also[edit]
- The Fibonacci Association – Organization for research on Fibonacci numbers
- Fibonacci numbers in popular culture
- Fibonacci word – Binary sequence from Fibonacci recurrence
- Random Fibonacci sequence – Randomized mathematical sequence based upon the Fibonacci sequence
- Wythoff array – Infinite matrix of integers derived from the Fibonacci sequence
References[edit]
Explanatory footnotes[edit]
- ^ "For four, variations of meters of two [and] three being mixed, five happens. For five, variations of two earlier – three [and] four, being mixed, eight is obtained. In this way, for six, [variations] of four [and] of five being mixed, thirteen happens. And like that, variations of two earlier meters being mixed, seven morae [is] twenty-one. In this way, the process should be followed in all mātrā-vṛttas" [13]
Citations[edit]
- ^ a b Sloane, N. J. A. (ed.), "Sequence A000045", The On-Line Encyclopedia of Integer Sequences, OEIS Foundation
- ^ a b c Goonatilake, Susantha (1998), Toward a Global Science, Indiana University Press, p. 126, ISBN 978-0-253-33388-9
- ^ a b Singh, Parmanand (1985), "The So-called Fibonacci numbers in ancient and medieval India", Historia Mathematica, 12 (3): 229–44, doi:10.1016/0315-0860(85)90021-7
- ^ a b Knuth, Donald (2006), The Art of Computer Programming, vol. 4. Generating All Trees – History of Combinatorial Generation, Addison–Wesley, p. 50, ISBN 978-0-321-33570-8,
it was natural to consider the set of all sequences of [L] and [S] that have exactly m beats. ...there are exactly Fm+1 of them. For example the 21 sequences when m = 7 are: [gives list]. In this way Indian prosodists were led to discover the Fibonacci sequence, as we have observed in Section 1.2.8 (from v.1)
- ^ Sigler 2002, pp. 404–05.
- ^ Lucas 1891, p. 3.
- ^ Beck & Geoghegan 2010.
- ^ Bóna 2011, p. 180.
- ^ Knuth, Donald (1968), The Art of Computer Programming, vol. 1, Addison Wesley, p. 100, ISBN 978-81-7758-754-8,
Before Fibonacci wrote his work, the sequence Fn had already been discussed by Indian scholars, who had long been interested in rhythmic patterns... both Gopala (before 1135 AD) and Hemachandra (c. 1150) mentioned the numbers 1,2,3,5,8,13,21 explicitly [see P. Singh Historia Math 12 (1985) 229–44]" p. 100 (3d ed)...
- ^ a b Livio 2003, p. 197.
- ^ Agrawala, VS (1969), Pāṇinikālīna Bhāratavarṣa (Hn.). Varanasi-I: TheChowkhamba Vidyabhawan,
SadgurushiShya writes that Pingala was a younger brother of Pāṇini [Agrawala 1969, lb]. There is an alternative opinion that he was a maternal uncle of Pāṇini [Vinayasagar 1965, Preface, 121]. ... Agrawala [1969, 463–76], after a careful investigation, in which he considered the views of earlier scholars, has concluded that Pāṇini lived between 480 and 410 BC
- ^ Singh, Parmanand (1985), "The So-called Fibonacci Numbers in Ancient and Medieval India", Historia Mathematica, Academic Press, 12 (3): 232, doi:10.1016/0315-0860(85)90021-7
- ^ Velankar, HD (1962), 'Vṛttajātisamuccaya' of kavi Virahanka, Jodhpur: Rajasthan Oriental Research Institute, p. 101
- ^ Livio 2003, p. 197–198.
- ^ Shah, Jayant (1991), "A History of Piṅgala's Combinatorics" (PDF), Northeastern University: 41, retrieved 4 January 2019
- ^ Sigler 2002, pp. 404–405.
- ^ "Fibonacci's Liber Abaci (Book of Calculation)", The University of Utah, 13 December 2009, retrieved 28 November 2018
- ^ Hemenway, Priya (2005), Divine Proportion: Phi In Art, Nature, and Science, New York: Sterling, pp. 20–21, ISBN 1-4027-3522-7
- ^ Knott, Dr. Ron (25 September 2016), "The Fibonacci Numbers and Golden section in Nature – 1", University of Surrey, retrieved 27 November 2018
- ^ Knott, Ron, Fibonacci's Rabbits, University of Surrey Faculty of Engineering and Physical Sciences
- ^ Gardner, Martin (1996), Mathematical Circus, The Mathematical Association of America, p. 153, ISBN 978-0-88385-506-5,
It is ironic that Leonardo, who made valuable contributions to mathematics, is remembered today mainly because a 19th-century French number theorist, Édouard Lucas... attached the name Fibonacci to a number sequence that appears in a trivial problem in Liber abaci
- ^ Beutelspacher, Albrecht; Petri, Bernhard (1996), "Fibonacci-Zahlen", Der Goldene Schnitt, Vieweg+Teubner Verlag, pp. 87–98, doi:10.1007/978-3-322-85165-9_6
- ^ Ball 2003, p. 156.
- ^ Ball 2003, pp. 155–156.
- ^ Sloane, N. J. A. (ed.), "Sequence A002390", The On-Line Encyclopedia of Integer Sequences, OEIS Foundation
- ^ Sloane, N. J. A. (ed.), "Sequence A097348", The On-Line Encyclopedia of Integer Sequences, OEIS Foundation
- ^ Kepler, Johannes (1966), A New Year Gift: On Hexagonal Snow, Oxford University Press, p. 92, ISBN 978-0-19-858120-8
- ^ Strena seu de Nive Sexangula, 1611
- ^ Gessel, Ira (October 1972), "Fibonacci is a Square" (PDF), The Fibonacci Quarterly, 10 (4): 417–19, retrieved April 11, 2012
- ^ Dijkstra, Edsger W. (1978), In honour of Fibonacci (PDF)
- ^ Lucas 1891, p. 4.
- ^ Vorobiev, Nikolaĭ Nikolaevich; Martin, Mircea (2002), "Chapter 1", Fibonacci Numbers, Birkhäuser, pp. 5–6, ISBN 978-3-7643-6135-8
- ^ Flajolet, Philippe; Sedgewick, Robert (2009), Analytic Combinatorics, Cambridge University Press, p. 42, ISBN 978-0521898065
- ^ a b c Weisstein, Eric W., "Fibonacci Number", MathWorld
- ^ Glaister, P (1995), "Fibonacci power series", The Mathematical Gazette, 79 (486): 521–25, doi:10.2307/3618079, JSTOR 3618079, S2CID 116536130
- ^ Landau (1899) quoted according Borwein, Page 95, Exercise 3b.
- ^ Sloane, N. J. A. (ed.), "Sequence A079586", The On-Line Encyclopedia of Integer Sequences, OEIS Foundation
- ^ André-Jeannin, Richard (1989), "Irrationalité de la somme des inverses de certaines suites récurrentes", Comptes Rendus de l'Académie des Sciences, Série I, 308 (19): 539–41, MR 0999451
- ^ Honsberger, Ross (1985), "Millin's series", Mathematical Gems III, Dolciani Mathematical Expositions, vol. 9, American Mathematical Society, pp. 135–136, ISBN 9781470457181
- ^ Ribenboim, Paulo (2000), My Numbers, My Friends, Springer-Verlag
- ^ Su, Francis E (2000), "Fibonacci GCD's, please", Mudd Math Fun Facts, et al, HMC, archived from the original on 2009-12-14, retrieved 2007-02-23
- ^ Williams, H. C. (1982), "A note on the Fibonacci quotient ", Canadian Mathematical Bulletin, 25 (3): 366–70, doi:10.4153/CMB-1982-053-0, hdl:10338.dmlcz/137492, MR 0668957. Williams calls this property "well known".
- ^ Prime Numbers, Richard Crandall, Carl Pomerance, Springer, second edition, 2005, p. 142.
- ^ Sloane, N. J. A. (ed.), "Sequence A005478", The On-Line Encyclopedia of Integer Sequences, OEIS Foundation
- ^ Diaconis, Persi (2018), "Probabilizing Fibonacci numbers" (PDF), in Butler, Steve; Cooper, Joshua; Hurlbert, Glenn (eds.), Connections in Discrete Mathematics: A Celebration of the Work of Ron Graham, Cambridge University Press, pp. 1–12, ISBN 978-1-107-15398-1, MR 3821829
- ^ Honsberger, Ross (1985), "Mathematical Gems III", AMS Dolciani Mathematical Expositions (9): 133, ISBN 978-0-88385-318-4
- ^ Cohn, J. H. E. (1964), "On square Fibonacci numbers", The Journal of the London Mathematical Society, 39: 537–540, doi:10.1112/jlms/s1-39.1.537, MR 0163867
- ^ Pethő, Attila (2001), "Diophantine properties of linear recursive sequences II", Acta Mathematica Academiae Paedagogicae Nyíregyháziensis, 17: 81–96
- ^ Bugeaud, Y; Mignotte, M; Siksek, S (2006), "Classical and modular approaches to exponential Diophantine equations. I. Fibonacci and Lucas perfect powers", Ann. Math., 2 (163): 969–1018, arXiv:math/0403046, Bibcode:2004math......3046B, doi:10.4007/annals.2006.163.969, S2CID 10266596
- ^ Luo, Ming (1989), "On triangular Fibonacci numbers" (PDF), Fibonacci Quart., 27 (2): 98–108
- ^ Luca, Florian (2000), "Perfect Fibonacci and Lucas numbers", Rendiconti del Circolo Matematico di Palermo, 49 (2): 313–18, doi:10.1007/BF02904236, ISSN 1973-4409, MR 1765401, S2CID 121789033
- ^ Broughan, Kevin A.; González, Marcos J.; Lewis, Ryan H.; Luca, Florian; Mejía Huguet, V. Janitzio; Togbé, Alain (2011), "There are no multiply-perfect Fibonacci numbers", Integers, 11a: A7, MR 2988067
- ^ Luca, Florian; Mejía Huguet, V. Janitzio (2010), "On Perfect numbers which are ratios of two Fibonacci numbers", Annales Mathematicae at Informaticae, 37: 107–24, ISSN 1787-6117, MR 2753031
- ^ Knott, Ron, The Fibonacci numbers, UK: Surrey
- ^ Sloane, N. J. A. (ed.), "Sequence A235383", The On-Line Encyclopedia of Integer Sequences, OEIS Foundation
- ^ Ribenboim, Paulo (1996), The New Book of Prime Number Records, New York: Springer, p. 64, ISBN 978-0-387-94457-9
- ^ Lemmermeyer 2000, pp. 73–74, ex. 2.25–28.
- ^ Lemmermeyer 2000, pp. 73–74, ex. 2.28.
- ^ Lemmermeyer 2000, p. 73, ex. 2.27.
- ^ Fibonacci and Lucas factorizations, Mersennus collects all known factors of F(i) with i < 10000.
- ^ Factors of Fibonacci and Lucas numbers, Red golpe collects all known factors of F(i) with 10000 < i < 50000.
- ^ Freyd, Peter; Brown, Kevin S. (1993), "Problems and Solutions: Solutions: E3410", The American Mathematical Monthly, 99 (3): 278–79, doi:10.2307/2325076, JSTOR 2325076
- ^ Sloane, N. J. A. (ed.), "Sequence A001175", The On-Line Encyclopedia of Integer Sequences, OEIS Foundation
- ^ Lü, Kebo; Wang, Jun (2006), "k-step Fibonacci sequence modulo m", Utilitas Mathematica, 71: 169–177, MR 2278830
- ^ Lucas 1891, p. 7.
- ^ Stanley, Richard (2011), Enumerative Combinatorics I (2nd ed.), Cambridge Univ. Press, p. 121, Ex 1.35, ISBN 978-1-107-60262-5
- ^ Harizanov, Valentina (1995), "Review of Yuri V. Matiyasevich, Hibert's Tenth Problem", Modern Logic, 5 (3): 345–55
- ^ Pagni, David (September 2001), "Fibonacci Meets Pythagoras", Mathematics in School, 30 (4): 39–40, JSTOR 30215477
- ^ Stephenson, Kenneth (2005), Introduction to Circle Packing: The Theory of Discrete Analytic Functions, Cambridge University Press, ISBN 978-0-521-82356-2, MR 2131318; see especially Lemma 8.2 (Ring Lemma), pp. 73–74, and Appendix B, The Ring Lemma, pp. 318–321.
- ^ Knuth, Donald E (1997), The Art of Computer Programming, vol. 1: Fundamental Algorithms (3rd ed.), Addison–Wesley, p. 343, ISBN 978-0-201-89683-1
- ^ Adelson-Velsky, Georgy; Landis, Evgenii (1962), "An algorithm for the organization of information", Proceedings of the USSR Academy of Sciences (in Russian), 146: 263–266 English translation by Myron J. Ricci in Soviet Mathematics - Doklady, 3:1259–1263, 1962.
- ^ Avriel, M; Wilde, DJ (1966), "Optimality of the Symmetric Fibonacci Search Technique", Fibonacci Quarterly (3): 265–69
- ^ Amiga ROM Kernel Reference Manual, Addison–Wesley, 1991
- ^ "IFF", Multimedia Wiki
- ^ Dean Leffingwell (2021-07-01), Story, Scaled Agile Framework, retrieved 2022-08-15
- ^ Douady, S; Couder, Y (1996), "Phyllotaxis as a Dynamical Self Organizing Process" (PDF), Journal of Theoretical Biology, 178 (3): 255–74, doi:10.1006/jtbi.1996.0026, archived from the original (PDF)on 2006-05-26
- ^ Jones, Judy; Wilson, William (2006), "Science", An Incomplete Education, Ballantine Books, p. 544, ISBN 978-0-7394-7582-9
- ^ Brousseau, A (1969), "Fibonacci Statistics in Conifers", Fibonacci Quarterly (7): 525–32
- ^ "Marks for the da Vinci Code: B–", Maths, Computer Science For Fun: CS4FN
- ^ Scott, T.C.; Marketos, P. (March 2014), On the Origin of the Fibonacci Sequence (PDF), MacTutor History of Mathematics archive, University of St Andrews
- ^ Livio 2003, p. 110.
- ^ Livio 2003, pp. 112–13.
- ^ Varenne, Franck (2010), Formaliser le vivant - Lois, Théories, Modèles(in French), Hermann, p. 28, ISBN 9782705678128, retrieved 2022-10-30,
En 1830, K. F. Schimper et A. Braun [...]. Ils montraient que si l'on représente cet angle de divergence par une fraction reflétant le nombre de tours par feuille ([...]), on tombe régulièrement sur un des nombres de la suite de Fibonacci pour le numérateur [...].
- ^ Prusinkiewicz, Przemyslaw; Hanan, James (1989), Lindenmayer Systems, Fractals, and Plants (Lecture Notes in Biomathematics), Springer-Verlag, ISBN 978-0-387-97092-9
- ^ Vogel, Helmut (1979), "A better way to construct the sunflower head", Mathematical Biosciences, 44 (3–4): 179–89, doi:10.1016/0025-5564(79)90080-4
- ^ Livio 2003, p. 112.
- ^ Prusinkiewicz, Przemyslaw; Lindenmayer, Aristid (1990), "4", The Algorithmic Beauty of Plants, Springer-Verlag, pp. 101–107, ISBN 978-0-387-97297-8
- ^ "The Fibonacci sequence as it appears in nature" (PDF), The Fibonacci Quarterly, 1 (1): 53–56, 1963
- ^ a b Hutchison, Luke (September 2004), "Growing the Family Tree: The Power of DNA in Reconstructing Family Relationships" (PDF), Proceedings of the First Symposium on Bioinformatics and Biotechnology (BIOT-04), retrieved 2016-09-03
- ^ Livio 2003, pp. 98–99.
- ^ "Zeckendorf representation", Encyclopedia of Math
- ^ Patranabis, D.; Dana, S. K. (December 1985), "Single-shunt fault diagnosis through terminal attenuation measurement and using Fibonacci numbers", IEEE Transactions on Instrumentation and Measurement, IM-34 (4): 650–653, Bibcode:1985ITIM...34..650P, doi:10.1109/tim.1985.4315428, S2CID 35413237
- ^ Brasch, T. von; Byström, J.; Lystad, L.P. (2012), "Optimal Control and the Fibonacci Sequence", Journal of Optimization Theory and Applications, 154 (3): 857–78, doi:10.1007/s10957-012-0061-2, hdl:11250/180781, S2CID 8550726
- ^ Livio 2003, p. 176.
- ^ Livio 2003, p. 193.
Works cited[edit]
- Ball, Keith M (2003), "8: Fibonacci's Rabbits Revisited", Strange Curves, Counting Rabbits, and Other Mathematical Explorations, Princeton, NJ: Princeton University Press, ISBN 978-0-691-11321-0.
- Beck, Matthias; Geoghegan, Ross (2010), The Art of Proof: Basic Training for Deeper Mathematics, New York: Springer, ISBN 978-1-4419-7022-0.
- Bóna, Miklós (2011), A Walk Through Combinatorics (3rd ed.), New Jersey: World Scientific, ISBN 978-981-4335-23-2.
- Borwein, Jonathan M.; Borwein, Peter B. (July 1998), Pi and the AGM: A Study in Analytic Number Theory and Computational Complexity, Wiley, pp. 91–101, ISBN 978-0-471-31515-5
- Lemmermeyer, Franz (2000), Reciprocity Laws: From Euler to Eisenstein, Springer Monographs in Mathematics, New York: Springer, ISBN 978-3-540-66957-9.
- Livio, Mario (2003) [2002], The Golden Ratio: The Story of Phi, the World's Most Astonishing Number (First trade paperback ed.), New York City: Broadway Books, ISBN 0-7679-0816-3
- Lucas, Édouard (1891), Théorie des nombres (in French), vol. 1, Paris: Gauthier-Villars.
- Sigler, L. E. (2002), Fibonacci's Liber Abaci: A Translation into Modern English of Leonardo Pisano's Book of Calculation, Sources and Studies in the History of Mathematics and Physical Sciences, Springer, ISBN 978-0-387-95419-6
External links[edit]
- Sunflowers and Fibonacci - Numberphile on YouTube
- Periods of Fibonacci Sequences Mod m at MathPages
- Scientists find clues to the formation of Fibonacci spirals in nature
- Fibonacci Sequence on In Our Time at the BBC
- "Fibonacci numbers", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- OEIS sequence A000045 (Fibonacci numbers)
Morse code


Morse code is a method used in telecommunication to encode text characters as standardized sequences of two different signal durations, called dots and dashes, or dits and dahs.[3][4] Morse code is named after Samuel Morse, one of the inventors of the telegraph.
International Morse code encodes the 26 basic Latin letters a through z, one accented Latin letter (é), the Arabic numerals, and a small set of punctuation and procedural signals (prosigns). There is no distinction between upper and lower case letters.[1] Each Morse code symbol is formed by a sequence of dits and dahs. The dit duration is the basic unit of time measurement in Morse code transmission. The duration of a dah is three times the duration of a dit. Each dit or dah within an encoded character is followed by a period of signal absence, called a space, equal to the dit duration. The letters of a word are separated by a space of duration equal to three dits, and words are separated by a space equal to seven dits.[1][5][a]
Morse code can be memorized and sent in a form perceptible to the human senses, e.g. via sound waves or visible light, such that it can be directly interpreted by persons trained in the skill.[7][8] Morse code is usually transmitted by on-off keying of an information-carrying medium such as electric current, radio waves, visible light, or sound waves.[9][10] The current or wave is present during the time period of the dit or dah and absent during the time between dits and dahs.[11][12]
Since many natural languages use more than the 26 letters of the Latin alphabet, Morse alphabets have been developed for those languages, largely by transliteration of existing codes.[13]
To increase the efficiency of encoding, Morse code was originally designed so that the length of each symbol is approximately inverse to the frequency of occurrence of the character that it represents in text of the English language. Thus the most common letter in English, the letter e, has the shortest code – a single dit. Because the Morse code elements are specified by proportion rather than specific time durations, the code is usually transmitted at the highest rate that the receiver is capable of decoding. Morse code transmission rate (speed) is specified in groups per minute, commonly referred to as words per minute.[b][7]
Development and history
Pre-Morse telegraphs and codes

Early in the nineteenth century, European experimenters made progress with electrical signaling systems, using a variety of techniques including static electricity and electricity from Voltaic pilesproducing electrochemical and electromagnetic changes. These experimental designs were precursors to practical telegraphic applications.[14]

Following the discovery of electromagnetism by Hans Christian Ørsted in 1820 and the invention of the electromagnet by William Sturgeon in 1824, there were developments in electromagnetic telegraphy in Europe and America. Pulses of electric current were sent along wires to control an electromagnet in the receiving instrument. Many of the earliest telegraph systems used a single-needle system which gave a very simple and robust instrument. However, it was slow, as the receiving operator had to alternate between looking at the needle and writing down the message. In Morse code, a deflection of the needle to the left corresponded to a dit and a deflection to the right to a dah.[15] By making the two clicks sound different with one ivory and one metal stop, the single needle device became an audible instrument, which led in turn to the Double Plate Sounder System.[16]
William Cooke and Charles Wheatstone in Britain developed an electrical telegraph that used electromagnets in its receivers. They obtained an English patent in June 1837 and demonstrated it on the London and Birmingham Railway, making it the first commercial telegraph. Carl Friedrich Gauss and Wilhelm Eduard Weber (1833) as well as Carl August von Steinheil (1837) used codes with varying word lengths for their telegraph systems.[17] In 1841, Cooke and Wheatstone built a telegraph that printed the letters from a wheel of typefaces struck by a hammer.[18]: 79
Samuel Morse and Alfred Vail

The American artist Samuel Morse, the American physicist Joseph Henry, and mechanical engineer Alfred Vaildeveloped an electrical telegraph system. It needed a method to transmit natural language using only electrical pulses and the silence between them. Around 1837, Morse therefore developed an early forerunner to the modern International Morse code.[18]: 79
The Morse system for telegraphy, which was first used in about 1844, was designed to make indentations on a paper tape when electric currents were received. Morse's original telegraph receiver used a mechanical clockwork to move a paper tape. When an electrical current was received, an electromagnet engaged an armature that pushed a stylus onto the moving paper tape, making an indentation on the tape. When the current was interrupted, a spring retracted the stylus and that portion of the moving tape remained unmarked. Morse code was developed so that operators could translate the indentations marked on the paper tape into text messages.
In his earliest design for a code, Morse had planned to transmit only numerals, and to use a codebook to look up each word according to the number which had been sent. However, the code was soon expanded by Alfred Vail in 1840 to include letters and special characters, so it could be used more generally. Vail estimated the frequency of use of letters in the English language by counting the movable type he found in the type-cases of a local newspaper in Morristown, New Jersey.[18]: 84 The shorter marks were called "dots" and the longer ones "dashes", and the letters most commonly used were assigned the shortest sequences of dots and dashes. This code, first used in 1844, became known as Morse landline code, American Morse code, or Railroad Morse, until the end of railroad telegraphy in the U.S. in the 1970s.[citation needed]
Operator-led change from graphical to audible code
In the original Morse telegraph system, the receiver's armature made a clicking noise as it moved in and out of position to mark the paper tape. The telegraph operators soon learned that they could translate the clicks directly into dots and dashes, and write these down by hand, thus making the paper tape unnecessary. When Morse code was adapted to radio communication, the dots and dashes were sent as short and long tone pulses. It was later found that people become more proficient at receiving Morse code when it is taught as a language that is heard, instead of one read from a page.[19]
With the advent of tones produced by radiotelegraph receivers, the operators began to vocalize a dot as dit, and a dash as dah, to reflect the sounds of Morse code they heard. To conform to normal sending speed, dits which are not the last element of a code became voiced as di. For example, the letter lis voiced as di dah di dit.[20][21] Morse code was sometimes facetiously known as "iddy-umpty", a dit lampooned as "iddy" and a dah as "umpty", leading to the word "umpteen".[22]

Gerke's refinement of Morse's code
The Morse code, as specified in the current international standard, International Morse Code Recommendation, ITU-R M.1677-1,[1] was derived from a much-improved proposal by Friedrich Gerke in 1848 that became known as the "Hamburg alphabet".
Gerke changed many of the codepoints, in the process doing away with the different length dashes and different inter-element spaces of American Morse, leaving only two coding elements, the dot and the dash. Codes for German umlauted vowels and ch were introduced. Gerke's code was adopted in Germany and Austria 1851.[23]
This finally led to the International Morse code in 1865. The International Morse code adopted most of Gerke's codepoints. The codes for o and p were taken from a code system developed by Steinheil. A new codepoint was added for j since Gerke did not distinguish between i and j. Changes were also made to x, y, and z. This left only four codepoints identical to the original Morse code, namely e, h, k and n, and the latter two had their dahs extended to full length. The original American code being compared dates to 1838; the later American code shown in the table was developed in 1844.[17]
Radiotelegraphy and aviation
In the 1890s, Morse code began to be used extensively for early radio communication before it was possible to transmit voice. In the late 19th and early 20th centuries, most high-speed international communication used Morse code on telegraph lines, undersea cables, and radio circuits.
Although previous transmitters were bulky and the spark gap system of transmission was dangerous and difficult to use, there had been some early attempts: In 1910, the U.S. Navy experimented with sending Morse from an airplane.[24] However the first regular aviation radiotelegraphy was on airships, which had space to accommodate the large, heavy radio equipment then in use. The same year, 1910, a radio on the airship America was instrumental in coordinating the rescue of its crew.[25]
During World War I, Zeppelin airships equipped with radio were used for bombing and naval scouting,[26] and ground-based radio direction finders were used for airship navigation.[26] Allied airships and military aircraft also made some use of radiotelegraphy.
However, there was little aeronautical radio in general use during World War I, and in the 1920s, there was no radio system used by such important flights as that of Charles Lindbergh from New York to Paris in 1927. Once he and the Spirit of St. Louis were off the ground, Lindbergh was truly incommunicado and alone. Morse code in aviation began regular use in the mid-1920s. By 1928, when the first airplane flight was made by the Southern Cross from California to Australia, one of its four crewmen was a radio operator who communicated with ground stations via radio telegraph.
Beginning in the 1930s, both civilian and military pilots were required to be able to use Morse code, both for use with early communications systems and for identification of navigational beacons that transmitted continuous two- or three-letter identifiers in Morse code. Aeronautical charts show the identifier of each navigational aid next to its location on the map.
In addition, rapidly moving field armies could not have fought effectively without radiotelegraphy; they moved more quickly than their communications services could put up new telegraph and telephone lines. This was seen especially in the blitzkrieg offensives of the Nazi German Wehrmacht in Poland, Belgium, France (in 1940), the Soviet Union, and in North Africa; by the British Army in North Africa, Italy, and the Netherlands; and by the U.S. Army in France and Belgium (in 1944), and in southern Germany in 1945.
Maritime flash telegraphy and radio telegraphy

Radiotelegraphy using Morse code was vital during World War II, especially in carrying messages between the warships and the naval bases of the belligerents. Long-range ship-to-ship communication was by radio telegraphy, using encrypted messages because the voice radio systems on ships then were quite limited in both their range and their security. Radiotelegraphy was also extensively used by warplanes, especially by long-range patrol planesthat were sent out by those navies to scout for enemy warships, cargo ships, and troop ships.
Morse code was used as an international standard for maritime distress until 1999 when it was replaced by the Global Maritime Distress and Safety System. When the French Navy ceased using Morse code on January 31, 1997, the final message transmitted was "Calling all. This is our last cry before our eternal silence."[27]
Demise of commercial telegraphy
In the United States the final commercial Morse code transmission was on July 12, 1999, signing off with Samuel Morse's original 1844 message, what hath god wrought, and the prosign sk ("end of contact").[28]
As of 2015, the United States Air Force still trains ten people a year in Morse.[29]
The United States Coast Guard has ceased all use of Morse code on the radio, and no longer monitors any radio frequencies for Morse code transmissions, including the international medium frequency (MF) distress frequency of 500 kHz.[30] However, the Federal Communications Commissionstill grants commercial radiotelegraph operator licenses to applicants who pass its code and written tests.[31] Licensees have reactivated the old California coastal Morse station KPH and regularly transmit from the site under either this call sign or as KSM. Similarly, a few U.S. museum ship stations are operated by Morse enthusiasts.[32]
Operator proficiency

Morse code speed is measured in words per minute (wpm) or characters per minute (cpm). Characters have differing lengths because they contain differing numbers of dits and dahs. Consequently, words also have different lengths in terms of dot duration, even when they contain the same number of characters. For this reason, a standard word is helpful to measure operator transmission speed. paris and codex are two such standard words.[33] Operators skilled in Morse code can often understand ("copy") code in their heads at rates in excess of 40 wpm.
In addition to knowing, understanding, and being able to copy the standard written alpha-numeric and punctuation characters or symbols at high speeds, skilled high speed operators must also be fully knowledgeable of all of the special unwritten Morse code symbols for the standard Prosigns for Morse code and the meanings of these special procedural signals in standard Morse code communications protocol.
International contests in code copying are still occasionally held. In July 1939 at a contest in Asheville, North Carolina in the United States Ted R. McElroy W1JYN set a still-standing record for Morse copying, 75.2 wpm.[34]Pierpont (2004) also notes that some operators may have passed 100 wpm.[34] By this time, they are "hearing" phrases and sentences rather than words. The fastest speed ever sent by a straight key was achieved in 1942 by Harry Turner W9YZE (d. 1992) who reached 35 wpm in a demonstration at a U.S. Army base. To accurately compare code copying speed records of different eras it is useful to keep in mind that different standard words (50 dit durations versus 60 dit durations) and different interword gaps (5 dit durations versus 7 dit durations) may have been used when determining such speed records. For example, speeds run with the codex standard word and the paris standard may differ by up to 20%.
Today among amateur operators there are several organizations that recognize high-speed code ability, one group consisting of those who can copy Morse at 60 wpm.[35] Also, Certificates of Code Proficiency are issued by several amateur radio societies, including the American Radio Relay League. Their basic award starts at 10 wpm with endorsements as high as 40 wpm, and are available to anyone who can copy the transmitted text. Members of the Boy Scouts of America may put a Morse interpreter's strip on their uniforms if they meet the standards for translating code at 5 wpm.

Through May 2013, the First, Second, and Third Class (commercial) Radiotelegraph Licenses using code tests based upon the codex standard word were still being issued in the United States by the Federal Communications Commission. The First Class license required 20 wpm code group and 25 wpm text code proficiency, the others 16 wpm code group test (five letter blocks sent as simulation of receiving encrypted text) and 20 wpm code text (plain language) test. It was also necessary to pass written tests on operating practice and electronics theory. A unique additional demand for the First Class was a requirement of a year of experience for operators of shipboard and coast stations using Morse. This allowed the holder to be chief operator on board a passenger ship. However, since 1999 the use of satellite and very high-frequency maritime communications systems (GMDSS) has made them obsolete. (By that point meeting experience requirement for the First was very difficult.)
Currently, only one class of license, the Radiotelegraph Operator License, is issued. This is granted either when the tests are passed or as the Second and First are renewed and become this lifetime license. For new applicants, it requires passing a written examination on electronic theory and radiotelegraphy practices, as well as 16 wpm code-group and 20 wpm text tests. However, the code exams are currently waived for holders of Amateur Extra Class licenses who obtained their operating privileges under the old 20 wpm test requirement.
International Morse code
Morse code has been in use for more than 160 years — longer than any other electrical coding system. What is called Morse code today is actually somewhat different from what was originally developed by Vail and Morse. The Modern International Morse code, or continental code, was created by Friedrich Clemens Gerke in 1848 and initially used for telegraphy between Hamburg and Cuxhaven in Germany. Gerke changed nearly half of the alphabet and all of the numerals, providing the foundation for the modern form of the code. After some minor changes, International Morse Code was standardized at the International Telegraphy Congress in 1865 in Paris and was later made the standard by the International Telecommunication Union (ITU). Morse's original code specification, largely limited to use in the United States and Canada, became known as American Morse code or "railroad code". American Morse code is now seldom used except in historical re-enactments.
Aviation

In aviation, pilots use radio navigation aids. To ensure that the stations the pilots are using are serviceable, the stations transmit a set of identification letters (usually a two-to-five-letter version of the station name) in Morse code. Station identification letters are shown on air navigation charts. For example, the VOR-DME based at Vilo Acuña Airport in Cayo Largo del Sur, Cuba is coded as "UCL", and UCL in Morse code is transmitted on its radio frequency. In some countries, during periods of maintenance, the facility may radiate a T-E-S-T code ( ▄▄▄ ▄ ▄ ▄ ▄ ▄▄▄ ) or the code may be removed which tells pilots and navigators that the station is unreliable. In Canada, the identification is removed entirely to signify the navigation aid is not to be used.[36][37] In the aviation service, Morse is typically sent at a very slow speed of about 5 words per minute. In the U.S., pilots do not actually have to know Morse to identify the transmitter because the dot/dash sequence is written out next to the transmitter's symbol on aeronautical charts. Some modern navigation receivers automatically translate the code into displayed letters.
Amateur radio

International Morse code today is most popular among amateur radio operators, in the mode commonly referred to as "continuous wave" or "CW". (This name was chosen to distinguish it from the damped wave emissions from spark transmitters, not because the transmission is continuous.) Other keying methods are available in radio telegraphy, such as frequency-shift keying.
The original amateur radio operators used Morse code exclusively since voice-capable radio transmitters did not become commonly available until around 1920. Until 2003, the International Telecommunication Union mandated Morse code proficiency as part of the amateur radio licensing procedure worldwide. However, the World Radiocommunication Conference of 2003 made the Morse code requirement for amateur radio licensing optional.[39] Many countries subsequently removed the Morse requirement from their licence requirements.[40]
Until 1991, a demonstration of the ability to send and receive Morse code at a minimum of five words per minute (wpm) was required to receive an amateur radio license for use in the United States from the Federal Communications Commission. Demonstration of this ability was still required for the privilege to use the HF bands. Until 2000, proficiency at the 20 wpm level was required to receive the highest level of amateur license (Amateur Extra Class); effective April 15, 2000, the FCC reduced the Extra Class requirement to 5 wpm.[41] Finally, effective on February 23, 2007, the FCC eliminated the Morse code proficiency requirements from all amateur radio licenses.
While voice and data transmissions are limited to specific amateur radio bands under U.S. rules, Morse code is permitted on all amateur bands — LF, MF, HF, VHF, and UHF. In some countries, certain portions of the amateur radio bands are reserved for transmission of Morse code signals only.
Because Morse code transmissions employ an on-off keyed radio signal, it requires less complex transmission equipment than other forms of radio communication. Morse code also requires less signal bandwidth than voice communication, typically 100–150 Hz, compared to the roughly 2,400 Hz used by single-sideband voice, although at a slower data rate.
Morse code is usually received as a high-pitched audio tone, so transmissions are easier to copy than voice through the noise on congested frequencies, and it can be used in very high noise / low signal environments. The fact that the transmitted power is concentrated into a very limited bandwidth makes it possible to use narrow receiver filters, which suppress or eliminate interference on nearby frequencies. The narrow signal bandwidth also takes advantage of the natural aural selectivity of the human brain, further enhancing weak signal readability.[citation needed] This efficiency makes CW extremely useful for DX (distance) transmissions, as well as for low-power transmissions (commonly called "QRP operation", from the Q-code for "reduce power"). There are several amateur clubs that require solid high speed copy, the highest of these has a standard of 60 wpm. The American Radio Relay League offers a code proficiency certification program that starts at 10 wpm.
The relatively limited speed at which Morse code can be sent led to the development of an extensive number of abbreviations to speed communication. These include prosigns, Q codes, and a set of Morse code abbreviations for typical message components. For example, cq is broadcast to be interpreted as "seek you" (I'd like to converse with anyone who can hear my signal). om (old man), yl (young lady) and xyl ("ex-young lady" – wife) are common abbreviations. yl or om is used by an operator when referring to the other operator, xyl or om is used by an operator when referring to his or her spouse. qthis "transmitting location" (spoken "my Q.T.H." is "my location"). The use of abbreviations for common terms permits conversation even when the operators speak different languages.
Although the traditional telegraph key (straight key) is still used by some amateurs, the use of mechanical semi-automatic keyers (known as "bugs") and of fully automatic electronic keyers is prevalent today. Software is also frequently employed to produce and decode Morse code radio signals. The ARRL has a readability standard for robot encoders called ARRL Farnsworth spacing[42] that is supposed to have higher readability for both robot and human decoders. Some programs like WinMorse[43] have implemented the standard.
Other uses
Radio navigation aids such as VORs and NDBs for aeronautical use broadcast identifying information in the form of Morse Code, though many VORstations now also provide voice identification.[44] Warships, including those of the U.S. Navy, have long used signal lamps to exchange messages in Morse code. Modern use continues, in part, as a way to communicate while maintaining radio silence.
Automatic Transmitter Identification System (ATIS) uses Morse code to identify uplink sources of analog satellite transmissions.
Many amateur radio repeaters identify with Morse, even though they are used for voice communications.
Applications for the general public

An important application is signalling for help through SOS, " ▄ ▄ ▄ ▄▄▄ ▄▄▄ ▄▄▄ ▄ ▄ ▄ ". This can be sent many ways: keying a radio on and off, flashing a mirror, toggling a flashlight, and similar methods. The SOS signal is not sent as three separate characters; rather, it is a prosign sos, and is keyed without gaps between characters.[45]
Some Nokia mobile phones offer an option to alert the user of an incoming text message with the Morse tone " ▄ ▄ ▄ ▄▄▄ ▄▄▄ ▄ ▄ ▄ " (representing SMS or Short Message Service).[46] In addition, applications are now available for mobile phones that enable short messages to be input in Morse Code.[47]
Morse code as an assistive technology
Morse code has been employed as an assistive technology, helping people with a variety of disabilities to communicate.[48][49][50][51] For example, the Android operating system versions 5.0 and higher allow users to input text using Morse Code as an alternative to a keypad or handwriting recognition.[52]
Morse can be sent by persons with severe motion disabilities, as long as they have some minimal motor control. An original solution to the problem that caretakers have to learn to decode has been an electronic typewriter with the codes written on the keys. Codes were sung by users; see the voice typewriter employing Morse or votem.[53]
Morse code can also be translated by computer and used in a speaking communication aid. In some cases, this means alternately blowing into and sucking on a plastic tube ("sip-and-puff" interface). An important advantage of Morse code over row column scanning is that once learned, it does not require looking at a display. Also, it appears faster than scanning.
In one case reported in the radio amateur magazine QST,[54] an old shipboard radio operator who had a stroke and lost the ability to speak or write could communicate with his physician (a radio amateur) by blinking his eyes in Morse. Two examples of communication in intensive care units were also published in QST magazine.[55][56] Another example occurred in 1966 when prisoner of war Jeremiah Denton, brought on television by his North Vietnamese captors, Morse-blinked the word torture. In these two cases, interpreters were available to understand those series of eye-blinks.
Representation, timing, and speeds
International Morse code is composed of five elements:[1]: §3
- short mark, dot or dit ( ▄ ): "dit duration" is one time unit long
- long mark, dash or dah ( ▄▄▄ ): three time units long
- inter-element gap between the dits and dahs within a character: one dot duration or one unit long
- short gap (between letters): three time units long
- medium gap (between words): seven time units long (formerly five[6])
Transmission
Morse code can be transmitted in a number of ways: Originally as electrical pulses along a telegraphwire, but later extended to an audio tone, a radio signal with short and long tones, or high and low tones, or as a mechanical, audible, or visual signal (e.g. a flashing light) using devices like an Aldis lamp or a heliograph, a common flashlight, or even a car horn. Some mine rescues have used pulling on a rope - a short pull for a dot and a long pull for a dah.
Morse code is transmitted using just two states (on and off). Morse code may be represented as a binary code, and that is what telegraph operators do when transmitting messages. Working from the above ITU definition and further defining a bit as a dot time, a Morse code sequence may be made from a combination of the following five bit-strings:
- short mark, dot or dit ( ▄ ): 1
- longer mark, dash or dah ( ▄▄▄ ): 111
- intra-character gap (between the dits and dahs within a character): 0
- short gap (between letters): 000
- medium gap (between words): 0000000
Note that the marks and gaps alternate: Dits and dahs are always separated by one of the gaps, and that the gaps are always separated by a dit or a dah.
Morse messages are generally transmitted by a hand-operated device such as a telegraph key, so there are variations introduced by the skill of the sender and receiver — more experienced operators can send and receive at faster speeds. In addition, individual operators differ slightly, for example, using slightly longer or shorter dahs or gaps, perhaps only for particular characters. This is called their "fist", and experienced operators can recognize specific individuals by it alone. A good operator who sends clearly and is easy to copy is said to have a "good fist". A "poor fist" is a characteristic of sloppy or hard to copy Morse code.
Cable code
The very long time constants of 19th and early 20th century submarine communications cables required a different form of Morse signalling. Instead of keying a voltage on and off for varying times, the dits and dahs were represented by two polarities of voltage impressed on the cable, for a uniform time.[57]
Timing
Below is an illustration of timing conventions. The phrase morse code, in Morse code format, would normally be written something like this, where –represents dahs and · represents dits:
Next is the exact conventional timing for this phrase, with ▓ representing "signal on", and ˽ representing "signal off", each for the time length of exactly one dit:
Spoken representation
Morse code is often spoken or written with dah for dashes, dit for dots located at the end of a character, and di for dots located at the beginning or internally within the character. Thus, the following Morse code sequence:
is spoken (or sung):
For use on radio, there is little point in learning to read written Morse as above; rather, the sounds of all of the letters and symbols need to be learned, for both sending and receiving.
Speed in words per minute
All Morse code elements depend on the dot / dit length. A dah is the length of 3 dits (with no gaps between), and spacings are specified in number of ditlengths. An unambiguous method of specifying the transmission speed is to specify the dit duration as, for example, 50 milliseconds.
Specifying the dit duration is, however, not the common practice. Usually, speeds are stated in words per minute. That introduces ambiguity because words have different numbers of characters, and characters have different dit lengths. It is not immediately clear how a specific word rate determines the dit duration in milliseconds.
Some method to standardize the transformation of a word rate to a dit duration is useful. A simple way to do this is to choose a dit duration that would send a typical word the desired number of times in one minute. If, for example, the operator wanted a character speed of 13 words per minute, the operator would choose a dit rate that would send the typical word 13 times in exactly one minute.
The typical word thus determines the dit length. It is common to assume that a word is 5 characters long. There are two common typical words: paris and codex. paris mimics a word rate that is typical of natural language words and reflects the benefits of Morse code's shorter code durations for common characters such as e and t. codex offers a word rate that is typical of 5 letter code groups (sequences of random letters). Using the word paris as a standard, the number of dit units is 50 and a simple calculation shows that the dit length at 20 words per minute is 60 milliseconds. Using the word codexwith 60 dit units, the dit length at 20 words per minute is 50 milliseconds.
Because Morse code is usually sent by hand, it is unlikely that an operator could be that precise with the dit length, and the individual characteristics and preferences of the operators usually override the standards.
For commercial radiotelegraph licenses in the United States, the Federal Communications Commission specifies tests for Morse code proficiency in words per minute and in code groups per minute.[58]: §13.207(c), §13.209(d) The FCC specifies that a "word" is 5 characters long. The Commission specifies Morse code test elements at 16 code groups per minute, 20 words per minute, 20 code groups per minute, and 25 words per minute.[58]: §13.203(b) The word per minute rate would be close to the paris standard, and the code groups per minute would be close to the codex standard.
While the Federal Communications Commission no longer requires Morse code for amateur radio licenses, the old requirements were similar to the requirements for commercial radiotelegraph licenses.[58]: §97.503, 1996
A difference between amateur radio licenses and commercial radiotelegraph licenses is that commercial operators must be able to receive code groups of random characters along with plain language text. For each class of license, the code group speed requirement is slower than the plain language text requirement. For example, for the Radiotelegraph Operator License, the examinee must pass a 20 word per minute plain text test and a 16 word per minute code group test.[31]
Based upon a 50 dit duration standard word such as paris, the time for one dit duration or one unit can be computed by the formula:
where: T is the unit time, or dit duration in milliseconds, and W is the speed in wpm.
High-speed telegraphy contests are held; according to the Guinness Book of Records in June 2005 at the International Amateur Radio Union's 6th World Championship in High Speed Telegraphy in Primorsko, Bulgaria, Andrei Bindasov of Belarus transmitted 230 Morse code marks of mixed text in one minute.[59]
Farnsworth speed
Sometimes, especially while teaching Morse code, the timing rules above are changed so two different speeds are used: A character speed and a text speed. The character speed is how fast each individual letter is sent. The text speed is how fast the entire message is sent. For example, individual characters may be sent at a 13 words-per-minute rate, but the intercharacter and interword gaps may be lengthened so the word rate is only 5 words per minute.
Using different character and text speeds is, in fact, a common practice, and is used in the Farnsworth method of learning Morse code.
Alternative display of common characters in International Morse code
Some methods of teaching Morse code use a dichotomic search table.
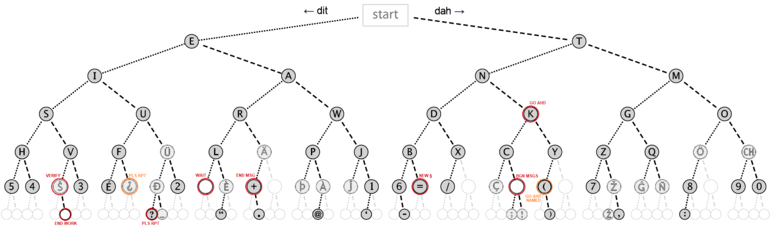
Learning methods
People learning Morse code using the Farnsworth method are taught to send and receive letters and other symbols at their full target speed, that is with normal relative timing of the dits, dahs, and spaces within each symbol for that speed. The Farnsworth method is named for Donald R. "Russ" Farnsworth, also known by his call sign, W6TTB. However, initially exaggerated spaces between symbols and words are used, to give "thinking time" to make the sound "shape" of the letters and symbols easier to learn. The spacing can then be reduced with practice and familiarity.
Another popular teaching method is the Koch method, invented in 1935 by the German engineer and former stormtrooper Ludwig Koch,[60] which uses the full target speed from the outset but begins with just two characters. Once strings containing those two characters can be copied with 90% accuracy, an additional character is added, and so on until the full character set is mastered.
In North America, many thousands of individuals have increased their code recognition speed (after initial memorization of the characters) by listening to the regularly scheduled code practice transmissions broadcast by W1AW, the American Radio Relay League's headquarters station.[61] As of 2015, the United States military taught Morse code as an 81-day self-paced course, having phased out more traditional classes.[62]
Mnemonics

Visual mnemonic charts have been devised over the ages. Baden-Powell included one in the Girl Guideshandbook[63] in 1918.
In the United Kingdom, many people learned the Morse code by means of a series of words or phrases that have the same rhythm as a Morse character. For instance, q in Morse is dah dah di dah , which can be memorized by the phrase "God Save the Queen", and the Morse for f is di di dah dit , which can be memorized as "Did she like it?"[d]
Letters, numbers, punctuation, prosigns for Morse code and non-Latin variants
| Category | Character | Code |
|---|---|---|
| Letters | A, a | |
| Letters | B, b | |
| Letters | C, c | |
| Letters | D, d | |
| Letters | E, e | |
| Letters | F, f | |
| Letters | G, g | |
| Letters | H, h | |
| Letters | I, i | |
| Letters | J, j | |
| Letters | K, k Prosign for general invitation to transmit | |
| Letters | L, l | |
| Letters | M, m | |
| Letters | N, n | |
| Letters | O, o | |
| Letters | P, p | |
| Letters | Q, q | |
| Letters | R, r | |
| Letters | S, s | |
| Letters | T, t | |
| Letters | U, u | |
| Letters | V, v | |
| Letters | W, w | |
| Letters | X, x | |
| Letters | Y, y | |
| Letters | Z, z | |
| Numbers | 0 | |
| Numbers | 1 | |
| Numbers | 2 | |
| Numbers | 3 | |
| Numbers | 4 | |
| Numbers | 5 | |
| Numbers | 6 | |
| Numbers | 7 | |
| Numbers | 8 | |
| Numbers | 9 | |
| Punctuation | Period [.] | |
| Punctuation | Comma [,] | |
| Punctuation | Question mark [?] | |
| Punctuation | Apostrophe ['] | |
| Nonstandard punctuation[e] | Exclamation point [!][e] kw digraph | |
| Punctuation | Slash or Fraction bar [/] dn digraph | |
| Punctuation | Open parenthesis [(] kn digraph Unofficial prosign for exclusive invitation to transmit | |
| Punctuation | Close parenthesis [)] | |
| Nonstandard punctuation[e] | Ampersand [&][e] as digraph Prosign for wait | |
| Punctuation | Colon [:] | |
| Nonstandard punctuation[e] | Semicolon [;] [e] | |
| Punctuation | Double dash [=] bt digraph Prosign for new section or new paragraph | |
| Punctuation | Plus sign [+] rn digraph Prosign for new message or new page | |
| Punctuation | Hyphen or Minus sign [-] | |
| Nonstandard punctuation[e] | Underscore [ _ ][e] | |
| Punctuation | Quotation mark ["] | |
| Nonstandard punctuation[e] | Dollar sign [$][e] sx digraph[e] | |
| Punctuation | At sign [@] ac digraph | |
| Prosigns | End of work sk digraph | |
| Prosigns | Error hh digraph | |
| Prosigns | General invitation to transmit Also used for letter K | |
| Prosigns | Starting signal ct digraph | |
| Prosigns | New message follows rn digraph Message or page separator[f] | |
| Prosigns | Verified Also used for letter Ŝ | |
| Prosigns | Wait Proposed for use as ampersand [&] | |
| non-Latin[e] extensions | À, à Code shared with Å | |
| non-Latin[e] extensions | Ä, ä Code shared with Æ, Ą | |
| non-Latin[e] extensions | Å, å Code shared with À | |
| non-Latin[e] extensions | Ą, ą Code shared with Ä, Æ | |
| non-Latin[e] extensions | Æ, æ Code shared with Ä, Ą | |
| non-Latin[e] extensions | Ć, ć Code shared with Ĉ, Ç | |
| non-Latin[e] extensions | Ĉ, ĉ Code shared with Ć, ç | |
| non-Latin[e] extensions | Ç, ç Code shared with Ć, Ĉ | |
| non-Latin[e] extensions | CH, ch Code shared with Ĥ, Š | |
| non-Latin[e] extensions | Đ, đ Code shared with É,[g] Ę Distinct from eth (Ð, ð) | |
| non-Latin[e] extensions | Ð, ð Distinct from D with stroke (Đ, đ) | |
| non-Latin extensions | É, é[g] Code shared with Đ, Ę | |
| non-Latin[e] extensions | È, è Code shared with Ł | |
| non-Latin[e] extensions | Ę, ę Code shared with Đ, É,[g] | |
| non-Latin[e] extensions | Ĝ, ĝ | |
| non-Latin[e] extensions | Ĥ, ĥ Code shared with CH, Š | |
| non-Latin[e] extensions | Ĵ, ĵ | |
| non-Latin[e] extensions | Ł, ł Code shared with È | |
| non-Latin[e] extensions | Ń, ń Code shared with Ñ | |
| non-Latin[e] extensions | Ñ, ñ Code shared with Ń | |
| non-Latin[e] extensions | Ó, ó Code shared with Ö, Ø | |
| non-Latin[e] extensions | Ö, ö Code shared with Ó, Ø | |
| non-Latin[e] extensions | Ø, ø Code shared with Ó, Ö | |
| non-Latin[e] extensions | Ś, ś | |
| non-Latin[e] extensions | Ŝ, ŝ Prosign for verified | |
| non-Latin[e] extensions | Š, š Code shared with CH, Ĥ | |
| non-Latin[e] extensions | Þ, þ | |
| non-Latin[e] extensions | Ü, ü Code shared with Ŭ | |
| non-Latin[e] extensions | Ŭ, ŭ Code shared with Ü | |
| non-Latin[e] extensions | Ź, ź | |
| non-Latin[e] extensions | Ż, ż |
Prosigns
Prosigns for Morse code are special (usually) unwritten procedural signals or symbols that are used to indicate changes in communications protocol status or white space text formatting actions.
Symbol representations
The symbols [!], [$], and [&] are not defined inside the official ITU-R International Morse Code Recommendation,[1] but informal conventions for them exist. (The [@] symbol was formally added in 2004.)
- Exclamation mark
- There is no standard representation for the exclamation mark [!], although the kw digraph ( ▄▄▄ ▄ ▄▄▄ ▄ ▄▄▄ ▄▄▄ ) was proposed in the 1980s by the HeathkitCompany.[h] While Morse code translation software prefers the Heathkit version, on-air use is not yet universal as some amateur radio operators in North America and the Caribbean continue to use the older mn digraph ( ▄▄▄ ▄▄▄ ▄▄▄ ▄ )[i] copied over from American Morse landline code.
- Currency symbols
- The ITU has never formally codified any currency symbols into Morse code: The unambiguous ISO 4217 currency codes are preferred for transmission.
- The [$] sign code was represented in the Phillips Code[j] as two characters "sx", which became merged into sx ( ▄ ▄ ▄ ▄▄▄ ▄ ▄ ▄▄▄ ).
- Ampersand [&]
- The suggested unofficial encoding of the ampersand [&] sign listed above, often shown as as, is also the official Morse prosign for wait. In addition, the American Morse encoding for an ampersand ( ▄ ▄ ▄ ▄ ) was similar to es ( ▄ ▄ ▄ ▄ ) and hams have nearly universally carried over this use as an abbreviation for "and" (e.g. wx hr cold es rainy the weather here is cold and rainy).
- Keyboard "at" sign [@]
- On 24 May 2004 – the 160th anniversary of the first public Morse telegraph transmission – the Radiocommunication Bureau of the International Telecommunication Union (ITU-R) formally added the [@] ("commercial at" or "commat") character to the official Morse character set, using the sequence denoted by the ac digraph: ▄ ▄▄▄ ▄▄▄ ▄ ▄▄▄ ▄ .[1][67]
- This sequence was reported to have been chosen to represent "A[t] C[ommercial]", or a letter "a" inside a swirl represented by a letter "C". The new character facilitates sending e‑mail addresses by Morse code, and is notable since it is the first official addition to the Morse set of characters since World War I.[67]
Diacritics and non-Latin extensions
The typical tactic for creating Morse codes for diacritics and non-Latin alphabetic scripts has been to begin by simply using the International Morse codes used for letters whose sound matches the sound of the local alphabet. Because Gerke code (the predecessor to International Morse) was in official use in central Europe,[23] and included four characters not included in the International Morse standard (ä, ö, ü, and ch) it has served as a beginning-point for other languages that use an alphabetic script, but require codes for letters not accommodated by International Morse.
The usual method has been to first transliterate the sounds represented by the International code and the four unique Gerke codes into the local alphabet, hence Greek, Hebrew, Russian, and Ukrainian Morse codes. If more codes are needed, one can either invent a new code or convert an otherwise unused code from either code set to the non-Latin letter. For example:
- ñ in Spanish Morse is ▄▄▄ ▄▄▄ ▄ ▄▄▄ ▄▄▄ , a language-specific code not used in either International or Gerke Morse.
- For the Greek letter Ψ, Greek Morse code uses the International Morse code for q, ▄▄▄ ▄▄▄ ▄ ▄▄▄ , which has no corresponding letter in modern Greek; note that Ψ and Q have no historical, phonetic, or shape relationship.
For Russian and Bulgarian, Russian Morse code is used to map the Cyrillic characters to four-element codes. Many of the characters are encoded the same as their latin-alphabet look-alikes or sound-alikes (a, o, e, i, t, m, n, r, k, etc.). The Bulgarian alphabet contains 30 characters, which exactly match all possible combinations of 1, 2, 3, and 4 dits and dahs (Russian ы is used as Bulgarian ь, Russian ь is used as Bulgarian ъ). Russian requires two more codes, for letters э and ъ which are each encoded with 5 elements.
Non-alphabetic scripts require more radical adaption. Japanese Morse code (Wabun code) has a separate encoding for kana script; although many of the codes are used for International Morse, the sounds they represent are mostly unrelated. The Japanese / Wabun code includes special prosigns for switching back-and-forth from International Morse: ▄▄▄ ▄ ▄ ▄▄▄ ▄▄▄ ▄▄▄ signals a switch from International Morse to Wabun, and ▄ ▄ ▄ ▄▄▄ ▄ to return from Wabun to International Morse.
For Chinese, Chinese telegraph code is used to map Chinese characters to four-digit codes and send these digits out using standard Morse code. Korean Morse code[68] uses the SKATS mapping, originally developed to allow Korean to be typed on western typewriters. SKATS maps hangul characters to arbitrary letters of the Latin script and has no relationship to pronunciation in Korean.
Unusual variants
During early World War I (1914–1916), Germany briefly experimented with 'dotty' and 'dashy' Morse, in essence adding a dot or a dash at the end of each Morse symbol. Each one was quickly broken by Allied SIGINT, and standard Morse was restored by Spring 1916. Only a small percentage of Western Front (North Atlantic and Mediterranean Sea) traffic was in 'dotty' or 'dashy' Morse during the entire war. In popular culture, this is mostly remembered in the book The Codebreakers by Kahn and in the national archives of the UK and Australia (whose SIGINT operators copied most of this Morse variant). Kahn's cited sources come from the popular press and wireless magazines of the time.[69]
Other forms of Fractional Morse or Fractionated Morse have emerged.[70]
Decoding software
Decoding software for Morse code ranges from software-defined wide-band radio receivers, coupled to the Reverse Beacon Network,[71] which decodes signals and detects cq messages on ham bands, to smartphone applications.[72]
See also
Footnotes
- ^ Until 1949, words were separated by a space equal to five dits.[6]
- ^ The time needed to transmit the word paris is typically used as the standard "word" for calculating the "word per minute" rate. Other standard "words" such as comex are also used.[7]
- ^ These modern keys are operated by one or two "paddles" pressed left and right, instead of pressing down a lever, as in the traditional telegraph keys, pictured at the start of this article. Operating of paddle keys is similar to use of the old Vibroplex clockwork telegraph keys: Pressing the paddle to the left generates a series of repeated dahs until the paddle is released; pressing the paddle to the right produces a similar series of dits; and with two-paddle electronic keys, squeezing the two paddles from both sides produces an alternating dit dah dit dah sequence. (For left-handed operators, the actions are reversed.)
- ^ A well-known Morse code rhythm from the Second World War period derives from Beethoven's Fifth Symphony, the opening phrase of which was regularly played at the beginning of BBC broadcasts. The timing of the notes corresponds to the Morse for v, di di di dah ( ▄ ▄ ▄ ▄▄▄ ), understood as "'V' for Victory".[64][65]
- ^ a b c d e f g h i j k l m n o p q r s t u v w x y z aa ab ac ad ae af ag ah ai aj ak al am an ao
The character or symbol encoding is not in either ITU-R M.1172[66] or ITU-R M.1677-1 .[1] - ^ Single-line decoding display may use printed "+" for message separator prosign.
- ^ a b c Although not strictly a Latin alphabet character, the code for É is part of the ITU-R Morse code standard, and is the only accented character included in the recommendation.[1]
- ^ Heathkit was a popular, long-standing vendor of kits for amateur radio equipment.
- ^ mn or oe, ▄▄▄ ▄▄▄ ▄▄▄ ▄ , is shared with unofficial ö, ó, and ø used in some non-Latin alphabets.
- ^ The Phillips Code was a huge collection of abbreviations used on land line telegraphy.














![{\displaystyle {\begin{aligned}\varphi ^{n}&=\varphi ^{n-1}+\varphi ^{n-2},\\[3mu]\psi ^{n}&=\psi ^{n-1}+\psi ^{n-2}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/282a0b620cb2eca72787ef444e6d07d39678d383)

![{\displaystyle {\begin{aligned}U_{n}&=a\varphi ^{n}+b\psi ^{n}\\[3mu]&=a(\varphi ^{n-1}+\varphi ^{n-2})+b(\psi ^{n-1}+\psi ^{n-2})\\[3mu]&=a\varphi ^{n-1}+b\psi ^{n-1}+a\varphi ^{n-2}+b\psi ^{n-2}\\[3mu]&=U_{n-1}+U_{n-2}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49e155e3c74b9d82976473240c1fc8f5db5d0f1f)


![{\displaystyle {\begin{aligned}a&={\frac {U_{1}-U_{0}\psi }{\sqrt {5}}},\\[3mu]b&={\frac {U_{0}\varphi -U_{1}}{\sqrt {5}}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b7a1f5df3f3d8a6b6e48e76a19c75a2b5c65645)




















































![{\displaystyle {\begin{aligned}F_{2n-1}&={F_{n}}^{2}+{F_{n-1}}^{2}\\[5pt]F_{2n{\phantom {{}-1}}}&=(F_{n-1}+F_{n+1})F_{n}\\[5pt]&=(2F_{n-1}+F_{n})F_{n}\\[5pt]&=(2F_{n+1}-F_{n})F_{n}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64b95fd1ea97b7a4315e8ee4ddb7f6b44c7681f0)



































































































































No comments:
Post a Comment