Should the theorem of the hippopotamus prove true through the avenue of science and the anthropologist world than within this post it is the continuing work that will eventually prove in theory the formation of the Earth’s core and the make-up wherefrom.
First evolution and the
path from the ocean to land animals; importance of time and the traveling
biology into life form of new not complete.
As the gentle tack of evolution continues to explain our existence on
this planet it is imperative that the work of past evolutionists is put to
task. I am not filling in the blanks as
that would prove presumption, instead I have chosen to allow nature to take it’s
natural course and place reliance on the obvious.
To be of interest in
comprehension I know that each track that is found is exciting and full: The trees and branches!
Black rhinoceros
Jump to navigation
Jump to search
The black rhinoceros or hook-lipped rhinoceros (Diceros bicornis) is a species of rhinoceros, native to eastern and southern Africa including Angola, Botswana, Kenya, Malawi, Mozambique, Namibia, South Africa, Eswatini, Tanzania, Zambia, and Zimbabwe. Although the rhinoceros is referred to as black, its colours vary from brown to grey.
The other African rhinoceros is the white rhinoceros (Ceratotherium simum). The word "white" in the name "white rhinoceros" is often said to be a misinterpretation of the Afrikaans word wyd (Dutch wijd) meaning wide, referring to its square upper lip, as opposed to the pointed or hooked lip of the black rhinoceros. These species are now sometimes referred to as the square-lipped (for white) or hook-lipped (for black) rhinoceros.[5]
The species overall is classified as critically endangered (even though the south-western black rhinoceros is classified as near threatened). Three subspecies have been declared extinct, including the western black rhinoceros, which was declared extinct by the International Union for Conservation of Nature (IUCN) in 2011.[6][7]
The species was first named Rhinoceros bicornis by Carl Linnaeus in the 10th edition of his Systema naturae
in 1758. The name means "double-horned rhinoceros". There is some
confusion about what exactly Linnaeus conceived under this name as this
species was probably based upon the skull of a single-horned Indian rhinoceros (Rhinoceros unicornis), with a second horn artificially added by the collector. Such a skull is known to have existed and Linnaeus even mentioned India
as origin of this species. However he also referred to reports from
early travellers about a double-horned rhino in Africa and when it
emerged that there is only one, single-horned species of rhino in India,
Rhinoceros" bicornis was used to refer to the African rhinos (the white rhino only became recognised in 1812).[8] In 1911 this was formally fixed and the Cape of Good Hope officially declared the type locality of the species.[9]
| Black rhinoceros or hook-lipped rhinoceros[1] | |
|---|---|

| |
| Male at Cincinnati Zoo | |

| |
| Female at the Taronga Zoo | |
| Scientific classification | |
| Kingdom: | Animalia |
| Phylum: | Chordata |
| Class: | Mammalia |
| Order: | Perissodactyla |
| Family: | Rhinocerotidae |
| Genus: | Diceros Gray, 1821 |
| Species: |
D. bicornis
|
| Binomial name | |
| Diceros bicornis | |
| Subspecies | |
|
Diceros bicornis bicornis † Diceros bicornis brucii † Diceros bicornis chobiensis Diceros bicornis ladoensis Diceros bicornis longipes † Diceros bicornis michaeli Diceros bicornis minor Diceros bicornis occidentalis | |

| |
| Historical black rhinoceros range (ca. 1700 A.D.).[3] Hatched: Possible historical range in West Africa.[4] | |

| |
| Current black rhinoceros range Extant, resident Extinct Extant & Reintroduced (resident) Extant & Assisted Colonisation (resident) | |
| Synonyms | |
| |
The other African rhinoceros is the white rhinoceros (Ceratotherium simum). The word "white" in the name "white rhinoceros" is often said to be a misinterpretation of the Afrikaans word wyd (Dutch wijd) meaning wide, referring to its square upper lip, as opposed to the pointed or hooked lip of the black rhinoceros. These species are now sometimes referred to as the square-lipped (for white) or hook-lipped (for black) rhinoceros.[5]
The species overall is classified as critically endangered (even though the south-western black rhinoceros is classified as near threatened). Three subspecies have been declared extinct, including the western black rhinoceros, which was declared extinct by the International Union for Conservation of Nature (IUCN) in 2011.[6][7]
Taxonomy
Subspecies
The intraspecific variation in the black rhinoceros has been discussed by various authors and is not finally settled.[10] The most accepted scheme considers seven or eight subspecies,[3][11][12] of which three became extinct in historical times and one is on the brink of extinction:- Southern black rhinoceros or Cape black rhinoceros (D. b. bicornis) – Extinct. Once abundant from the Cape of Good Hope to Transvaal, South Africa and probably into the south of Namibia, this was the largest subspecies. It became extinct due to excessive hunting and habitat destruction around 1850.[13]
- North-eastern black rhinoceros (D. b. brucii) – Extinct. Formerly central Sudan, Eritrea, northern and southeastern Ethiopia, Djibouti and northern and southeastern Somalia. Primal populations in northern Somalia vanished during the early 20th century.
- Chobe black rhinoceros (D. b. chobiensis) – A local subspecies restricted to the Chobe Valley in southeastern Angola, Namibia (Zambezi Region) and northern Botswana. Nearly extinct, possibly only one surviving specimen in Botswana.[12]
- Uganda black rhinoceros (D. b. ladoensis) – Former distribution from South Sudan, across Uganda into western Kenya and southwesternmost Ethiopia. Black rhinos are considered extinct across most of this area and its conservational status is unclear. Probably surviving in Kenyan reserves.
- Western black rhinoceros (D. b. longipes) – Extinct. Once lived in South Sudan, northern Central African Republic, southern Chad, northern Cameroon, northeastern Nigeria and south-eastern Niger. The range possibly stretched west to the Niger River in western Niger, though this is unconfirmed. The evidence from Liberia and Burkina Faso mainly rests upon the existence of indigenous names for the rhinoceros.[4] A far greater former range in West Africa as proposed earlier[14] is doubted by a 2004 study.[4] The last known wild specimens lived in northern Cameroon. In 2006 an intensive survey across its putative range in Cameroon failed to locate any, leading to fears that it was extinct in the wild.[6][15] On 10 November 2011 the IUCN declared the western black rhinoceros extinct.[6]
- Eastern black rhinoceros (D. b. michaeli) – Had a historical distribution from South Sudan, Uganda, Ethiopia, down through Kenya into north-central Tanzania. Today, its range is limited primarily to Kenya and Tanzania.
- South-central black rhinoceros (D. b. minor) – Most widely distributed subspecies, characterised by a compact body, proportionally large head and prominent skin-folds. Ranged from north-eastern South Africa (KwaZulu-Natal) to northeastern Tanzania and southeastern Kenya. Preserved in reserves throughout most of its former range but probably extinct in eastern Angola, southern Democratic Republic of Congo and possibly Mozambique. Extinct but reintroduced in Malawi, Botswana, and Zambia.
- South-western black rhinoceros (D. b. occidentalis) – A small subspecies, adapted to survival in desert and semi-desert conditions. Originally distributed in north-western Namibia and southwestern Angola, today restricted to wildlife reserves in Namibia with sporadic sightings in Angola. These populations are often erroneously referred to D. b. bicornis or D. b. minor but represent a subspecies in their own right.[12]
Evolution
The rhinoceros originated in the Eocene about fifty million years ago alongside other members of Perissodactyla.[17] Ancestors of the black and the white rhinoceros were present in Africa by the end of the Late Miocene about ten million years ago.[17] The two species evolved from the common ancestral species Ceratotherium neumayri during this time. The clade comprising the genus Diceros is characterised by an increased adaptation to browsing. Between four and five million years ago, the black rhinoceros diverged from the white rhinoceros.[17] After this split, the direct ancestor of Diceros bicornis, Diceros praecox was present in the Pliocene of East Africa (Ethiopia, Kenya, Tanzania). D. bicornis evolved from this species during the Late Pliocene – Early Pleistocene.[18] With the oldest definitive record at the Pliocene-Pleistocene boundary c. 2.5 Ma at Koobi Fora, Kenya.[19]Description
Comparative illustration of black (top) and white rhinos (bottom)
The longest known black rhinoceros horn measured nearly 1.5 m (4.9 ft) in length.[22] Sometimes, a third, smaller horn may develop.[23] These horns are used for defense, intimidation, and digging up roots and breaking branches during feeding. The black rhino is smaller than the white rhino, and is close in size to the Javan rhino of Indonesia. It has a pointed and prehensile upper lip, which it uses to grasp leaves and twigs when feeding.[22] The white rhinoceros has square lips used for eating grass. The black rhinoceros can also be distinguished from the white rhinoceros by its size, smaller skull, and ears; and by the position of the head, which is held higher than the white rhinoceros, since the black rhinoceros is a browser and not a grazer. This key differentiation is further illustrated by the shape of the two species mouths (lips): the "square" lip of the white rhinoceros is an adaptation for grazing, and the "hooked" lip of the black rhinoceros is an adaptation to help browsing.[citation needed]
A black rhinoceros skull
Distribution
Prehistorical range
As with many other components of the African large mammal fauna, black rhinos probably had a wider range in the northern part of the continent in prehistoric times than today. However this seems to have not been as extensive as that of the white rhino. Unquestionable fossil remains have not yet been found in this area and the abundant petroglyphs found across the Sahara desert are often too schematic to unambiguously decide whether they depict black or white rhinos. Petroglyphs from the Eastern Desert of southeastern Egypt relatively convincingly show the occurrence of black rhinos in these areas in prehistoric times.[27]Historical and extant range
The natural range of the black rhino included most of southern and eastern Africa, but it did not occur in the Congo Basin, the tropical rainforest areas along the Bight of Benin, the Ethiopian Highlands, and the Horn of Africa.[3] Its former native occurrence in the extremely dry parts of the Kalahari desert of southwestern Botswana and northwestern South Africa is uncertain.[28] In western Africa it was abundant in an area stretching east to west from Eritrea and Sudan through South Sudan to southeastern Niger, and especially around Lake Chad. Its occurrence further to the west is questionable, though often purported to in literature.[4] Today it is totally restricted to protected nature reserves and has vanished from many countries in which it once thrived, especially in the west and north of its former range. The remaining populations are highly scattered. Some specimens have been relocated from their habitat to better protected locations, sometimes across national frontiers.[2] The black rhino has been successfully reintroduced to Malawi since 1993, where it became extinct in 1990.[29] Similarly it was reintroduced to Zambia (North Luangwa National Park) in 2008, where it had become extinct in 1998,[30] and to Botswana (extinct in 1992, reintroduced in 2003).[31]In May 2017, 18 Eastern Black Rhinos were translocated from South Africa to the Akagera National Park in Rwanda. The park had around 50 rhinos in the 1970s but the numbers dwindled to zero by 2007. In September 2017, the birth of a calf raised the population to 19. The park has dedicated rhino monitoring teams to protect the animals from poaching.[32][33]
In October 2017, The governments of Chad and South Africa reached an agreement to transfer six black rhinos from South Africa to Zakouma National Park in Chad. Once established, this will be the northernmost population of the species. The species was wiped out from Chad in the 1970s and is under severe pressure from poaching in South Africa. The agreement calls for South African experts to assess the habitat, local management capabilities, security and the infrastructure before the transfer can take place.[34]
Behavior
An adult black rhinoceros with young grazing in Krefeld Zoo
Black rhino at Moringa waterhole, Etosha National Park
Black rhinoceros in captivity and reservations sleep patterns have been recently studied to show that males sleep longer on average than females by nearly double the time. Other factors that play a role in their sleeping patterns is the location of where they decide to sleep. Although they do not sleep any longer in captivity, they do sleep at different times due to their location in captivity, or section of the park.[38]
The black rhino has a reputation for being extremely aggressive, and charges readily at perceived threats. They have even been observed to charge tree trunks and termite mounds.[citation needed] Black rhinos will fight each other, and they have the highest rates of mortal combat recorded for any mammal: about 50% of males and 30% of females die from combat-related injuries.[39] Adult rhinos normally have no natural predators, thanks to their imposing size as well as their thick skin and deadly horns.[40] However, adult black rhinos have fallen prey to crocodiles in exceptional circumstances.[41] Calves and, very seldom, small sub-adults may be preyed upon by lions as well.[3]
Black rhinoceros follow the same trails that elephants use to get from foraging areas to water holes. They also use smaller trails when they are browsing. They are very fast and can get up to speeds of 55 kilometres per hour (34 mph) running on their toes.[42][43]
Diet
Chewing on plants
There is some variance in the exact chemical composition of rhinoceros horns. This variation is directly linked to diet and can be used as a means of rhino identification. Horn composition has helped scientists pinpoint the original location of individual rhinos, allowing for law enforcement to more accurately and more frequently identify and penalize poachers.[51]
Communication
The black rhino has powerful tube-shaped ears that can freely rotate in all directions. This highly developed sense of hearing allows black rhinos to detect sound over vast distances.[53]
Reproduction
Mother and calf in Lewa, central Kenya
When in season the females will mark dung piles. Males will follow females when they are in season; when she defecates he will scrape and spread the dung, making it more difficult for rival adult males to pick up her scent trail.
Courtship behaviors before mating include snorting and sparring with the horns among males. Another courtship behavior is called bluff and bluster, where the rhino will snort and swing its head from side to side aggressively before running away repeatedly. Breeding pairs stay together for 2–3 days and sometimes even weeks. They mate several times a day over this time and copulation lasts for a half-hour.
The gestation period for a black rhino is 15 months. The single calf weighs about 35–50 kilograms (80–110 lb) at birth, and can follow its mother around after just three days. Weaning occurs at around 2 years of age for the offspring. The mother and calf stay together for 2–3 years until the next calf is born; female calves may stay longer, forming small groups. The young are occasionally taken by hyenas and lions. Sexual maturity is reached from 5 to 7 years old for females, and 7 to 8 years for males. The life expectancy in natural conditions (without poaching pressure) is from 35 to 50 years.[54]
Conservation
Black rhino in the Maasai Mara
In 1992, nine rhinos were brought from Chete National Park, Zimbabwe to Australia via Cocos Island. After the natural deaths of the males in the group, four males were brought in from United States and have since adapted well to captivity and new climate.[59] Calves and some subadults are preyed on by lions, but predation is rarely taken into account in managing the black rhinoceros.[citation needed] This is a major flaw because predation should be considered when attributing cause to the poor performance of the black rhinoceros population.[60] In 2002 only ten western black rhinos remained in Cameroon, and in 2006 intensive surveys across its putative range failed to locate any, leading to fears that this subspecies had become extinct.[15] In 2011 the IUCN declared the western black rhino extinct.[61] There was a conservation effort in which black rhinos were translocated, but their population did not improve, as they did not like to be in an unfamiliar habitat.
Under CITES Appendix I all international commercial trade of the black rhino horn is prohibited since 1977.[37] China though having joined CITES since 8 April 1981 is the largest importer of black rhino horns.[62][citation needed] However, this is a trade in which not only do the actors benefit, but so do the nation states ignoring them as well. Nonetheless, people continue to remove the rhino from its natural environment and allow for a dependence on human beings to save them from endangerment.[63] Parks and reserves have been made for protecting the rhinos with armed guards keeping watch, but even still many poachers get through and harm the rhinos for their horns. Many have considered extracting rhino horns in order to deter poachers from slaughtering these animals or potentially bringing them to other breeding grounds such as the US and Australia.[63] This method of extracting the horn, known as dehorning, consists of tranquilizing the rhino then sawing the horn almost completely off to decrease initiative for poaching, although the effectiveness of this in reducing poaching is not known and rhino mothers are known to use their horns to fend off predators.[64]
The only rhino subspecies that has recovered somewhat from the brink of extinction is the southern white rhinoceros, whose numbers now are estimated around 14,500, up from fewer than 50 in the first decade of the 20th century.[65] But there seems to be hope for the black rhinoceros in recovering their gametes from dead rhinos in captivity. This shows promising results for producing black rhinoceros embryos, which can be used for testing sperm in vitro.[66]
A January 2014 auction for a permit to hunt a black rhinoceros in Namibia sold for $350,000 at a fundraiser hosted by the Dallas Safari Club. The auction drew considerable criticism as well as death threats directed towards members of the club and the man who purchased the permit.[67] This permit was issued for 1 of 18 black rhinoceros specifically identified by Namibia's Ministry of Environment and Tourism as being past breeding age and considered a threat to younger rhinos. The $350,000 that the hunter paid for the permit was used by the Namibian government to fund anti-poaching efforts in the country.[68]
Threats
Today, there are various threats posed to the black rhinoceros including habitat changes, illegal poaching, and competing species. Civil disturbances, such as war, have made mentionably negative effects on the black rhinoceros populations in since the 1960s in countries including, but not limited to, Chad, Cameroon, Rwanda, Mozambique, and Somalia.[2] In the Addo Elephant National Park in South Africa, the African elephant Loxodonta africana is posing slight concern involving the black rhinoceroses who also inhabit the area. Both animals are browsers; however, the elephant's diet consists of a wider variety of foraging capacity, while the rhinoceros primarily sticks to dwarf shrubs. The black rhinoceros has been found to eat grass as well; however, the shortening of its range of available food could be potentially problematic.[69]Black rhinoceros face problems associated with the minerals they ingest. They have become adjusted to ingesting less iron in the wild due to their evolutionary progression, which poses a problem when placed in captivity. These rhinoceroses can overload on iron, which leads to build up in the lungs, liver, spleen and small intestine.[70] Not only do these rhinoceros face threats being in the wild, but in captivity too. Black rhinoceros have become more susceptible to disease in captivity with high rates of mortality.[66]
Illegal poaching for the international rhino horn trade is the main and most detrimental threat.[2] The killing of these animals is not unique to modern-day society. The Chinese have maintained reliable documents of these happenings dating back to 1200 B.C.[71] The ancient Chinese often hunted rhino horn for the making of wine cups, as well as the rhino's skin to manufacture imperial crowns, belts and armor for soldiers.[71] A major market for rhino horn has historically been in the Middle East nations to make ornately carved handles for ceremonial daggers called jambiyas. Demand for these exploded in the 1970s, causing the black rhinoceros population to decline 96% between 1970 and 1992. The horn is also used in traditional Chinese medicine, and is said by herbalists to be able to revive comatose patients, facilitate exorcisms and various methods of detoxification,[71] cure fevers, and aid male sexual stamina and fertility.[72] It is also hunted for the superstitious belief that the horns allow direct access to Heaven due to their unique location and hollow nature.[71] The purported effectiveness of the use of rhino horn in treating any illness has not been confirmed, or even suggested, by medical science. In June 2007, the first-ever documented case of the medicinal sale of black rhino horn in the United States (confirmed by genetic testing of the confiscated horn) occurred at a traditional Chinese medicine supply store in Portland, Oregon's Chinatown.[72]
References
- Patte, David (26 June 2007). "Portland Man Pleads Guilty to Selling Black Rhino Horn". U.S. Fish & Wildlife Service. Archived from the original on 8 August 2007. Retrieved 29 June 2007.
Further reading
- Emslie, R. & Brooks, M. (1999). African Rhino. Status Survey and Conservation Action Plan. IUCN/SSC African Rhino Specialist Group. IUCN, Gland, Switzerland and Cambridge, UK. ISBN 2-8317-0502-9.
- Rookmaaker, L. C. (2005). "Review of the European perception of the African rhinoceros". Journal of Zoology. 265 (4): 365–376. doi:10.1017/S0952836905006436. S2CID 86237288.
External links
| Wikispecies has information related to Diceros bicornis |
| Wikimedia Commons has media related to Diceros bicornis. |
- Black rhinoceros at Curlie
- Black Rhino Info & Black Rhino Pictures on the Rhino Resource Center website.
- "Black Rhinoceros" (PDF). Zoological Parks Board of New South Wales. Archived from the original (PDF) on 28 September 2007. Retrieved 9 October 2007.
- www.savetherhino.org
- WildLifeNow Website for the Tony Fitzjohn/George Adamson African Wildlife Preservation Trust, supporting the Mkomazi Game Reserve and Mkomazi Rhino Sanctuary in Tanzania
- U.S. Fish & Wildlife Service Species Profile
- Sebakwe Black Rhino Trust dedicated to black rhino conservation in Zimbabwe
- A Radiolab interview with the man that won the auction to hunt a black rhino
Categories:
- IUCN Red List critically endangered species
- Rhinoceroses
- EDGE species
- Fauna of East Africa
- Mammals of Southern Africa
- Mammals of Sub-Saharan Africa
- Critically endangered fauna of Africa
- Mammals described in 1758
- Species endangered by use in wearables
- Species endangered by human consumption for medicinal or magical purposes
Languages
Missing link (human evolution)
A symbolic portrayal of human evolution, wrongly implying that evolution is linear and progressive.
Phylogenetic tree of hominid evolution
In addition to implying a linear evolution, the term also implies that a particular fossil has not yet been found. Many of the famous discoveries in human evolution are often termed "missing links". For example, there were the Peking Man and the Java Man, despite the fact that these fossils are not missing. Transitional forms that have not been discovered are also termed missing links; however, there is no singular missing link. The scarcity of transitional fossils can be attributed to the incompleteness of the fossil record.
Historical origins
The term "missing link" was influenced by the 18th century Enlightenment thinkers such as Alexander Pope and Jean-Jacques Rousseau who thought of humans as links in the Great Chain of Being. The Great Chain of Being is a hierarchical structure of all matter and life. Influenced by Aristotle's theory of higher and lower animals, the Great Chain of Being was created during the Medieval period in Europe and was strongly influenced by religious thought.[1] God was at the top of the chain followed by man and then animals. It was during the 18th century that the set nature of species and their immutable place in the great chain was questioned. The dual nature of the chain, divided yet united, had always allowed for seeing creation as essentially one continuous whole, with the potential for overlap between the links.[2] Radical thinkers like Jean-Baptiste Lamarck saw a progression of life forms from the simplest creatures striving towards complexity and perfection, a schema accepted by zoologists like Henri de Blainville.[3] The very idea of an ordering of organisms, even if supposedly fixed, laid the basis for the idea of transmutation of species, for example Charles Darwin's theory of evolution.[4]The earliest publication that explicitly uses the term “missing link” was in 1844 in Vestiges of the Natural History of Creation by Robert Chambers, which uses the term in an evolutionary context relating to gaps in the fossil record.[5] Charles Lyell employed the term a few years later in 1851 in his third edition of Elements of Geology to as a metaphor for the missing gaps in the continuity of the geological column.[6] The first time it was used as a name for transitional types between different taxa was in 1863, in Lyell's Geological Evidences of the Antiquity of Man.[7] "Missing link" later became a name for transitional fossils, particularly those seen as bridging the gulf between man and animal. Subsequently, Charles Darwin, Thomas Henry Huxley, and Ernst Haeckel used it in their works with this meaning.
Historical beliefs about the missing link
Haeckel's Chain of the Animal Ancestors of Man
Haeckel claimed that human evolution occurred in 24 stages and that the 23rd stage was a theoretical missing link he named Pithecanthropus alalus ("ape-man lacking speech").[8] Haeckel claimed the origin of humanity was to be found in Asia. He theorized that the missing link was to be found on the lost continent of Lemuria located in the Indian Ocean. He believed that Lemuria was the home of the first humans and that Asia was the home of many of the earliest primates; he thus supported that Asia was the cradle of hominid evolution. Haeckel argued that humans were closely related to the primates of Southeast Asia and rejected Darwin's hypothesis of human origins in Africa.[1][9]
The search for a fossil that connected man and ape was unproductive until the Dutch paleontologist Eugene Dubois went to Indonesia. Between 1886 and 1895 Dubois discovered remains that he later described as "an intermediate species between humans and monkeys". He named the hominin Pithecanthropus erectus (erect ape-man), which has now been reclassified as Homo erectus. In the media, the Java Man was hailed as the missing link. For instance, the headline of the Philadelphia Enquirer on February 3, 1895, was "The Missing Link: A Dutch Surgeon in Java Unearths the Needed Specimen".[10]
Famous "missing links" in human evolution
Java Man, the original "missing link" found in Java
- Java Man (Homo erectus): Discovered by Eugene Dubois in 1891 in Indonesia. Originally named Pithecanthropus erectus.
- Piltdown Man: A set of bones found in 1912 thought to be the "missing link" between ape and man. Eventually revealed to be a hoax.
- Taung Child (Australopithecus africanus): Discovered by Raymond Dart in 1924 in South Africa.
- Homo habilis (described in 1964) has features intermediate between Australopithecus and Homo erectus, and its classification in Homo rather than Australopithecus has been questioned.[11]
- Lucy (Australopithecus afarensis): Discovered in 1974 by Donald Johanson in Ethiopia
- Australopithecus sediba: A series of skeletons discovered in South Africa between 2008-2010
Portrayals in media
- The Missing Link in Monsters vs. Aliens (2009)
- Missing Link (1988)
- The Missing Link (1927)
- The Missing Link (1980)
- Missing Link (2019)
References
- Wood and Richmond; Richmond, BG (2000). "Human evolution: taxonomy and paleobiology". Journal of Anatomy. 197 (Pt 1): 19–60. doi:10.1046/j.1469-7580.2000.19710019.x. PMC 1468107. PMID 10999270. p. 41: "A recent reassessment of cladistic and functional evidence concluded that there are few, if any, grounds for retaining H. habilis in Homo, and recommended that the material be transferred (or, for some, returned) to Australopithecus (Wood & Collard, 1999)."
(*)
Einstein's Theory of Special Relativity | Space
www.space.com › 36273-theory-special-relativity
Special relativity
Jump to navigation
Jump to search
In physics, special relativity (also known as the special theory of relativity) is the generally accepted and experimentally confirmed physical theory regarding the relationship between space and time. In Albert Einstein's original treatment, it is based on two postulates:
Special relativity was originally proposed by Albert Einstein in a paper published on 26 September 1905 titled "On the Electrodynamics of Moving Bodies".[p 1] The incompatibility of Newtonian mechanics with Maxwell's equations of electromagnetism and, experimentally, the Michelson-Morley null result (and subsequent similar experiments) demonstrated that the historically hypothesized luminiferous aether did not exist. This led to Einstein's development of special relativity, which corrects mechanics to handle situations involving all motions and especially those at a speed close to that of light (known as relativistic velocities). Today, special relativity is proven to be the most accurate model of motion at any speed when gravitational effects are negligible. Even so, the Newtonian model is still valid as a simple and accurate approximation at low velocities (relative to the speed of light), for example, everyday motions on Earth.
Special relativity has a wide range of consequences. These have been experimentally verified,[1] and include length contraction, time dilation, relativistic mass, a universal speed limit, mass–energy equivalence, the speed of causality and relativity of simultaneity. It has, for example, replaced the conventional notion of an absolute universal time with the notion of a time that is dependent on reference frame and spatial position. Rather than an invariant time interval between two events, there is an invariant spacetime interval. Combined with other laws of physics, the two postulates of special relativity predict the equivalence of mass and energy, as expressed in the mass–energy equivalence formula E = mc2 (c is the speed of light in a vacuum).[2][3]
A defining feature of special relativity is the replacement of the Galilean transformations of Newtonian mechanics with the Lorentz transformations. Time and space cannot be defined separately from each other (as was earlier thought to be the case). Rather, space and time are interwoven into a single continuum known as "spacetime". Events that occur at the same time for one observer can occur at different times for another.
Until Einstein developed general relativity, introducing a curved spacetime to incorporate gravity, the phrase "special relativity" was not used. A translation sometimes used is "restricted relativity"; "special" really means "special case".[p 2][p 3][p 4][note 1]
The theory is "special" in that it only applies in the special case where the spacetime is "flat", that is, the curvature of spacetime, described by the energy-momentum tensor and causing gravity, is negligible.[4][note 2] In order to correctly accommodate gravity, Einstein formulated general relativity in 1915. Special relativity, contrary to some historical descriptions, does accommodate accelerations as well as accelerating frames of reference.[5][6]
Just as Galilean relativity is now accepted to be an approximation of special relativity that is valid for low speeds, special relativity is considered an approximation of general relativity that is valid for weak gravitational fields, that is, at a sufficiently small scale (e.g., for tidal forces) and in conditions of free fall. General relativity, however, incorporates noneuclidean geometry in order to represent gravitational effects as the geometric curvature of spacetime. Special relativity is restricted to the flat spacetime known as Minkowski space. As long as the universe can be modeled as a pseudo-Riemannian manifold, a Lorentz-invariant frame that abides by special relativity can be defined for a sufficiently small neighborhood of each point in this curved spacetime.
Galileo Galilei had already postulated that there is no absolute and well-defined state of rest (no privileged reference frames), a principle now called Galileo's principle of relativity. Einstein extended this principle so that it accounted for the constant speed of light,[7] a phenomenon that had been observed in the Michelson–Morley experiment. He also postulated that it holds for all the laws of physics, including both the laws of mechanics and of electrodynamics.[8]
| Special relativity |
|---|
 |
- the laws of physics are invariant (i.e., identical) in all inertial frames of reference (i.e., non-accelerating frames of reference); and
- the speed of light in a vacuum is the same for all observers, regardless of the motion of the light source or observer.
Special relativity was originally proposed by Albert Einstein in a paper published on 26 September 1905 titled "On the Electrodynamics of Moving Bodies".[p 1] The incompatibility of Newtonian mechanics with Maxwell's equations of electromagnetism and, experimentally, the Michelson-Morley null result (and subsequent similar experiments) demonstrated that the historically hypothesized luminiferous aether did not exist. This led to Einstein's development of special relativity, which corrects mechanics to handle situations involving all motions and especially those at a speed close to that of light (known as relativistic velocities). Today, special relativity is proven to be the most accurate model of motion at any speed when gravitational effects are negligible. Even so, the Newtonian model is still valid as a simple and accurate approximation at low velocities (relative to the speed of light), for example, everyday motions on Earth.
Special relativity has a wide range of consequences. These have been experimentally verified,[1] and include length contraction, time dilation, relativistic mass, a universal speed limit, mass–energy equivalence, the speed of causality and relativity of simultaneity. It has, for example, replaced the conventional notion of an absolute universal time with the notion of a time that is dependent on reference frame and spatial position. Rather than an invariant time interval between two events, there is an invariant spacetime interval. Combined with other laws of physics, the two postulates of special relativity predict the equivalence of mass and energy, as expressed in the mass–energy equivalence formula E = mc2 (c is the speed of light in a vacuum).[2][3]
A defining feature of special relativity is the replacement of the Galilean transformations of Newtonian mechanics with the Lorentz transformations. Time and space cannot be defined separately from each other (as was earlier thought to be the case). Rather, space and time are interwoven into a single continuum known as "spacetime". Events that occur at the same time for one observer can occur at different times for another.
Until Einstein developed general relativity, introducing a curved spacetime to incorporate gravity, the phrase "special relativity" was not used. A translation sometimes used is "restricted relativity"; "special" really means "special case".[p 2][p 3][p 4][note 1]
The theory is "special" in that it only applies in the special case where the spacetime is "flat", that is, the curvature of spacetime, described by the energy-momentum tensor and causing gravity, is negligible.[4][note 2] In order to correctly accommodate gravity, Einstein formulated general relativity in 1915. Special relativity, contrary to some historical descriptions, does accommodate accelerations as well as accelerating frames of reference.[5][6]
Just as Galilean relativity is now accepted to be an approximation of special relativity that is valid for low speeds, special relativity is considered an approximation of general relativity that is valid for weak gravitational fields, that is, at a sufficiently small scale (e.g., for tidal forces) and in conditions of free fall. General relativity, however, incorporates noneuclidean geometry in order to represent gravitational effects as the geometric curvature of spacetime. Special relativity is restricted to the flat spacetime known as Minkowski space. As long as the universe can be modeled as a pseudo-Riemannian manifold, a Lorentz-invariant frame that abides by special relativity can be defined for a sufficiently small neighborhood of each point in this curved spacetime.
Galileo Galilei had already postulated that there is no absolute and well-defined state of rest (no privileged reference frames), a principle now called Galileo's principle of relativity. Einstein extended this principle so that it accounted for the constant speed of light,[7] a phenomenon that had been observed in the Michelson–Morley experiment. He also postulated that it holds for all the laws of physics, including both the laws of mechanics and of electrodynamics.[8]
Albert Einstein around 1905, the year his "Annus Mirabilis papers" were published. These included Zur Elektrodynamik bewegter Körper, the paper founding special relativity.
Traditional "two postulates" approach to special relativity
Reflections of this type made it clear to me as long ago as shortly after 1900, i.e., shortly after Planck's trailblazing work, that neither mechanics nor electrodynamics could (except in limiting cases) claim exact validity. Gradually I despaired of the possibility of discovering the true laws by means of constructive efforts based on known facts. The longer and the more desperately I tried, the more I came to the conviction that only the discovery of a universal formal principle could lead us to assured results ... How, then, could such a universal principle be found?Einstein discerned two fundamental propositions that seemed to be the most assured, regardless of the exact validity of the (then) known laws of either mechanics or electrodynamics. These propositions were the constancy of the speed of light in a vacuum and the independence of physical laws (especially the constancy of the speed of light) from the choice of inertial system. In his initial presentation of special relativity in 1905 he expressed these postulates as:[p 1]
— Albert Einstein: Autobiographical Notes[p 5]
- The Principle of Relativity – the laws by which the states of physical systems undergo change are not affected, whether these changes of state be referred to the one or the other of two systems in uniform translatory motion relative to each other.[p 1]
- The Principle of Invariant Light Speed – "... light is always propagated in empty space with a definite velocity [speed] c which is independent of the state of motion of the emitting body" (from the preface).[p 1] That is, light in vacuum propagates with the speed c (a fixed constant, independent of direction) in at least one system of inertial coordinates (the "stationary system"), regardless of the state of motion of the light source.
The derivation of special relativity depends not only on these two explicit postulates, but also on several tacit assumptions (made in almost all theories of physics), including the isotropy and homogeneity of space and the independence of measuring rods and clocks from their past history.[p 6]
Following Einstein's original presentation of special relativity in 1905, many different sets of postulates have been proposed in various alternative derivations.[11] However, the most common set of postulates remains those employed by Einstein in his original paper. A more mathematical statement of the Principle of Relativity made later by Einstein, which introduces the concept of simplicity not mentioned above is:
Special principle of relativity: If a system of coordinates K is chosen so that, in relation to it, physical laws hold good in their simplest form, the same laws hold good in relation to any other system of coordinates K′ moving in uniform translation relatively to K.[12]Henri Poincaré provided the mathematical framework for relativity theory by proving that Lorentz transformations are a subset of his Poincaré group of symmetry transformations. Einstein later derived these transformations from his axioms.
Many of Einstein's papers present derivations of the Lorentz transformation based upon these two principles.[p 7]
Principle of relativity
Reference frames and relative motion
Figure 2-1. The primed system is in motion relative to the unprimed system with constant velocity v only along the x-axis, from the perspective of an observer stationary in the unprimed system. By the principle of relativity, an observer stationary in the primed system will view a likewise construction except that the velocity they record will be −v.
The changing of the speed of propagation of interaction from infinite
in non-relativistic mechanics to a finite value will require a
modification of the transformation equations mapping events in one frame
to another.
An event is an occurrence that can be assigned a single unique moment and location in space relative to a reference frame: it is a "point" in spacetime. Since the speed of light is constant in relativity irrespective of reference frame, pulses of light can be used to unambiguously measure distances and refer back the times that events occurred to the clock, even though light takes time to reach the clock after the event has transpired.
For example, the explosion of a firecracker may be considered to be an "event". We can completely specify an event by its four spacetime coordinates: The time of occurrence and its 3-dimensional spatial location define a reference point. Let's call this reference frame S.
In relativity theory, we often want to calculate the coordinates of an event from differing reference frames. The equations that relate measurements made in different frames are called transformation equations.
Standard configuration
To gain insight in how the spacetime coordinates measured by observers in different reference frames compare with each other, it is useful to work with a simplified setup with frames in a standard configuration.[13]:107 With care, this allows simplification of the math with no loss of generality in the conclusions that are reached. In Fig. 2‑1, two Galilean reference frames (i.e., conventional 3-space frames) are displayed in relative motion. Frame S belongs to a first observer O, and frame S′ (pronounced "S prime" or "S dash") belongs to a second observer O′.- The x, y, z axes of frame S are oriented parallel to the respective primed axes of frame S′.
- Frame S′ moves, for simplicity, in a single direction: the x-direction of frame S with a constant velocity v as measured in frame S.
- The origins of frames S and S′ are coincident when time t = 0 for frame S and t′ = 0 for frame S′.
Lack of an absolute reference frame
The principle of relativity, which states that physical laws have the same form in each inertial reference frame, dates back to Galileo, and was incorporated into Newtonian physics. However, in the late 19th century, the existence of electromagnetic waves led some physicists to suggest that the universe was filled with a substance that they called "aether", which, they postulated, would act as the medium through which these waves, or vibrations, propagated (in many respects similar to the way sound propagates through air). The aether was thought to be an absolute reference frame against which all speeds could be measured, and could be considered fixed and motionless relative to Earth or some other fixed reference point. The aether supposedly possessed some wonderful properties: it was sufficiently elastic to support electromagnetic waves, and those waves could interact with matter, yet it offered no resistance to bodies passing through it (its one property was that it allowed electromagnetic waves to propagate). The results of various experiments, including the Michelson–Morley experiment in 1887 (subsequently verified with more accurate and innovative experiments), led to the theory of special relativity, by showing that the aether did not exist.[14] Einstein's solution was to discard the notion of an aether and the absolute state of rest. In relativity, any reference frame moving with uniform motion will observe the same laws of physics. In particular, the speed of light in vacuum is always measured to be c, even when measured by multiple systems that are moving at different (but constant) velocities.Relativity without the second postulate
From the principle of relativity alone without assuming the constancy of the speed of light (i.e., using the isotropy of space and the symmetry implied by the principle of special relativity) it can be shown that the spacetime transformations between inertial frames are either Euclidean, Galilean, or Lorentzian. In the Lorentzian case, one can then obtain relativistic interval conservation and a certain finite limiting speed. Experiments suggest that this speed is the speed of light in vacuum.[p 8][15]Lorentz invariance as the essential core of special relativity
Alternative approaches to special relativity
Einstein consistently based the derivation of Lorentz invariance (the essential core of special relativity) on just the two basic principles of relativity and light-speed invariance. He wrote:The insight fundamental for the special theory of relativity is this: The assumptions relativity and light speed invariance are compatible if relations of a new type ("Lorentz transformation") are postulated for the conversion of coordinates and times of events ... The universal principle of the special theory of relativity is contained in the postulate: The laws of physics are invariant with respect to Lorentz transformations (for the transition from one inertial system to any other arbitrarily chosen inertial system). This is a restricting principle for natural laws ...[p 5]Thus many modern treatments of special relativity base it on the single postulate of universal Lorentz covariance, or, equivalently, on the single postulate of Minkowski spacetime.[p 9][p 10]
Rather than considering universal Lorentz covariance to be a derived principle, this article considers it to be the fundamental postulate of special relativity. The traditional two-postulate approach to special relativity is presented in innumerable college textbooks and popular presentations.[16] Textbooks starting with the single postulate of Minkowski spacetime include those by Taylor and Wheeler[17] and by Callahan.[18] This is also the approach followed by the Wikipedia articles Spacetime and Minkowski diagram.
Lorentz transformation and its inverse
Define an event to have spacetime coordinates (t,x,y,z) in system S and (t′,x′,y′,z′) in a reference frame moving at a velocity v with respect to that frame, S′. Then the Lorentz transformation specifies that these coordinates are related in the following way:Solving the four transformation equations above for the unprimed coordinates yields the inverse Lorentz transformation:
There is nothing special about the x-axis. The transformation can apply to the y- or z-axis, or indeed in any direction parallel to the motion (which are warped by the γ factor) and perpendicular; see the article Lorentz transformation for details.
A quantity invariant under Lorentz transformations is known as a Lorentz scalar.
Writing the Lorentz transformation and its inverse in terms of coordinate differences, where one event has coordinates (x1, t1) and (x′1, t′1), another event has coordinates (x2, t2) and (x′2, t′2), and the differences are defined as
- Eq. 1:
- Eq. 2:
- Eq. 3:
- Eq. 4:
- Eq. 5:
- Eq. 6:
Graphical representation of the Lorentz transformation
Figure 3-1. Drawing a Minkowski spacetime diagram to illustrate a Lorentz transformation.
To draw a spacetime diagram, begin by considering two Galilean reference frames, S and S', in standard configuration, as shown in Fig. 2‑1.[15][19]:155–199
Fig. 3‑1a. Draw the
 and
and  axes of frame S. The
axes of frame S. The  axis is horizontal and the
axis is horizontal and the  (actually
(actually  ) axis is vertical, which is the opposite of the usual convention in kinematics. The
) axis is vertical, which is the opposite of the usual convention in kinematics. The  axis is scaled by a factor of
axis is scaled by a factor of  so that both axes have common units of length. In the diagram shown,
the gridlines are spaced one unit distance apart. The 45° diagonal lines
represent the worldlines of two photons passing through the origin at time
so that both axes have common units of length. In the diagram shown,
the gridlines are spaced one unit distance apart. The 45° diagonal lines
represent the worldlines of two photons passing through the origin at time  The slope of these worldlines is 1 because the photons advance one unit in space per unit of time. Two events,
The slope of these worldlines is 1 because the photons advance one unit in space per unit of time. Two events,  and
and  have been plotted on this graph so that their coordinates may be compared in the S and S' frames.
have been plotted on this graph so that their coordinates may be compared in the S and S' frames.
Fig. 3‑1b. Draw the
 and
and  axes of frame S'. The
axes of frame S'. The  axis represents the worldline of the origin of the S' coordinate system as measured in frame S. In this figure,
axis represents the worldline of the origin of the S' coordinate system as measured in frame S. In this figure,  Both the
Both the  and
and  axes are tilted from the unprimed axes by an angle
axes are tilted from the unprimed axes by an angle  where
where  The primed and unprimed axes share a common origin because frames S and S' had been set up in standard configuration, so that
The primed and unprimed axes share a common origin because frames S and S' had been set up in standard configuration, so that  when
when 
Fig. 3‑1c. Units in the primed axes have a different scale from units in the unprimed axes. From the Lorentz transformations, we observe that
 coordinates of
coordinates of  in the primed coordinate system transform to
in the primed coordinate system transform to  in the unprimed coordinate system. Likewise,
in the unprimed coordinate system. Likewise,  coordinates of
coordinates of  in the primed coordinate system transform to
in the primed coordinate system transform to  in the unprimed system. Draw gridlines parallel with the
in the unprimed system. Draw gridlines parallel with the  axis through points
axis through points  as measured in the unprimed frame, where
as measured in the unprimed frame, where  is an integer. Likewise, draw gridlines parallel with the
is an integer. Likewise, draw gridlines parallel with the  axis through
axis through  as measured in the unprimed frame. Using the Pythagorean theorem, we observe that the spacing between
as measured in the unprimed frame. Using the Pythagorean theorem, we observe that the spacing between  units equals
units equals  times the spacing between
times the spacing between  units, as measured in frame S. This ratio is always greater than 1, and ultimately it approaches infinity as
units, as measured in frame S. This ratio is always greater than 1, and ultimately it approaches infinity as 
Fig. 3‑1d. Since the speed of light is an invariant, the worldlines of two photons passing through the origin at time
 still plot as 45° diagonal lines. The primed coordinates of
still plot as 45° diagonal lines. The primed coordinates of  and
and  are related to the unprimed coordinates through the Lorentz transformations and could
be approximately measured from the graph (assuming that it has been
plotted accurately enough), but the real merit of a Minkowski diagram is
its granting us a geometric view of the scenario. For example, in this
figure, we observe that the two timelike-separated events that had
different x-coordinates in the unprimed frame are now at the same
position in space.
are related to the unprimed coordinates through the Lorentz transformations and could
be approximately measured from the graph (assuming that it has been
plotted accurately enough), but the real merit of a Minkowski diagram is
its granting us a geometric view of the scenario. For example, in this
figure, we observe that the two timelike-separated events that had
different x-coordinates in the unprimed frame are now at the same
position in space.
While the unprimed frame is drawn with space and time axes that meet at right angles, the primed frame is drawn with axes that meet at acute or obtuse angles. The frames are actually equivalent. The asymmetry is due to unavoidable distortions in how spacetime coordinates map onto a Cartesian plane. By analogy, planar maps of the world are unavoidably distorted, but with experience and intuition, one learns to mentally account for these distortions.
Consequences derived from the Lorentz transformation
The consequences of special relativity can be derived from the Lorentz transformation equations.[20] These transformations, and hence special relativity, lead to different physical predictions than those of Newtonian mechanics at all relative velocities, and most pronounced when relative velocities become comparable to the speed of light. The speed of light is so much larger than anything most humans encounter that some of the effects predicted by relativity are initially counterintuitive.Invariant interval
In Galilean relativity, length ( )[note 3] and temporal separation between two events (
)[note 3] and temporal separation between two events ( ) are independent invariants, the values of which do not change when observed from different frames of reference.[note 4][note 5]
) are independent invariants, the values of which do not change when observed from different frames of reference.[note 4][note 5]
In special relativity, however, the interweaving of spatial and temporal coordinates generates the concept of an invariant interval, denoted as
 :
:
The interweaving of space and time revokes the implicitly assumed concepts of absolute simultaneity and synchronization across non-comoving frames.
The form of
 being the difference
of the squared time lapse and the squared spatial distance,
demonstrates a fundamental discrepancy between Euclidean and spacetime
distances.[note 7] The invariance of this interval is a property of the general Lorentz transform (also called the Poincaré transformation), making it an isometry
of spacetime. The general Lorentz transform extends the standard
Lorentz transform (which deals with translations without rotation, that
is, Lorentz boosts, in the x-direction) with all other translations, reflections, and rotations between any Cartesian inertial frame.[24]:33–34
being the difference
of the squared time lapse and the squared spatial distance,
demonstrates a fundamental discrepancy between Euclidean and spacetime
distances.[note 7] The invariance of this interval is a property of the general Lorentz transform (also called the Poincaré transformation), making it an isometry
of spacetime. The general Lorentz transform extends the standard
Lorentz transform (which deals with translations without rotation, that
is, Lorentz boosts, in the x-direction) with all other translations, reflections, and rotations between any Cartesian inertial frame.[24]:33–34
In the analysis of simplified scenarios, such as spacetime diagrams, a reduced-dimensionality form of the invariant interval is often employed:
 is hence independent of the frame in which it is measured.
is hence independent of the frame in which it is measured.
In considering the physical significance of
 , there are three cases to note:[15][25]:25–39
, there are three cases to note:[15][25]:25–39
- Δs2 > 0: In this case, the two events are separated by more time than space, and they are hence said to be timelike separated. This implies that
and given the Lorentz transformation
it is evident that there exists a
less than
for which
(in particular,
). In other words, given two events that are timelike separated, it is possible to find a frame in which the two events happen at the same place. In this frame, the separation in time,
is called the proper time.
- Δs2 < 0: In this case, the two events are separated by more space than time, and they are hence said to be spacelike separated. This implies that
and given the Lorentz transformation
there exists a
less than
for which
(in particular,
). In other words, given two events that are spacelike separated, it is possible to find a frame in which the two events happen at the same time. In this frame, the separation in space,
is called the proper distance, or proper length. For values of
greater than and less than
the sign of
changes, meaning that the temporal order of spacelike-separated events changes depending on the frame in which the events are viewed. The temporal order of timelike-separated events, however, is absolute, since the only way that
could be greater than
would be if
- Δs2 = 0: In this case, the two events are said to be lightlike separated. This implies that
and this relationship is frame independent due to the invariance of
From this, we observe that the speed of light is
in every inertial frame. In other words, starting from the assumption of universal Lorentz covariance, the constant speed of light is a derived result, rather than a postulate as in the two-postulates formulation of the special theory.
Relativity of simultaneity
Figure 4-1. The three events (A, B, C) are simultaneous in the reference frame of some observer O. In a reference frame moving at v = 0.3c, as measured by O, the events occur in the order C, B, A. In a reference frame moving at v = -0.5c with respect to O, the events occur in the order A, B, C. The white lines, the lines of simultaneity,
move from the past to the future in the respective frames (green
coordinate axes), highlighting events residing on it. They are the locus
of all events occurring at the same time in the respective frame. The
gray area is the light cone with respect to the origin of all considered
frames.
From Equation 3 (the forward Lorentz transformation in terms of coordinate differences)
The Sagnac effect can be considered a manifestation of the relativity of simultaneity.[26] Since relativity of simultaneity is a first order effect in
 ,[15] instruments based on the Sagnac effect for their operation, such as ring laser gyroscopes and fiber optic gyroscopes, are capable of extreme levels of sensitivity.[p 14]
,[15] instruments based on the Sagnac effect for their operation, such as ring laser gyroscopes and fiber optic gyroscopes, are capable of extreme levels of sensitivity.[p 14]
Time dilation
The time lapse between two events is not invariant from one observer to another, but is dependent on the relative speeds of the observers' reference frames (e.g., the twin paradox which concerns a twin who flies off in a spaceship traveling near the speed of light and returns to discover that the non-traveling twin sibling has aged much more, the paradox being that at constant velocity we are unable to discern which twin is non-traveling and which twin travels).Suppose a clock is at rest in the unprimed system S. The location of the clock on two different ticks is then characterized by Δx = 0. To find the relation between the times between these ticks as measured in both systems, Equation 3 can be used to find:
for events satisfying
Length contraction
The dimensions (e.g., length) of an object as measured by one observer may be smaller than the results of measurements of the same object made by another observer (e.g., the ladder paradox involves a long ladder traveling near the speed of light and being contained within a smaller garage).Similarly, suppose a measuring rod is at rest and aligned along the x-axis in the unprimed system S. In this system, the length of this rod is written as Δx. To measure the length of this rod in the system S′, in which the rod is moving, the distances x′ to the end points of the rod must be measured simultaneously in that system S′. In other words, the measurement is characterized by Δt′ = 0, which can be combined with Equation 3 to find the relation between the lengths Δx and Δx′:
for events satisfying
Time dilation and length contraction are not merely appearances. Time dilation is explicitly related to our way of measuring time intervals between events which occur at the same place in a given coordinate system (called "co-local" events). These time intervals (which can be, and are, actually measured experimentally by relevant observers) are different in another coordinate system moving with respect to the first, unless the events, in addition to being co-local, are also simultaneous. Similarly, length contraction relates to our measured distances between separated but simultaneous events in a given coordinate system of choice. If these events are not co-local, but are separated by distance (space), they will not occur at the same spatial distance from each other when seen from another moving coordinate system.
Lorentz transformation of velocities
Consider two frames S and S′ in standard configuration. A particle in S moves in the x direction with velocity vector What is its velocity
What is its velocity  in frame S′ ?
in frame S′ ?
We can write
- Eq. 7:
- Eq. 8:
 and
and  from Equation 5 into Equation 8, followed by straightforward mathematical manipulations and back-substitution from Equation 7 yields the Lorentz transformation of the speed
from Equation 5 into Equation 8, followed by straightforward mathematical manipulations and back-substitution from Equation 7 yields the Lorentz transformation of the speed  to
to  :
:
- Eq. 9:
 with
with 
- Eq. 10:
 not aligned along the x-axis, we write:[8]:47–49
not aligned along the x-axis, we write:[8]:47–49
- Eq. 11:
- Eq. 12:
- Eq. 13:
- Eq. 14:
 of the two velocities
of the two velocities  and
and  and they replace the formula
and they replace the formula  which is valid in Galilean relativity. Interpreted in such a fashion, they are commonly referred to as the relativistic velocity addition (or composition) formulas, valid for the three axes of S and S′ being aligned with each other (although not necessarily in standard configuration).[8]:47–49
which is valid in Galilean relativity. Interpreted in such a fashion, they are commonly referred to as the relativistic velocity addition (or composition) formulas, valid for the three axes of S and S′ being aligned with each other (although not necessarily in standard configuration).[8]:47–49
We note the following points:
- If an object (e.g., a photon) were moving at the speed of light in one frame (i.e., u = ±c or u′ = ±c), then it would also be moving at the speed of light in any other frame, moving at |v| < c.
- The resultant speed of two velocities with magnitude less than c is always a velocity with magnitude less than c.
- If both |u| and |v| (and then also |u′| and |v′|) are small with respect to the speed of light (that is, e.g., |u/c| ≪ 1), then the intuitive Galilean transformations are recovered from the transformation equations for special relativity
- Attaching a frame to a photon (riding a light beam like Einstein considers) requires special treatment of the transformations.
Thomas rotation
The composition of two non-collinear Lorentz boosts (i.e., two non-collinear Lorentz transformations, neither of which involve rotation) results in a Lorentz transformation that is not a pure boost but is the composition of a boost and a rotation.Thomas rotation results from the relativity of simultaneity. In Fig. 4‑2a, a rod of length
 in its rest frame (i.e., having a proper length of
in its rest frame (i.e., having a proper length of  ) rises vertically along the y‑axis in the ground frame.
) rises vertically along the y‑axis in the ground frame.
In Fig. 4‑2b, the same rod is observed from the frame of a rocket moving at speed
 to the right. If we imagine two clocks situated at the left and right ends of the rod that are synchronized in the frame of the rod, relativity of simultaneity causes the observer in the rocket frame to observe (not see) the clock at the right end of the rod as being advanced in time by
to the right. If we imagine two clocks situated at the left and right ends of the rod that are synchronized in the frame of the rod, relativity of simultaneity causes the observer in the rocket frame to observe (not see) the clock at the right end of the rod as being advanced in time by  and the rod is correspondingly observed as tilted.[25]:98–99
and the rod is correspondingly observed as tilted.[25]:98–99
Unlike second-order relativistic effects such as length contraction or time dilation, this effect becomes quite significant even at fairly low velocities. For example, this can be seen in the spin of moving particles, where Thomas precession is a relativistic correction that applies to the spin of an elementary particle or the rotation of a macroscopic gyroscope, relating the angular velocity of the spin of a particle following a curvilinear orbit to the angular velocity of the orbital motion.[25]:169–174
Thomas rotation provides the resolution to the well-known "meter stick and hole paradox".[p 15][25]:98–99
Causality and prohibition of motion faster than light
Figure 4-3. Light cone
The interval AC in the diagram is 'space-like'; that is, there is a frame of reference in which events A and C occur simultaneously, separated only in space. There are also frames in which A precedes C (as shown) and frames in which C precedes A. However, there are no frames accessible by a Lorentz transformation, in which events A and C occur at the same location. If it were possible for a cause-and-effect relationship to exist between events A and C, then paradoxes of causality would result.
For example, if signals could be sent faster than light, then signals could be sent into the sender's past (observer B in the diagrams).[28][p 16] A variety of causal paradoxes could then be constructed.
Consider the spacetime diagrams in Fig. 4‑4. A and B stand alongside a railroad track, when a high speed train passes by, with C riding in the last car of the train and D riding in the leading car. The world lines of A and B are vertical (ct), distinguishing the stationary position of these observers on the ground, while the world lines of C and D are tilted forwards (ct′), reflecting the rapid motion of the observers C and D stationary in their train, as observed from the ground.
- Fig. 4‑4a. The event of "B passing a message to D", as the
leading car passes by, is at the origin of D's frame. D sends the
message along the train to C in the rear car, using a fictitious
"instantaneous communicator". The worldline of this message is the fat
red arrow along the
axis, which is a line of simultaneity in the primed frames of C and D. In the (unprimed) ground frame the signal arrives earlier than it was sent.
- Fig. 4‑4b. The event of "C passing the message to A", who is
standing by the railroad tracks, is at the origin of their frames. Now A
sends the message along the tracks to B via an "instantaneous
communicator". The worldline of this message is the blue fat arrow,
along the
axis, which is a line of simultaneity for the frames of A and B. As seen from the spacetime diagram, B will receive the message before having sent it out, a violation of causality.[29]
 axis (and the signal from A to B slightly steeper than the
axis (and the signal from A to B slightly steeper than the  axis), it would still be possible for B to receive his message before
he had sent it. By increasing the speed of the train to near light
speeds, the
axis), it would still be possible for B to receive his message before
he had sent it. By increasing the speed of the train to near light
speeds, the  and
and  axes can be squeezed very close to the dashed line representing the
speed of light. With this modified setup, it can be demonstrated that
even signals only slightly faster than the speed of light will result in causality violation.[30]
axes can be squeezed very close to the dashed line representing the
speed of light. With this modified setup, it can be demonstrated that
even signals only slightly faster than the speed of light will result in causality violation.[30]
Therefore, if causality is to be preserved, one of the consequences of special relativity is that no information signal or material object can travel faster than light in vacuum.
This is not to say that all faster than light speeds are impossible. Various trivial situations can be described where some "things" (not actual matter or energy) move faster than light.[31] For example, the location where the beam of a search light hits the bottom of a cloud can move faster than light when the search light is turned rapidly (although this does not violate causality or any other relativistic phenomenon).[32][33]
Optical effects
Dragging effects
Figure 5-1. Highly simplified diagram of Fizeau's 1851 experiment.
In 1851, Fizeau conducted an experiment to answer this question, a simplified representation of which is illustrated in Fig. 5‑1. A beam of light is divided by a beam splitter, and the split beams are passed in opposite directions through a tube of flowing water. They are recombined to form interference fringes, indicating a difference in optical path length, that an observer can view. The experiment demonstrated that dragging of the light by the flowing water caused displacement of the fringes, showing that the motion of the water had affected the speed of the light.
According to the theories prevailing at the time, light traveling through a moving medium would be a simple sum of its speed through the medium plus the speed of the medium. Contrary to expectation, Fizeau found that although light appeared to be dragged by the water, the magnitude of the dragging was much lower than expected. If
 is the speed of light in still water, and
is the speed of light in still water, and  is the speed of the water, and
is the speed of the water, and  is the water-bourne speed of light in the lab frame with the flow of
water adding to or subtracting from the speed of light, then
is the water-bourne speed of light in the lab frame with the flow of
water adding to or subtracting from the speed of light, then
 depends on wavelength, the aether must be capable of sustaining different motions at the same time.[note 8]
A variety of theoretical explanations were proposed to explain
Fresnel's dragging coefficient that were completely at odds with each
other. Even before the Michelson–Morley experiment,
Fizeau's experimental results were among a number of observations that
created a critical situation in explaining the optics of moving bodies.[35]
depends on wavelength, the aether must be capable of sustaining different motions at the same time.[note 8]
A variety of theoretical explanations were proposed to explain
Fresnel's dragging coefficient that were completely at odds with each
other. Even before the Michelson–Morley experiment,
Fizeau's experimental results were among a number of observations that
created a critical situation in explaining the optics of moving bodies.[35]
From the point of view of special relativity, Fizeau's result is nothing but an approximation to Equation 10, the relativistic formula for composition of velocities.[24]
Relativistic aberration of light
Figure 5-2. Illustration of stellar aberration
The classical explanation failed experimental test. Since the aberration angle depends on the relationship between the velocity of the receiver and the speed of the incident light, passage of the incident light through a refractive medium should change the aberration angle. In 1810, Arago used this expected phenomenon in a failed attempt to measure the speed of light,[38] and in 1870, George Airy tested the hypothesis using a water-filled telescope, finding that, against expectation, the measured aberration was identical to the aberration measured with an air-filled telescope.[39] A "cumbrous" attempt to explain these results used the hypothesis of partial aether-drag,[40] but was incompatible with the results of the Michelson–Morley experiment, which apparently demanded complete aether-drag.[41]
Assuming inertial frames, the relativistic expression for the aberration of light is applicable to both the receiver moving and source moving cases. A variety of trigonometrically equivalent formulas have been published. Expressed in terms of the variables in Fig. 5‑2, these include[24]:57–60
OR
OR
Relativistic Doppler effect
Relativistic longitudinal Doppler effect
The classical Doppler effect depends on whether the source, receiver, or both are in motion with respect to the medium. The relativistic Doppler effect is independent of any medium. Nevertheless, relativistic Doppler shift for the longitudinal case, with source and receiver moving directly towards or away from each other, can be derived as if it were the classical phenomenon, but modified by the addition of a time dilation term, and that is the treatment described here.[42][43]Assume the receiver and the source are moving away from each other with a relative speed
 as measured by an observer on the receiver or the source (The sign convention adopted here is that
as measured by an observer on the receiver or the source (The sign convention adopted here is that  is negative if the receiver and the source are moving towards each other). Assume that the source is stationary in the medium. Then
is negative if the receiver and the source are moving towards each other). Assume that the source is stationary in the medium. Then
 is the speed of sound.
is the speed of sound.
For light, and with the receiver moving at relativistic speeds, clocks on the receiver are time dilated relative to clocks at the source. The receiver will measure the received frequency to be
and
is the Lorentz factor.
Transverse Doppler effect
Figure
5-3. Transverse Doppler effect for two scenarios: (a) receiver moving
in a circle around the source; (b) source moving in a circle around the
receiver.
Classically, one might expect that if source and receiver are moving transversely with respect to each other with no longitudinal component to their relative motions, that there should be no Doppler shift in the light arriving at the receiver.
Special relativity predicts otherwise. Fig. 5‑3 illustrates two common variants of this scenario. Both variants can be analyzed using simple time dilation arguments.[15] In Fig. 5‑3a, the receiver observes light from the source as being blueshifted by a factor of
 . In Fig. 5‑3b, the light is redshifted by the same factor.
. In Fig. 5‑3b, the light is redshifted by the same factor.
Measurement versus visual appearance
Time dilation and length contraction are not optical illusions, but genuine effects. Measurements of these effects are not an artifact of Doppler shift, nor are they the result of neglecting to take into account the time it takes light to travel from an event to an observer.Scientists make a fundamental distinction between measurement or observation on the one hand, versus visual appearance, or what one sees. The measured shape of an object is a hypothetical snapshot of all of the object's points as they exist at a single moment in time. The visual appearance of an object, however, is affected by the varying lengths of time that light takes to travel from different points on the object to one's eye.
Figure 5-4. Comparison of the measured length contraction of a cube versus its visual appearance.
Figure 5-5. Galaxy M87 streams out a black-hole-powered jet of electrons and other sub-atomic particles traveling at nearly the speed of light.
Another example where visual appearance is at odds with measurement comes from the observation of apparent superluminal motion in various radio galaxies, BL Lac objects, quasars, and other astronomical objects that eject relativistic-speed jets of matter at narrow angles with respect to the viewer. An apparent optical illusion results giving the appearance of faster than light travel.[48][49][50] In Fig. 5‑5, galaxy M87 streams out a high-speed jet of subatomic particles almost directly towards us, but Penrose–Terrell rotation causes the jet to appear to be moving laterally in the same manner that the appearance of the cube in Fig. 5‑4 has been stretched out.[51]
Dynamics
Section Consequences derived from the Lorentz transformation dealt strictly with kinematics, the study of the motion of points, bodies, and systems of bodies without considering the forces that caused the motion. This section discusses masses, forces, energy and so forth, and as such requires consideration of physical effects beyond those encompassed by the Lorentz transformation itself.Equivalence of mass and energy
As an object's speed approaches the speed of light from an observer's point of view, its relativistic mass increases thereby making it more and more difficult to accelerate it from within the observer's frame of reference.The energy content of an object at rest with mass m equals mc2. Conservation of energy implies that, in any reaction, a decrease of the sum of the masses of particles must be accompanied by an increase in kinetic energies of the particles after the reaction. Similarly, the mass of an object can be increased by taking in kinetic energies.
In addition to the papers referenced above—which give derivations of the Lorentz transformation and describe the foundations of special relativity—Einstein also wrote at least four papers giving heuristic arguments for the equivalence (and transmutability) of mass and energy, for E = mc2.
Mass–energy equivalence is a consequence of special relativity. The energy and momentum, which are separate in Newtonian mechanics, form a four-vector in relativity, and this relates the time component (the energy) to the space components (the momentum) in a non-trivial way. For an object at rest, the energy–momentum four-vector is (E/c, 0, 0, 0): it has a time component which is the energy, and three space components which are zero. By changing frames with a Lorentz transformation in the x direction with a small value of the velocity v, the energy momentum four-vector becomes (E/c, Ev/c2, 0, 0). The momentum is equal to the energy multiplied by the velocity divided by c2. As such, the Newtonian mass of an object, which is the ratio of the momentum to the velocity for slow velocities, is equal to E/c2.
The energy and momentum are properties of matter and radiation, and it is impossible to deduce that they form a four-vector just from the two basic postulates of special relativity by themselves, because these don't talk about matter or radiation, they only talk about space and time. The derivation therefore requires some additional physical reasoning. In his 1905 paper, Einstein used the additional principles that Newtonian mechanics should hold for slow velocities, so that there is one energy scalar and one three-vector momentum at slow velocities, and that the conservation law for energy and momentum is exactly true in relativity. Furthermore, he assumed that the energy of light is transformed by the same Doppler-shift factor as its frequency, which he had previously shown to be true based on Maxwell's equations.[p 1] The first of Einstein's papers on this subject was "Does the Inertia of a Body Depend upon its Energy Content?" in 1905.[p 21] Although Einstein's argument in this paper is nearly universally accepted by physicists as correct, even self-evident, many authors over the years have suggested that it is wrong.[52] Other authors suggest that the argument was merely inconclusive because it relied on some implicit assumptions.[53]
Einstein acknowledged the controversy over his derivation in his 1907 survey paper on special relativity. There he notes that it is problematic to rely on Maxwell's equations for the heuristic mass–energy argument. The argument in his 1905 paper can be carried out with the emission of any massless particles, but the Maxwell equations are implicitly used to make it obvious that the emission of light in particular can be achieved only by doing work. To emit electromagnetic waves, all you have to do is shake a charged particle, and this is clearly doing work, so that the emission is of energy.[p 22][note 10]
How far can one travel from the Earth?
Since one can not travel faster than light, one might conclude that a human can never travel farther from Earth than 40 light years if the traveler is active between the ages of 20 and 60. One would easily think that a traveler would never be able to reach more than the very few solar systems which exist within the limit of 20–40 light years from the earth. But that would be a mistaken conclusion. Because of time dilation, a hypothetical spaceship can travel thousands of light years during the pilot's 40 active years. If a spaceship could be built that accelerates at a constant 1g, it will, after a little less than a year, be travelling at almost the speed of light as seen from Earth. This is described by:Relativity and unifying electromagnetism
Theoretical investigation in classical electromagnetism led to the discovery of wave propagation. Equations generalizing the electromagnetic effects found that finite propagation speed of the E and B fields required certain behaviors on charged particles. The general study of moving charges forms the Liénard–Wiechert potential, which is a step towards special relativity.The Lorentz transformation of the electric field of a moving charge into a non-moving observer's reference frame results in the appearance of a mathematical term commonly called the magnetic field. Conversely, the magnetic field generated by a moving charge disappears and becomes a purely electrostatic field in a comoving frame of reference. Maxwell's equations are thus simply an empirical fit to special relativistic effects in a classical model of the Universe. As electric and magnetic fields are reference frame dependent and thus intertwined, one speaks of electromagnetic fields. Special relativity provides the transformation rules for how an electromagnetic field in one inertial frame appears in another inertial frame.
Maxwell's equations in the 3D form are already consistent with the physical content of special relativity, although they are easier to manipulate in a manifestly covariant form, that is, in the language of tensor calculus.[56]
Theories of relativity and quantum mechanics
Special relativity can be combined with quantum mechanics to form relativistic quantum mechanics and quantum electrodynamics. It is an unsolved problem in physics how general relativity and quantum mechanics can be unified; quantum gravity and a "theory of everything", which require a unification including general relativity too, are active and ongoing areas in theoretical research.The early Bohr–Sommerfeld atomic model explained the fine structure of alkali metal atoms using both special relativity and the preliminary knowledge on quantum mechanics of the time.[57]
In 1928, Paul Dirac constructed an influential relativistic wave equation, now known as the Dirac equation in his honour,[p 24] that is fully compatible both with special relativity and with the final version of quantum theory existing after 1926. This equation not only describe the intrinsic angular momentum of the electrons called spin, it also led to the prediction of the antiparticle of the electron (the positron),[p 24][p 25] and fine structure could only be fully explained with special relativity. It was the first foundation of relativistic quantum mechanics.
On the other hand, the existence of antiparticles leads to the conclusion that relativistic quantum mechanics is not enough for a more accurate and complete theory of particle interactions. Instead, a theory of particles interpreted as quantized fields, called quantum field theory, becomes necessary; in which particles can be created and destroyed throughout space and time.
Status
Special relativity in its Minkowski spacetime is accurate only when the absolute value of the gravitational potential is much less than c2 in the region of interest.[58] In a strong gravitational field, one must use general relativity. General relativity becomes special relativity at the limit of a weak field. At very small scales, such as at the Planck length and below, quantum effects must be taken into consideration resulting in quantum gravity. However, at macroscopic scales and in the absence of strong gravitational fields, special relativity is experimentally tested to extremely high degree of accuracy (10−20)[59] and thus accepted by the physics community. Experimental results which appear to contradict it are not reproducible and are thus widely believed to be due to experimental errors.Special relativity is mathematically self-consistent, and it is an organic part of all modern physical theories, most notably quantum field theory, string theory, and general relativity (in the limiting case of negligible gravitational fields).
Newtonian mechanics mathematically follows from special relativity at small velocities (compared to the speed of light) – thus Newtonian mechanics can be considered as a special relativity of slow moving bodies. See classical mechanics for a more detailed discussion.
Several experiments predating Einstein's 1905 paper are now interpreted as evidence for relativity. Of these it is known Einstein was aware of the Fizeau experiment before 1905,[60] and historians have concluded that Einstein was at least aware of the Michelson–Morley experiment as early as 1899 despite claims he made in his later years that it played no role in his development of the theory.[10]
- The Fizeau experiment (1851, repeated by Michelson and Morley in 1886) measured the speed of light in moving media, with results that are consistent with relativistic addition of colinear velocities.
- The famous Michelson–Morley experiment (1881, 1887) gave further support to the postulate that detecting an absolute reference velocity was not achievable. It should be stated here that, contrary to many alternative claims, it said little about the invariance of the speed of light with respect to the source and observer's velocity, as both source and observer were travelling together at the same velocity at all times.
- The Trouton–Noble experiment (1903) showed that the torque on a capacitor is independent of position and inertial reference frame.
- The Experiments of Rayleigh and Brace (1902, 1904) showed that length contraction doesn't lead to birefringence for a co-moving observer, in accordance with the relativity principle.
- Tests of relativistic energy and momentum – testing the limiting speed of particles
- Ives–Stilwell experiment – testing relativistic Doppler effect and time dilation
- Experimental testing of time dilation – relativistic effects on a fast-moving particle's half-life
- Kennedy–Thorndike experiment – time dilation in accordance with Lorentz transformations
- Hughes–Drever experiment – testing isotropy of space and mass
- Modern searches for Lorentz violation – various modern tests
- Experiments to test emission theory demonstrated that the speed of light is independent of the speed of the emitter.
- Experiments to test the aether drag hypothesis – no "aether flow obstruction".
Technical discussion of spacetime
Geometry of spacetime
Comparison between flat Euclidean space and Minkowski space
Figure 10-1. Orthogonality and rotation of coordinate systems compared between left: Euclidean space through circular angle φ, right: in Minkowski spacetime through hyperbolic angle φ (red lines labelled c denote the worldlines of a light signal, a vector is orthogonal to itself if it lies on this line).[61]
In 3D space, the differential of distance (line element) ds is defined by
The actual form of ds above depends on the metric and on the choices for the X0 coordinate. To make the time coordinate look like the space coordinates, it can be treated as imaginary: X0 = ict (this is called a Wick rotation). According to Misner, Thorne and Wheeler (1971, §2.3), ultimately the deeper understanding of both special and general relativity will come from the study of the Minkowski metric (described below) and to take X0 = ct, rather than a "disguised" Euclidean metric using ict as the time coordinate.
Some authors use X0 = t, with factors of c elsewhere to compensate; for instance, spatial coordinates are divided by c or factors of c±2 are included in the metric tensor.[63] These numerous conventions can be superseded by using natural units where c = 1. Then space and time have equivalent units, and no factors of c appear anywhere.
3D spacetime
Figure 10-2. Three-dimensional dual-cone.
4D spacetime
If we extend this to three spatial dimensions, the null geodesics are the 4-dimensional cone:
Figure 10-3. Concentric spheres, illustrating in 3-space the null geodesics of a 4-dimensional cone in spacetime.
This null dual-cone represents the "line of sight" of a point in space. That is, when we look at the stars and say "The light from that star which I am receiving is X years old", we are looking down this line of sight: a null geodesic. We are looking at an event a distance
 away and a time d/c
in the past. For this reason the null dual cone is also known as the
'light cone'. (The point in the lower left of the Fig. 10‑2 represents
the star, the origin represents the observer, and the line represents
the null geodesic "line of sight".)
away and a time d/c
in the past. For this reason the null dual cone is also known as the
'light cone'. (The point in the lower left of the Fig. 10‑2 represents
the star, the origin represents the observer, and the line represents
the null geodesic "line of sight".)
The cone in the −t region is the information that the point is 'receiving', while the cone in the +t section is the information that the point is 'sending'.
The geometry of Minkowski space can be depicted using Minkowski diagrams, which are useful also in understanding many of the thought-experiments in special relativity.
Note that, in 4d spacetime, the concept of the center of mass becomes more complicated, see center of mass (relativistic).
Physics in spacetime
Transformations of physical quantities between reference frames
Above, the Lorentz transformation for the time coordinate and three space coordinates illustrates that they are intertwined. This is true more generally: certain pairs of "timelike" and "spacelike" quantities naturally combine on equal footing under the same Lorentz transformation.The Lorentz transformation in standard configuration above, that is, for a boost in the x direction, can be recast into matrix form as follows:
The simplest example of a four-vector is the position of an event in spacetime, which constitutes a timelike component ct and spacelike component x = (x, y, z), in a contravariant position four vector with components:
 from 0 to 3, and
from 0 to 3, and  is a matrix.
is a matrix.
More generally, all contravariant components of a four-vector
 transform from one frame to another frame by a Lorentz transformation:
transform from one frame to another frame by a Lorentz transformation:
 defined as the derivative of the position 4-vector with respect to proper time:
defined as the derivative of the position 4-vector with respect to proper time:
 and relativistic momentum
and relativistic momentum  of an object are respectively the timelike and spacelike components of a contravariant four momentum vector:
of an object are respectively the timelike and spacelike components of a contravariant four momentum vector:
The four-acceleration is the proper time derivative of 4-velocity:
The four-gradient of a scalar field φ transforms covariantly rather than contravariantly:
More generally, the covariant components of a 4-vector transform according to the inverse Lorentz transformation:
 is the reciprocal matrix of
is the reciprocal matrix of  .
.
The postulates of special relativity constrain the exact form the Lorentz transformation matrices take.
More generally, most physical quantities are best described as (components of) tensors. So to transform from one frame to another, we use the well-known tensor transformation law[67]
 is the reciprocal matrix of
is the reciprocal matrix of  . All tensors transform by this rule.
. All tensors transform by this rule.
An example of a four dimensional second order antisymmetric tensor is the relativistic angular momentum, which has six components: three are the classical angular momentum, and the other three are related to the boost of the center of mass of the system. The derivative of the relativistic angular momentum with respect to proper time is the relativistic torque, also second order antisymmetric tensor.
The electromagnetic field tensor is another second order antisymmetric tensor field, with six components: three for the electric field and another three for the magnetic field. There is also the stress–energy tensor for the electromagnetic field, namely the electromagnetic stress–energy tensor.
Metric
The metric tensor allows one to define the inner product of two vectors, which in turn allows one to assign a magnitude to the vector. Given the four-dimensional nature of spacetime the Minkowski metric η has components (valid in any inertial reference frame) which can be arranged in a 4 × 4 matrix: , in those frames. Throughout we use the signs as above, different authors use different conventions – see Minkowski metric alternative signs.
, in those frames. Throughout we use the signs as above, different authors use different conventions – see Minkowski metric alternative signs.
The Poincaré group is the most general group of transformations which preserves the Minkowski metric:
The metric can be used for raising and lowering indices on vectors and tensors. Invariants can be constructed using the metric, the inner product of a 4-vector T with another 4-vector S is:
Relativistic kinematics and invariance
The coordinate differentials transform also contravariantly:The 4-velocity Uμ has an invariant form:
Relativistic dynamics and invariance
The invariant magnitude of the momentum 4-vector generates the energy–momentum relation:The rest energy is related to the mass according to the celebrated equation discussed above:
To use Newton's third law of motion, both forces must be defined as the rate of change of momentum with respect to the same time coordinate. That is, it requires the 3D force defined above. Unfortunately, there is no tensor in 4D which contains the components of the 3D force vector among its components.
If a particle is not traveling at c, one can transform the 3D force from the particle's co-moving reference frame into the observer's reference frame. This yields a 4-vector called the four-force. It is the rate of change of the above energy momentum four-vector with respect to proper time. The covariant version of the four-force is:
In a continuous medium, the 3D density of force combines with the density of power to form a covariant 4-vector. The spatial part is the result of dividing the force on a small cell (in 3-space) by the volume of that cell. The time component is −1/c times the power transferred to that cell divided by the volume of the cell. This will be used below in the section on electromagnetism.
See also
- People: Hendrik Lorentz | Henri Poincaré | Albert Einstein | Max Planck | Hermann Minkowski | Max von Laue | Arnold Sommerfeld | Max Born | Gustav Herglotz | Richard C. Tolman
- Relativity: Theory of relativity | History of special relativity | Principle of relativity | Doubly special relativity | General relativity | Frame of reference | Inertial frame of reference | Lorentz transformations | Bondi k-calculus | Einstein synchronisation | Rietdijk–Putnam argument | Special relativity (alternative formulations) | Criticism of relativity theory | Relativity priority dispute
- Physics: Einstein's thought experiments | Newtonian Mechanics | spacetime | speed of light | simultaneity | center of mass (relativistic) | physical cosmology | Doppler effect | relativistic Euler equations | Aether drag hypothesis | Lorentz ether theory | Moving magnet and conductor problem | Shape waves | Relativistic heat conduction | Relativistic disk | Thomas precession | Born rigidity | Born coordinates
- Mathematics: Derivations of the Lorentz transformations | Minkowski space | four-vector | world line | light cone | Lorentz group | Poincaré group | geometry | tensors | split-complex number | Relativity in the APS formalism
- Philosophy: actualism | conventionalism | formalism
- Paradoxes: Twin paradox | Ehrenfest paradox | Ladder paradox | Bell's spaceship paradox | Velocity composition paradox | Lighthouse paradox
Primary sources
- C.D. Anderson (1933). "The Positive Electron". Phys. Rev. 43 (6): 491–494. Bibcode:1933PhRv...43..491A. doi:10.1103/PhysRev.43.491.
References
- Sean M. Carroll (2004). Spacetime and Geometry: An Introduction to General Relativity. Addison Wesley. p. 22. ISBN 978-0-8053-8732-2.
Notes
- In a letter to Carl Seelig in 1955, Einstein wrote "I had already previously found that Maxwell's theory did not account for the micro-structure of radiation and could therefore have no general validity.", Einstein letter to Carl Seelig, 1955.
Textbooks
- Einstein, Albert (1920). Relativity: The Special and General Theory.
- Einstein, Albert (1996). The Meaning of Relativity. Fine Communications. ISBN 1-56731-136-9
- Logunov, Anatoly A. (2005) Henri Poincaré and the Relativity Theory (transl. from Russian by G. Pontocorvo and V. O. Soloviev, edited by V. A. Petrov) Nauka, Moscow.
- Charles Misner, Kip Thorne, and John Archibald Wheeler (1971) Gravitation. W. H. Freeman & Co. ISBN 0-7167-0334-3
- Post, E.J., 1997 (1962) Formal Structure of Electromagnetics: General Covariance and Electromagnetics. Dover Publications.
- Wolfgang Rindler (1991). Introduction to Special Relativity (2nd ed.), Oxford University Press. ISBN 978-0-19-853952-0; ISBN 0-19-853952-5
- Harvey R. Brown (2005). Physical relativity: space–time structure from a dynamical perspective, Oxford University Press, ISBN 0-19-927583-1; ISBN 978-0-19-927583-0
- Qadir, Asghar (1989). Relativity: An Introduction to the Special Theory. Singapore: World Scientific Publications. p. 128. Bibcode:1989rist.book.....Q. ISBN 978-9971-5-0612-4.
- French, A. P. (1968). Special Relativity (M.I.T. Introductory Physics) (1st ed.). W. W. Norton & Company. ISBN 978-0393097931.
- Silberstein, Ludwik (1914) The Theory of Relativity.
- Lawrence Sklar (1977). Space, Time and Spacetime. University of California Press. ISBN 978-0-520-03174-6.
- Lawrence Sklar (1992). Philosophy of Physics. Westview Press. ISBN 978-0-8133-0625-4.
- Sergey Stepanov (2018). Relativistic World. De Gruyter. ISBN 9783110515879.
- Taylor, Edwin, and John Archibald Wheeler (1992) Spacetime Physics (2nd ed.). W.H. Freeman & Co. ISBN 0-7167-2327-1
- Tipler, Paul, and Llewellyn, Ralph (2002). Modern Physics (4th ed.). W. H. Freeman & Co. ISBN 0-7167-4345-0
Journal articles
- Alvager, T.; Farley, F. J. M.; Kjellman, J.; Wallin, L.; et al. (1964). "Test of the Second Postulate of Special Relativity in the GeV region". Physics Letters. 12 (3): 260–262. Bibcode:1964PhL....12..260A. doi:10.1016/0031-9163(64)91095-9.
- Darrigol, Olivier (2004). "The Mystery of the Poincaré–Einstein Connection". Isis. 95 (4): 614–26. doi:10.1086/430652. PMID 16011297.
- Wolf, Peter; Petit, Gerard (1997). "Satellite test of Special Relativity using the Global Positioning System". Physical Review A. 56 (6): 4405–09. Bibcode:1997PhRvA..56.4405W. doi:10.1103/PhysRevA.56.4405.
- Special Relativity Scholarpedia
- Rindler, Wolfgang. "Special relativity: Kinematics". Scholarpedia. 6 (2): 8520. doi:10.4249/scholarpedia.8520.
External links
| Wikisource has original text related to this article: |
| Wikisource has original works on the topic: Relativity |
| Wikibooks has a book on the topic of: Special Relativity |
| Wikiversity has learning resources about Special Relativity |
| Look up special relativity in Wiktionary, the free dictionary. |
Original works
- Zur Elektrodynamik bewegter Körper Einstein's original work in German, Annalen der Physik, Bern 1905
- On the Electrodynamics of Moving Bodies English Translation as published in the 1923 book The Principle of Relativity.
Special relativity for a general audience (no mathematical knowledge required)
- Einstein Light An award-winning, non-technical introduction (film clips and demonstrations) supported by dozens of pages of further explanations and animations, at levels with or without mathematics.
- Einstein Online Introduction to relativity theory, from the Max Planck Institute for Gravitational Physics.
- Audio: Cain/Gay (2006) – Astronomy Cast. Einstein's Theory of Special Relativity
Special relativity explained (using simple or more advanced mathematics)
- Greg Egan's Foundations.
- The Hogg Notes on Special Relativity A good introduction to special relativity at the undergraduate level, using calculus.
- Relativity Calculator: Special Relativity – An algebraic and integral calculus derivation for E = mc2.
- MathPages – Reflections on Relativity A complete online book on relativity with an extensive bibliography.
- Special Relativity An introduction to special relativity at the undergraduate level.
- Relativity: the Special and General Theory at Project Gutenberg, by Albert Einstein
- Special Relativity Lecture Notes is a standard introduction to special relativity containing illustrative explanations based on drawings and spacetime diagrams from Virginia Polytechnic Institute and State University.
- Understanding Special Relativity The theory of special relativity in an easily understandable way.
- An Introduction to the Special Theory of Relativity (1964) by Robert Katz, "an introduction ... that is accessible to any student who has had an introduction to general physics and some slight acquaintance with the calculus" (130 pp; pdf format).
- Lecture Notes on Special Relativity by J D Cresser Department of Physics Macquarie University.
- SpecialRelativity.net - An overview with visualizations and minimal mathematics.
Visualization
- Raytracing Special Relativity Software visualizing several scenarios under the influence of special relativity.
- Real Time Relativity The Australian National University. Relativistic visual effects experienced through an interactive program.
- Spacetime travel A variety of visualizations of relativistic effects, from relativistic motion to black holes.
- Through Einstein's Eyes The Australian National University. Relativistic visual effects explained with movies and images.
- Warp Special Relativity Simulator A computer program to show the effects of traveling close to the speed of light.
- Animation clip on YouTube visualizing the Lorentz transformation.
- Original interactive FLASH Animations from John de Pillis illustrating Lorentz and Galilean frames, Train and Tunnel Paradox, the Twin Paradox, Wave Propagation, Clock Synchronization, etc.
- lightspeed An OpenGL-based program developed to illustrate the effects of special relativity on the appearance of moving objects.
- Animation showing the stars near Earth, as seen from a spacecraft accelerating rapidly to light speed.
Languages
Sidney Coleman; Sheldon L. Glashow (1997). "Cosmic Ray and Neutrino Tests of Special Relativity". Physics Letters B. 405 (3–4): 249–252. arXiv:hep-ph/9703240. Bibcode:1997PhLB..405..249C. doi:10.1016/S0370-2693(97)00638-2.
An overview can be found on this page
Lorentz expected that length contraction would result in compressive strains in an object that should result in measurable effects. Such effects would include optical effects in transparent media, such as optical rotation[p 11] and induction of double refraction,[p 12] and the induction of torques on charged condensers moving at an angle with respect to the aether.[p 12] Lorentz was perplexed by experiments such as the Trouton–Noble experiment and the experiments of Rayleigh and Brace which failed to validate his theoretical expectations.[21]
 .[p 13] Lorentz considered local time not to be "real"; rather, it represented an ad hoc change of variable.[22]:51,80
.[p 13] Lorentz considered local time not to be "real"; rather, it represented an ad hoc change of variable.[22]:51,80
Impressed by Lorentz's "most ingenious idea", Poincaré saw more in local time than a mere mathematical trick. It represented the actual time that would be shown on a moving observer's clocks. On the other hand, Poincaré did not consider this measured time to be the "true time" that would be exhibited by clocks at rest in the aether. Poincaré made no attempt to redefine the concepts of space and time. To Poincaré, Lorentz transformation described the apparent states of the field for a moving observer. True states remained those defined with respect to the ether.[23]
 is also an invariant, generated by a variant of the metric signature of spacetime.
is also an invariant, generated by a variant of the metric signature of spacetime.
year 2006–2012
Geological Evidences of the Antiquity of Man.














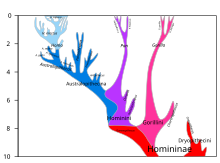




















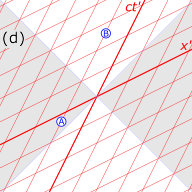










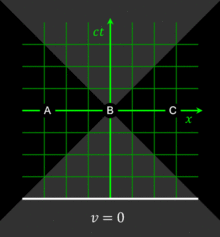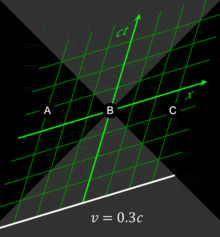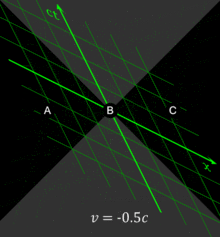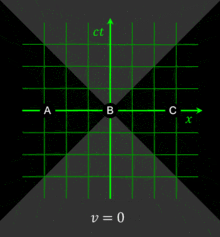

















































































No comments:
Post a Comment