ec=squared
Energy cosmos is not greater than or less than what is Squared, hence four corners earth!! The dynamics of understanding 'equals' measures to the mathematical signs '< >' and as such the temperature of just the infinity sign as a letter would double meaning as ate!! To each of the dynamics of Space/NASA "using data from several telescopes including NASA's Chandra X-ray Observatory, astronomers have caught a supermassive black hole snacking on gas and then "burping" — not once but twice, as described in our latest press release", Hawking's teaching 'matter' does consume per The Black Hole "Jump to Black hole evaporation - when particles escape, the black hole loses a small amount of its energy and therefore some of its mass (mass and energy are related by Einstein's equation E = mc2)", however it is the shape that makes the edit to say more to a galaxy. As energy 'cosmos' examples "The cosmos is the universe. Cosmos is used at times when the universe is regarded as a complex and orderly system or entity; the opposite of chaos." In short the reservation of the pyramid is an interesting vista of blocks representing the constant. It is the constant that would equal 'ec' and that would direct common sense to the relation of those corners on the pyramid as it is the correct shape to visual. In-addition the balance of just the exact measurements makes an apron to such a bib that the curious would have to re-think why the exactness of angle to the absolute fit would not be such a curiosity. As through the study of documentaries and many books the fascination is contained in the cubits and meters although further study would have to be registered as I am not able to compare and measure to the extent that would further this tip of an iceberg yard.
"In geometry, a Johnson solid is a strictly convex polyhedron " as that directs to the "Einstein field equations (EFE; also known as Einstein's equations) comprise the set of 10 equations in Albert Einstein's general theory of relativity that describe the fundamental interaction of gravitation as a result of spacetime being curved by mass and energy." The missing piece is to pause and formulate a new result.
"A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn.[1] Some authors use the terms "convex polytope" and "convex polyhedron" interchangeably, while others prefer to draw a distinction between the notions of a polyhedron and a polytope."
1.) Are the Pyramids equilateral triangles?
A lower symmetry case of the triangular pyramid is C3v, which has an equilateral triangle base, and 3 identical isosceles triangle sides. The square and pentagonal pyramids can also be composed of regular convex polygons, in which case they are Johnson solids.
These twenty-four Greek letters are: Α α, Β β, Γ γ, Δ δ, Ε ε, Ζ ζ, Η η, Θ θ, Ι ι, Κ κ, Λ λ, Μ μ, Ν ν, Ξ ξ, Ο ο, Π π, Ρ ρ, Σ σ/ς, Τ τ, Υ υ, Φ φ, Χ χ, Ψ ψ, and Ω ω.
1A writing system
Ancient Greek: χάος,
Greek χάος means "emptiness, vast void, chasm,[6] abyss", from the verb χαίνω, "gape, be wide open, etc.", from Proto-Indo-European *ǵheh2n-,[7] cognate to Old English geanian, "to gape", whence English yawn.[8]
It may also mean space, the expanse of air, and the nether abyss, infinite darkness.[9] Pherecydes of Syros (fl. 6th century BC) interprets chaos as water, like something formless which can be differentiated.[10]
Einstein field equations
Jump to navigation
Jump to search
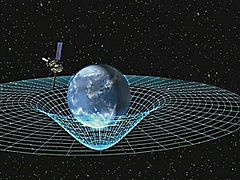
The Einstein field equations (EFE; also known as Einstein's equations) comprise the set of 10 equations in Albert Einstein's general theory of relativity that describe the fundamental interaction of gravitation as a result of spacetime being curved by mass and energy.[1] First published by Einstein in 1915 as a tensor equation,[2] the EFE relate local spacetime curvature (expressed by the Einstein tensor) with the local energy and momentum within that spacetime (expressed by the stress–energy tensor).[3]
Similar to the way that electromagnetic fields are determined using charges and currents via Maxwell's equations, the EFE are used to determine the spacetime geometry resulting from the presence of mass–energy and linear momentum, that is, they determine the metric tensor of spacetime for a given arrangement of stress–energy in the spacetime. The relationship between the metric tensor and the Einstein tensor allows the EFE to be written as a set of non-linear partial differential equations when used in this way. The solutions of the EFE are the components of the metric tensor. The inertial trajectories of particles and radiation (geodesics) in the resulting geometry are then calculated using the geodesic equation.
As well as obeying local energy–momentum conservation, the EFE reduce to Newton's law of gravitation where the gravitational field is weak and velocities are much less than the speed of light.[4]
Exact solutions for the EFE can only be found under simplifying assumptions such as symmetry. Special classes of exact solutions are most often studied as they model many gravitational phenomena, such as rotating black holes and the expanding universe. Further simplification is achieved in approximating the actual spacetime as flat spacetime with a small deviation, leading to the linearized EFE. These equations are used to study phenomena such as gravitational waves.
| Part of a series of articles about |
| General relativity |
|---|
 |
Similar to the way that electromagnetic fields are determined using charges and currents via Maxwell's equations, the EFE are used to determine the spacetime geometry resulting from the presence of mass–energy and linear momentum, that is, they determine the metric tensor of spacetime for a given arrangement of stress–energy in the spacetime. The relationship between the metric tensor and the Einstein tensor allows the EFE to be written as a set of non-linear partial differential equations when used in this way. The solutions of the EFE are the components of the metric tensor. The inertial trajectories of particles and radiation (geodesics) in the resulting geometry are then calculated using the geodesic equation.
As well as obeying local energy–momentum conservation, the EFE reduce to Newton's law of gravitation where the gravitational field is weak and velocities are much less than the speed of light.[4]
Exact solutions for the EFE can only be found under simplifying assumptions such as symmetry. Special classes of exact solutions are most often studied as they model many gravitational phenomena, such as rotating black holes and the expanding universe. Further simplification is achieved in approximating the actual spacetime as flat spacetime with a small deviation, leading to the linearized EFE. These equations are used to study phenomena such as gravitational waves.
Contents
Mathematical form
| Part of a series on |
| Spacetime |
|---|
 |
| General relativity Special relativity Doubly special relativity |
EFE on a wall in Leiden
The EFE is a tensor equation relating a set of symmetric 4 × 4 tensors. Each tensor has 10 independent components. The four Bianchi identities reduce the number of independent equations from 10 to 6, leaving the metric with four gauge fixing degrees of freedom, which correspond to the freedom to choose a coordinate system.
Although the Einstein field equations were initially formulated in the context of a four-dimensional theory, some theorists have explored their consequences in n dimensions.[6] The equations in contexts outside of general relativity are still referred to as the Einstein field equations. The vacuum field equations (obtained when T is identically zero) define Einstein manifolds.
Despite the simple appearance of the equations they are actually quite complicated. Given a specified distribution of matter and energy in the form of a stress–energy tensor, the EFE are understood to be equations for the metric tensor gμν, as both the Ricci tensor and scalar curvature depend on the metric in a complicated nonlinear manner. In fact, when fully written out, the EFE are a system of ten coupled, nonlinear, hyperbolic-elliptic partial differential equations.[citation needed]
One can write the EFE in a more compact form by defining the Einstein tensor
Using geometrized units where G = c = 1, this can be rewritten as
These equations, together with the geodesic equation,[7] which dictates how freely-falling matter moves through space-time, form the core of the mathematical formulation of general relativity.
Sign convention
The above form of the EFE is the standard established by Misner, Thorne, and Wheeler.[8] The authors analyzed all conventions that exist and classified according to the following three signs (S1, S2, S3):Authors including Einstein have used a different sign in their definition for the Ricci tensor which results in the sign of the constant on the right side being negative
Equivalent formulations
Taking the trace with respect to the metric of both sides of the EFE one getsThe cosmological constant
Einstein modified his original field equations to include a cosmological constant term Λ proportional to the metricThe cosmological constant term was originally introduced by Einstein to allow for a universe that is not expanding or contracting. This effort was unsuccessful because:
- the universe described by this theory was unstable, and
- observations by Edwin Hubble confirmed that our universe is expanding.
Despite Einstein's motivation for introducing the cosmological constant term, there is nothing inconsistent with the presence of such a term in the equations. For many years the cosmological constant was almost universally considered to be 0. However, recent improved astronomical techniques have found that a positive value of Λ is needed to explain the accelerating universe.[12][13]
Einstein thought of the cosmological constant as an independent parameter, but its term in the field equation can also be moved algebraically to the other side, written as part of the stress–energy tensor:
Features
Conservation of energy and momentum
General relativity is consistent with the local conservation of energy and momentum expressed as.
Derivation of local energy-momentum conservation
Nonlinearity
The nonlinearity of the EFE distinguishes general relativity from many other fundamental physical theories. For example, Maxwell's equations of electromagnetism are linear in the electric and magnetic fields, and charge and current distributions (i.e. the sum of two solutions is also a solution); another example is Schrödinger's equation of quantum mechanics which is linear in the wavefunction.The correspondence principle
The EFE reduce to Newton's law of gravity by using both the weak-field approximation and the slow-motion approximation. In fact, the constant G appearing in the EFE is determined by making these two approximations.Derivation of Newton's law of gravity
Vacuum field equations
A Swiss commemorative coin from 1979, showing the vacuum field equations with zero cosmological constant (top).
Manifolds with a vanishing Ricci tensor, Rμν = 0, are referred to as Ricci-flat manifolds and manifolds with a Ricci tensor proportional to the metric as Einstein manifolds.
Einstein–Maxwell equations
If the energy-momentum tensor Tμν is that of an electromagnetic field in free space, i.e. if the electromagnetic stress–energy tensorSolutions
The solutions of the Einstein field equations are metrics of spacetime. These metrics describe the structure of the spacetime including the inertial motion of objects in the spacetime. As the field equations are non-linear, they cannot always be completely solved (i.e. without making approximations). For example, there is no known complete solution for a spacetime with two massive bodies in it (which is a theoretical model of a binary star system, for example). However, approximations are usually made in these cases. These are commonly referred to as post-Newtonian approximations. Even so, there are numerous cases where the field equations have been solved completely, and those are called exact solutions.[6]The study of exact solutions of Einstein's field equations is one of the activities of cosmology. It leads to the prediction of black holes and to different models of evolution of the universe.
One can also discover new solutions of the Einstein field equations via the method of orthonormal frames as pioneered by Ellis and MacCallum.[16] In this approach, the Einstein field equations are reduced to a set of coupled, nonlinear, ordinary differential equations. As discussed by Hsu and Wainwright,[17] self-similar solutions to the Einstein field equations are fixed points of the resulting dynamical system. New solutions have been discovered using these methods by LeBlanc [18] and Kohli and Haslam.[19]
The linearized EFE
The nonlinearity of the EFE makes finding exact solutions difficult. One way of solving the field equations is to make an approximation, namely, that far from the source(s) of gravitating matter, the gravitational field is very weak and the spacetime approximates that of Minkowski space. The metric is then written as the sum of the Minkowski metric and a term representing the deviation of the true metric from the Minkowski metric, with terms that are quadratic in or higher powers of the deviation being ignored. This linearization procedure can be used to investigate the phenomena of gravitational radiation.Polynomial form
One might think that EFE are non-polynomial since they contain the inverse of the metric tensor. However, the equations can be arranged so that they contain only the metric tensor and not its inverse. First, the determinant of the metric in 4 dimensions can be written:See also
Notes
- Katanaev, M. O. (July 7, 2005). "Polynomial form of the Hilbert–Einstein action". Gen. Rel. Grav. 38: 1233–1240. arXiv:gr-qc/0507026. Bibcode:2006GReGr..38.1233K. doi:10.1007/s10714-006-0310-5.
References
See General relativity resources.- Misner, Charles W.; Thorne, Kip S.; Wheeler, John Archibald (1973). Gravitation. San Francisco: W. H. Freeman. ISBN 978-0-7167-0344-0.
- Weinberg, Steven (1972). Gravitation and Cosmology. John Wiley & Sons. ISBN 0-471-92567-5.
- Peacock, John A. (1994). Cosmological Physics. Cambridge University Press. ISBN 978-0521410724.
External links
| Wikibooks has a book on the topic of: General Relativity |
| Wikiversity has learning resources about General Relativity |
- Hazewinkel, Michiel, ed. (2001) [1994], "Einstein equations", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4
- Caltech Tutorial on Relativity — A simple introduction to Einstein's Field Equations.
- The Meaning of Einstein's Equation — An explanation of Einstein's field equation, its derivation, and some of its consequences
- Video Lecture on Einstein's Field Equations by MIT Physics Professor Edmund Bertschinger.
- Arch and scaffold: How Einstein found his field equations Physics Today November 2015, History of the Development of the Field Equations
- The Einstein field equation on the wall of the Museum Boerhaave in downtown Leiden










![{\displaystyle {\begin{aligned}g_{\mu \nu }&=[S1]\times \operatorname {diag} (-1,+1,+1,+1)\\[6pt]{R^{\mu }}_{\alpha \beta \gamma }&=[S2]\times \left(\Gamma _{\alpha \gamma ,\beta }^{\mu }-\Gamma _{\alpha \beta ,\gamma }^{\mu }+\Gamma _{\sigma \beta }^{\mu }\Gamma _{\gamma \alpha }^{\sigma }-\Gamma _{\sigma \gamma }^{\mu }\Gamma _{\beta \alpha }^{\sigma }\right)\\[6pt]G_{\mu \nu }&=[S3]\times {\frac {8\pi G}{c^{4}}}T_{\mu \nu }\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a92147546b1d644a097fe983f5b6ba27ee31ea99)
![R_{\mu \nu }=[S2]\times [S3]\times {R^{\alpha }}_{\mu \alpha \nu }](https://wikimedia.org/api/rest_v1/media/math/render/svg/55a370597ca453317d8e0203c784eac935102a37)








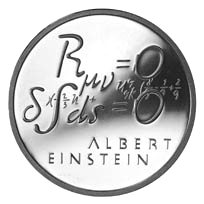




![{\displaystyle {\begin{aligned}{F^{\alpha \beta }}_{;\beta }&=0\\F_{[\alpha \beta ;\gamma ]}&={\tfrac {1}{3}}\left(F_{\alpha \beta ;\gamma }+F_{\beta \gamma ;\alpha }+F_{\gamma \alpha ;\beta }\right)={\tfrac {1}{3}}\left(F_{\alpha \beta ,\gamma }+F_{\beta \gamma ,\alpha }+F_{\gamma \alpha ,\beta }\right)=0.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3151562dc243162c7975eb508847246bd11a013)











No comments:
Post a Comment