Srinivasa Ramanujan | |
|---|---|
 | |
| Born | 22 December 1887 |
| Died | 26 April 1920 (aged 32) |
| Other names | Srinivasa Ramanujan Aiyangar |
| Citizenship | British Raj |
| Education |
|
| Known for | |
| Awards | Fellow of the Royal Society |
| Scientific career | |
| Fields | Mathematics |
| Institutions | Trinity College, Cambridge |
| Thesis | Highly Composite Numbers (1916) |
| Academic advisors | |
| Influences | G. S. Carr |
| Influenced | G. H. Hardy |
| Signature | |
Srinivasa Ramanujan FRS (/ˈsrɪnɪvɑːs rɑːˈmɑːnʊdʒən/;[1] born Srinivasa Ramanujan Aiyangar, IPA: [sriːniʋaːsa ɾaːmaːnud͡ʑan ajːaŋgar]; 22 December 1887 – 26 April 1920)[2][3] was an Indian mathematician who lived during the British Rule in India. Though he had almost no formal training in pure mathematics, he made substantial contributions to mathematical analysis, number theory, infinite series, and continued fractions, including solutions to mathematical problems then considered unsolvable. Ramanujan initially developed his own mathematical research in isolation: according to Hans Eysenck: "He tried to interest the leading professional mathematicians in his work, but failed for the most part. What he had to show them was too novel, too unfamiliar, and additionally presented in unusual ways; they could not be bothered".[4] Seeking mathematicians who could better understand his work, in 1913 he began a postal correspondence with the English mathematician G. H. Hardy at the University of Cambridge, England. Recognizing Ramanujan's work as extraordinary, Hardy arranged for him to travel to Cambridge. In his notes, Hardy commented that Ramanujan had produced groundbreaking new theorems, including some that "defeated me completely; I had never seen anything in the least like them before",[5] and some recently proven but highly advanced results.
During his short life, Ramanujan independently compiled nearly 3,900 results (mostly identities and equations).[6] Many were completely novel; his original and highly unconventional results, such as the Ramanujan prime, the Ramanujan theta function, partition formulae and mock theta functions, have opened entire new areas of work and inspired a vast amount of further research.[7] Nearly all his claims have now been proven correct.[8] The Ramanujan Journal, a scientific journal, was established to publish work in all areas of mathematics influenced by Ramanujan,[9] and his notebooks—containing summaries of his published and unpublished results—have been analysed and studied for decades since his death as a source of new mathematical ideas. As late as 2012, researchers continued to discover that mere comments in his writings about "simple properties" and "similar outputs" for certain findings were themselves profound and subtle number theory results that remained unsuspected until nearly a century after his death.[10][11] He became one of the youngest Fellows of the Royal Society and only the second Indian member, and the first Indian to be elected a Fellow of Trinity College, Cambridge. Of his original letters, Hardy stated that a single look was enough to show they could have been written only by a mathematician of the highest calibre, comparing Ramanujan to mathematical geniuses such as Euler and Jacobi.
In 1919, ill health—now believed to have been hepatic amoebiasis (a complication from episodes of dysentery many years previously)—compelled Ramanujan's return to India, where he died in 1920 at the age of 32. His last letters to Hardy, written in January 1920, show that he was still continuing to produce new mathematical ideas and theorems. His "lost notebook", containing discoveries from the last year of his life, caused great excitement among mathematicians when it was rediscovered in 1976.
A deeply religious Hindu,[12] Ramanujan credited his substantial mathematical capacities to divinity, and said the mathematical knowledge he displayed was revealed to him by his family goddess Namagiri Thayar. He once said, "An equation for me has no meaning unless it expresses a thought of God."[13]
Early life
Ramanujan (literally, "younger brother of Rama", a Hindu deity[14]:12) was born on 22 December 1887 into a Tamil Brahmin Iyengar family in Erode, Madras Presidency (now Tamil Nadu, India), at the residence of his maternal grandparents.[14]:11 His father, Kuppuswamy Srinivasa Iyengar, originally from Thanjavur district, worked as a clerk in a sari shop.[14]:17–18[15] His mother, Komalatammal, was a housewife and sang at a local temple.[16] They lived in a small traditional home on Sarangapani Sannidhi Street in the town of Kumbakonam.[17] The family home is now a museum. When Ramanujan was a year and a half old, his mother gave birth to a son, Sadagopan, who died less than three months later. In December 1889 Ramanujan contracted smallpox, but recovered, unlike the 4,000 others who died in a bad year in the Thanjavur district around this time. He moved with his mother to her parents' house in Kanchipuram, near Madras (now Chennai). His mother gave birth to two more children, in 1891 and 1894, both of whom died before their first birthdays.[14]:12
On 1 October 1892 Ramanujan was enrolled at the local school.[14]:13 After his maternal grandfather lost his job as a court official in Kanchipuram,[14]:19 Ramanujan and his mother moved back to Kumbakonam and he was enrolled in Kangayan Primary School.[14]:14 When his paternal grandfather died, he was sent back to his maternal grandparents, then living in Madras. He did not like school in Madras, and tried to avoid attending. His family enlisted a local constable to make sure he attended school. Within six months, Ramanujan was back in Kumbakonam.[14]:14
Since Ramanujan's father was at work most of the day, his mother took care of the boy, and they had a close relationship. From her he learned about tradition and puranas, to sing religious songs, to attend pujas at the temple, and to maintain particular eating habits—all part of Brahmin culture.[14]:20 At Kangayan Primary School Ramanujan performed well. Just before turning 10, in November 1897, he passed his primary examinations in English, Tamil, geography and arithmetic with the best scores in the district.[14]:25 That year Ramanujan entered Town Higher Secondary School, where he encountered formal mathematics for the first time.[14]:25
A child prodigy by age 11, he had exhausted the mathematical knowledge of two college students who were lodgers at his home. He was later lent a book written by S. L. Loney on advanced trigonometry.[18][19] He mastered this by the age of 13 while discovering sophisticated theorems on his own. By 14 he received merit certificates and academic awards that continued throughout his school career, and he assisted the school in the logistics of assigning its 1,200 students (each with differing needs) to its approximately 35 teachers.[14]:27 He completed mathematical exams in half the allotted time, and showed a familiarity with geometry and infinite series. Ramanujan was shown how to solve cubic equations in 1902; he developed his own method to solve the quartic. The following year he tried to solve the quintic, not knowing that it could not be solved by radicals.
In 1903, when he was 16, Ramanujan obtained from a friend a library copy of A Synopsis of Elementary Results in Pure and Applied Mathematics, G. S. Carr's collection of 5,000 theorems.[14]:39[20] Ramanujan reportedly studied the contents of the book in detail.[21] The book is generally acknowledged as a key element in awakening his genius.[21] The next year Ramanujan independently developed and investigated the Bernoulli numbers and calculated the Euler–Mascheroni constant up to 15 decimal places.[14]:90 His peers at the time said they "rarely understood him" and "stood in respectful awe" of him.[14]:27
When he graduated from Town Higher Secondary School in 1904, Ramanujan was awarded the K. Ranganatha Rao prize for mathematics by the school's headmaster, Krishnaswami Iyer. Iyer introduced Ramanujan as an outstanding student who deserved scores higher than the maximum.[14] He received a scholarship to study at Government Arts College, Kumbakonam,[14]:28[14]:45 but was so intent on mathematics that he could not focus on any other subjects and failed most of them, losing his scholarship in the process.[14]:47 In August 1905 Ramanujan ran away from home, heading towards Visakhapatnam, and stayed in Rajahmundry[22] for about a month.[14]:47–48 He later enrolled at Pachaiyappa's College in Madras. There he passed in mathematics, choosing only to attempt questions that appealed to him and leaving the rest unanswered, but performed poorly in other subjects, such as English, physiology and Sanskrit.[23] Ramanujan failed his Fellow of Arts exam in December 1906 and again a year later. Without an FA degree, he left college and continued to pursue independent research in mathematics, living in extreme poverty and often on the brink of starvation.[14]:55–56
In 1910, after a meeting between the 23-year-old Ramanujan and the founder of the Indian Mathematical Society, V. Ramaswamy Aiyer, Ramanujan began to get recognition in Madras's mathematical circles, leading to his inclusion as a researcher at the University of Madras.[24]
Adulthood in India
On 14 July 1909, Ramanujan married Janaki (Janakiammal; 21 March 1899 – 13 April 1994),[25] a girl his mother had selected for him a year earlier and who was ten years old when they married.[14]:71[26][27] It was not unusual then for marriages to be arranged with girls at a young age. Janaki was from Rajendram, a village close to Marudur (Karur district) Railway Station. Ramanujan's father did not participate in the marriage ceremony.[28] As was common at that time, Janaki continued to stay at her maternal home for three years after marriage, until she reached puberty. In 1912, she and Ramanujan's mother joined Ramanujan in Madras.[29]
After the marriage, Ramanujan developed a hydrocele testis.[14]:72 The condition could be treated with a routine surgical operation that would release the blocked fluid in the scrotal sac, but his family could not afford the operation. In January 1910, a doctor volunteered to do the surgery at no cost.[30]
After his successful surgery, Ramanujan searched for a job. He stayed at a friend's house while he went from door to door around Madras looking for a clerical position. To make money, he tutored students at Presidency College who were preparing for their F.A.[clarification needed] exam.[14]:73
In late 1910, Ramanujan was sick again. He feared for his health, and told his friend R. Radakrishna Iyer to "hand [his notebooks] over to Professor Singaravelu Mudaliar [the mathematics professor at Pachaiyappa's College] or to the British professor Edward B. Ross, of the Madras Christian College."[14]:74–75 After Ramanujan recovered and retrieved his notebooks from Iyer, he took a train from Kumbakonam to Villupuram, a city under French control.[31][32] In 1912, Ramanujan moved with his wife and mother to a house in Saiva Muthaiah Mudali street, George Town, Madras, where they lived for a few months.[33] In May 1913, upon securing a research position at Madras University, Ramanujan moved with his family to Triplicane.[34]
Pursuit of career in mathematics
In 1910, Ramanujan met deputy collector V. Ramaswamy Aiyer, who founded the Indian Mathematical Society.[14]:77 Wishing for a job at the revenue department where Aiyer worked, Ramanujan showed him his mathematics notebooks. As Aiyer later recalled:
I was struck by the extraordinary mathematical results contained in [the notebooks]. I had no mind to smother his genius by an appointment in the lowest rungs of the revenue department.[35]
Aiyer sent Ramanujan, with letters of introduction, to his mathematician friends in Madras.[14]:77 Some of them looked at his work and gave him letters of introduction to R. Ramachandra Rao, the district collector for Nellore and the secretary of the Indian Mathematical Society.[36][37][38] Rao was impressed by Ramanujan's research but doubted that it was his own work. Ramanujan mentioned a correspondence he had with Professor Saldhana, a notable Bombay mathematician, in which Saldhana expressed a lack of understanding of his work but concluded that he was not a fraud.[14]:80 Ramanujan's friend C. V. Rajagopalachari tried to quell Rao's doubts about Ramanujan's academic integrity. Rao agreed to give him another chance, and listened as Ramanujan discussed elliptic integrals, hypergeometric series, and his theory of divergent series, which Rao said ultimately convinced him of Ramanujan's brilliance.[14]:80 When Rao asked him what he wanted, Ramanujan replied that he needed work and financial support. Rao consented and sent him to Madras. He continued his research with Rao's financial aid. With Aiyer's help, Ramanujan had his work published in the Journal of the Indian Mathematical Society.[14]:86
One of the first problems he posed in the journal was to find the value of:[14]
He waited for a solution to be offered in three issues, over six months, but failed to receive any. At the end, Ramanujan supplied the solution to the problem himself. On page 105 of his first notebook, he formulated an equation that could be used to solve the infinitely nested radicals problem.
Using this equation, the answer to the question posed in the Journal was simply 3, obtained by setting x = 2, n = 1, and a = 0.[14]:87 Ramanujan wrote his first formal paper for the Journal on the properties of Bernoulli numbers. One property he discovered was that the denominators (sequence A027642 in the OEIS) of the fractions of Bernoulli numbers are always divisible by six. He also devised a method of calculating Bn based on previous Bernoulli numbers. One of these methods follows:
It will be observed that if n is even but not equal to zero,
- Bn is a fraction and the numerator of Bn/n in its lowest terms is a prime number,
- the denominator of Bn contains each of the factors 2 and 3 once and only once,
- 2n(2n − 1)Bn/n is an integer and 2(2n − 1)Bn consequently is an odd integer.
In his 17-page paper "Some Properties of Bernoulli's Numbers" (1911), Ramanujan gave three proofs, two corollaries and three conjectures.[14]:91 His writing initially had many flaws. As Journal editor M. T. Narayana Iyengar noted:
Mr. Ramanujan's methods were so terse and novel and his presentation so lacking in clearness and precision, that the ordinary [mathematical reader], unaccustomed to such intellectual gymnastics, could hardly follow him.[39]
Ramanujan later wrote another paper and also continued to provide problems in the Journal.[40] In early 1912, he got a temporary job in the Madras Accountant General's office, with a monthly salary of 20 rupees. He lasted only a few weeks.[41] Toward the end of that assignment, he applied for a position under the Chief Accountant of the Madras Port Trust.
In a letter dated 9 February 1912, Ramanujan wrote:
Sir,
I understand there is a clerkship vacant in your office, and I beg to apply for the same. I have passed the Matriculation Examination and studied up to the F.A. but was prevented from pursuing my studies further owing to several untoward circumstances. I have, however, been devoting all my time to Mathematics and developing the subject. I can say I am quite confident I can do justice to my work if I am appointed to the post. I therefore beg to request that you will be good enough to confer the appointment on me.[42]
Attached to his application was a recommendation from E. W. Middlemast, a mathematics professor at the Presidency College, who wrote that Ramanujan was "a young man of quite exceptional capacity in Mathematics".[43] Three weeks after he applied, on 1 March, Ramanujan learned that he had been accepted as a Class III, Grade IV accounting clerk, making 30 rupees per month.[14]:96 At his office Ramanujan easily and quickly completed the work he was given and spent his spare time doing mathematical research. Ramanujan's boss, Sir Francis Spring, and S. Narayana Iyer, a colleague who was also treasurer of the Indian Mathematical Society, encouraged Ramanujan in his mathematical pursuits.[citation needed]
Contacting British mathematicians
In the spring of 1913, Narayana Iyer, Ramachandra Rao and E. W. Middlemast tried to present Ramanujan's work to British mathematicians. M. J. M. Hill of University College London commented that Ramanujan's papers were riddled with holes.[14]:105 He said that although Ramanujan had "a taste for mathematics, and some ability", he lacked the necessary educational background and foundation to be accepted by mathematicians.[44] Although Hill did not offer to take Ramanujan on as a student, he gave thorough and serious professional advice on his work. With the help of friends, Ramanujan drafted letters to leading mathematicians at Cambridge University.[14]:106
The first two professors, H. F. Baker and E. W. Hobson, returned Ramanujan's papers without comment.[14]:170–171 On 16 January 1913, Ramanujan wrote to G. H. Hardy.[45] Coming from an unknown mathematician, the nine pages of mathematics made Hardy initially view Ramanujan's manuscripts as a possible fraud.[46] Hardy recognised some of Ramanujan's formulae but others "seemed scarcely possible to believe".[47]:494 One of the theorems Hardy found amazing was on the bottom of page three (valid for 0 < a < b + 1/2):
Hardy was also impressed by some of Ramanujan's other work relating to infinite series:
The first result had already been determined by G. Bauer in 1859. The second was new to Hardy, and was derived from a class of functions called hypergeometric series, which had first been researched by Euler and Gauss. Hardy found these results "much more intriguing" than Gauss's work on integrals.[14]:167 After seeing Ramanujan's theorems on continued fractions on the last page of the manuscripts, Hardy said the theorems "defeated me completely; I had never seen anything in the least like them before",[14]:168 and that they "must be true, because, if they were not true, no one would have the imagination to invent them".[14]:168 Hardy asked a colleague, J. E. Littlewood, to take a look at the papers. Littlewood was amazed by Ramanujan's genius. After discussing the papers with Littlewood, Hardy concluded that the letters were "certainly the most remarkable I have received" and that Ramanujan was "a mathematician of the highest quality, a man of altogether exceptional originality and power".[47]:494–495 One colleague, E. H. Neville, later remarked that "not one [theorem] could have been set in the most advanced mathematical examination in the world".[40]
On 8 February 1913 Hardy wrote Ramanujan a letter expressing interest in his work, adding that it was "essential that I should see proofs of some of your assertions".[48] Before his letter arrived in Madras during the third week of February, Hardy contacted the Indian Office to plan for Ramanujan's trip to Cambridge. Secretary Arthur Davies of the Advisory Committee for Indian Students met with Ramanujan to discuss the overseas trip.[49] In accordance with his Brahmin upbringing, Ramanujan refused to leave his country to "go to a foreign land".[14]:185 Meanwhile, he sent Hardy a letter packed with theorems, writing, "I have found a friend in you who views my labour sympathetically."[50]
To supplement Hardy's endorsement, Gilbert Walker, a former mathematical lecturer at Trinity College, Cambridge, looked at Ramanujan's work and expressed amazement, urging the young man to spend time at Cambridge.[14]:175 As a result of Walker's endorsement, B. Hanumantha Rao, a mathematics professor at an engineering college, invited Ramanujan's colleague Narayana Iyer to a meeting of the Board of Studies in Mathematics to discuss "what we can do for S. Ramanujan".[51] The board agreed to grant Ramanujan a monthly research scholarship of 75 rupees for the next two years at the University of Madras.[52] While he was engaged as a research student, Ramanujan continued to submit papers to the Journal of the Indian Mathematical Society. In one instance Iyer submitted some of Ramanujan's theorems on summation of series to the journal, adding, "The following theorem is due to S. Ramanujan, the mathematics student of Madras University." Later in November, British Professor Edward B. Ross of Madras Christian College, whom Ramanujan had met a few years before, stormed into his class one day with his eyes glowing, asking his students, "Does Ramanujan know Polish?" The reason was that in one paper, Ramanujan had anticipated the work of a Polish mathematician whose paper had just arrived in the day's mail.[53] In his quarterly papers Ramanujan drew up theorems to make definite integrals more easily solvable. Working off Giuliano Frullani's 1821 integral theorem, Ramanujan formulated generalisations that could be made to evaluate formerly unyielding integrals.[14]:183
Hardy's correspondence with Ramanujan soured after Ramanujan refused to come to England. Hardy enlisted a colleague lecturing in Madras, E. H. Neville, to mentor and bring Ramanujan to England.[14]:184 Neville asked Ramanujan why he would not go to Cambridge. Ramanujan apparently had now accepted the proposal; Neville said, "Ramanujan needed no converting" and "his parents' opposition had been withdrawn".[40] Apparently Ramanujan's mother had a vivid dream in which the family goddess, the deity of Namagiri, commanded her "to stand no longer between her son and the fulfilment of his life's purpose".[40] On March 17, 1914 Ramanujan traveled to England by ship[54] leaving his wife to stay with his parents in India.[citation needed]
Life in England
Ramanujan departed from Madras aboard the S.S. Nevasa on 17 March 1914.[14]:196 When he disembarked in London on 14 April, Neville was waiting for him with a car. Four days later, Neville took him to his house on Chesterton Road in Cambridge. Ramanujan immediately began his work with Littlewood and Hardy. After six weeks Ramanujan moved out of Neville's house and took up residence on Whewell's Court, a five-minute walk from Hardy's room.[14]:202 Hardy and Littlewood began to look at Ramanujan's notebooks. Hardy had already received 120 theorems from Ramanujan in the first two letters, but there were many more results and theorems in the notebooks. Hardy saw that some were wrong, others had already been discovered, and the rest were new breakthroughs.[55] Ramanujan left a deep impression on Hardy and Littlewood. Littlewood commented, "I can believe that he's at least a Jacobi",[56] while Hardy said he "can compare him only with Euler or Jacobi."[57]
Ramanujan spent nearly five years in Cambridge collaborating with Hardy and Littlewood, and published part of his findings there. Hardy and Ramanujan had highly contrasting personalities. Their collaboration was a clash of different cultures, beliefs, and working styles. In the previous few decades the foundations of mathematics had come into question and the need for mathematically rigorous proofs recognised. Hardy was an atheist and an apostle of proof and mathematical rigour, whereas Ramanujan was a deeply religious man who relied very strongly on his intuition and insights. Hardy tried his best to fill the gaps in Ramanujan's education and to mentor him in the need for formal proofs to support his results, without hindering his inspiration—a conflict that neither found easy.
Ramanujan was awarded a Bachelor of Arts by Research degree[58][59] (the predecessor of the PhD degree) in March 1916 for his work on highly composite numbers, sections of the first part of which had been published the preceding year in the Proceedings of the London Mathematical Society. The paper was more than 50 pages long and proved various properties of such numbers. Hardy disliked this topic area but remarked that though it engaged with what he called the 'backwater of mathematics', in it Ramanujan displayed 'extraordinary mastery over the algebra of inequalities'.[60] On 6 December 1917, Ramanujan was elected to the London Mathematical Society. On 2 May 1918, he was elected a Fellow of the Royal Society,[61] the second Indian admitted, after Ardaseer Cursetjee in 1841. At age 31 Ramanujan was one of the youngest Fellows in the Royal Society's history. He was elected "for his investigation in elliptic functions and the Theory of Numbers." On 13 October 1918 he was the first Indian to be elected a Fellow of Trinity College, Cambridge.[14]:299–300
Illness and death
Ramanujan was plagued by health problems throughout his life. His health worsened in England; possibly he was also less resilient due to the difficulty of keeping to the strict dietary requirements of his religion there and because of wartime rationing in 1914–18. He was diagnosed with tuberculosis and a severe vitamin deficiency, and confined to a sanatorium. In 1919 he returned to Kumbakonam, Madras Presidency, and in 1920 he died at the age of 32. After his death his brother Tirunarayanan compiled Ramanujan's remaining handwritten notes, consisting of formulae on singular moduli, hypergeometric series and continued fractions.[29]
Ramanujan's widow, Smt. Janaki Ammal, moved to Bombay; in 1931 she returned to Madras and settled in Triplicane, where she supported herself on a pension from Madras University and income from tailoring. In 1950 she adopted a son, W. Narayanan, who eventually became an officer of the State Bank of India and raised a family. In her later years she was granted a lifetime pension from Ramanujan's former employer, the Madras Port Trust, and pensions from, among others, the Indian National Science Academy and the state governments of Tamil Nadu, Andhra Pradesh and West Bengal. She continued to cherish Ramanujan's memory, and was active in efforts to increase his public recognition; prominent mathematicians, including George Andrews, Bruce C. Berndt and Béla Bollobás made it a point to visit her while in India. She died at her Triplicane residence in 1994.[28][29]
A 1994 analysis of Ramanujan's medical records and symptoms by Dr. D. A. B. Young[62] concluded that his medical symptoms—including his past relapses, fevers, and hepatic conditions—were much closer to those resulting from hepatic amoebiasis, an illness then widespread in Madras, than tuberculosis. He had two episodes of dysentery before he left India. When not properly treated, amoebic dysentery can lie dormant for years and lead to hepatic amoebiasis, whose diagnosis was not then well established.[63] At the time, if properly diagnosed, amoebiasis was a treatable and often curable disease;[63][64] British soldiers who contracted it during the First World War were being successfully cured of amoebiasis around the time Ramanujan left England.[65]
Personality and spiritual life
Ramanujan has been described as a person of a somewhat shy and quiet disposition, a dignified man with pleasant manners.[66] He lived a simple life at Cambridge.[14]:234,241 Ramanujan's first Indian biographers describe him as a rigorously orthodox Hindu. He credited his acumen to his family goddess, Namagiri Thayar (Goddess Mahalakshmi) of Namakkal. He looked to her for inspiration in his work[14]:36 and said he dreamed of blood drops that symbolised her consort, Narasimha. Later he had visions of scrolls of complex mathematical content unfolding before his eyes.[14]:281 He often said, "An equation for me has no meaning unless it expresses a thought of God."[67]
Hardy cites Ramanujan as remarking that all religions seemed equally true to him.[14]:283 Hardy further argued that Ramanujan's religious belief had been romanticised by Westerners and overstated—in reference to his belief, not practice—by Indian biographers. At the same time, he remarked on Ramanujan's strict vegetarianism.[68]
Mathematical achievements
In mathematics there is a distinction between insight and formulating or working through a proof. Ramanujan proposed an abundance of formulae that could be investigated later in depth. G. H. Hardy said that Ramanujan's discoveries are unusually rich and that there is often more to them than initially meets the eye. As a byproduct of his work, new directions of research were opened up. Examples of the most intriguing of these formulae include infinite series for π, one of which is given below:
This result is based on the negative fundamental discriminant d = −4 × 58 = −232 with class number h(d) = 2. Further, 26390 = 5 × 7 × 13 × 58 and 16 × 9801 = 3962, which is related to the fact that
This might be compared to Heegner numbers, which have class number 1 and yield similar formulae.
Ramanujan's series for π converges extraordinarily rapidly and forms the basis of some of the fastest algorithms currently used to calculate π. Truncating the sum to the first term also gives the approximation 9801√2/4412 for π, which is correct to six decimal places; truncating it to the first two terms gives a value correct to 14 decimal places. See also the more general Ramanujan–Sato series.
One of Ramanujan's remarkable capabilities was the rapid solution of problems, illustrated by the following anecdote about an incident in which P. C. Mahalanobis posed a problem:
Imagine that you are on a street with houses marked 1 through n. There is a house in between (x) such that the sum of the house numbers to the left of it equals the sum of the house numbers to its right. If n is between 50 and 500, what are n and x?' This is a bivariate problem with multiple solutions. Ramanujan thought about it and gave the answer with a twist: He gave a continued fraction. The unusual part was that it was the solution to the whole class of problems. Mahalanobis was astounded and asked how he did it. 'It is simple. The minute I heard the problem, I knew that the answer was a continued fraction. Which continued fraction, I asked myself. Then the answer came to my mind', Ramanujan replied."[69][70]
His intuition also led him to derive some previously unknown identities, such as
for all θ such that 

In 1918 Hardy and Ramanujan studied the partition function P(n) extensively. They gave a non-convergent asymptotic series that permits exact computation of the number of partitions of an integer. In 1937 Hans Rademacher refined their formula to find an exact convergent series solution to this problem. Ramanujan and Hardy's work in this area gave rise to a powerful new method for finding asymptotic formulae called the circle method.[71]
In the last year of his life, Ramanujan discovered mock theta functions.[72] For many years these functions were a mystery, but they are now known to be the holomorphic parts of harmonic weak Maass forms.
The Ramanujan conjecture
Although there are numerous statements that could have borne the name Ramanujan conjecture, one was highly influential on later work. In particular, the connection of this conjecture with conjectures of André Weil in algebraic geometry opened up new areas of research. That Ramanujan conjecture is an assertion on the size of the tau-function, which has as generating function the discriminant modular form Δ(q), a typical cusp form in the theory of modular forms. It was finally proven in 1973, as a consequence of Pierre Deligne's proof of the Weil conjectures. The reduction step involved is complicated. Deligne won a Fields Medal in 1978 for that work.[7]
In his paper "On certain arithmetical functions", Ramanujan defined the so-called delta-function, whose coefficients are called τ(n) (the Ramanujan tau function).[73] He proved many congruences for these numbers, such as τ(p) ≡ 1 + p11 mod 691 for primes p. This congruence (and others like it that Ramanujan proved) inspired Jean-Pierre Serre (1954 Fields Medalist) to conjecture that there is a theory of Galois representations that "explains" these congruences and more generally all modular forms. Δ(z) is the first example of a modular form to be studied in this way. Deligne (in his Fields Medal-winning work) proved Serre's conjecture. The proof of Fermat's Last Theorem proceeds by first reinterpreting elliptic curves and modular forms in terms of these Galois representations. Without this theory there would be no proof of Fermat's Last Theorem.[74]
Ramanujan's notebooks
While still in Madras, Ramanujan recorded the bulk of his results in four notebooks of looseleaf paper. They were mostly written up without any derivations. This is probably the origin of the misapprehension that Ramanujan was unable to prove his results and simply thought up the final result directly. Mathematician Bruce C. Berndt, in his review of these notebooks and Ramanujan's work, says that Ramanujan most certainly was able to prove most of his results, but chose not to.
This may have been for any number of reasons. Since paper was very expensive, Ramanujan would do most of his work and perhaps his proofs on slate, and then transfer just the results to paper. Using a slate was common for mathematics students in the Madras Presidency at the time. He was also quite likely to have been influenced by the style of G. S. Carr's book, which stated results without proofs. Finally, it is possible that Ramanujan considered his work to be for his personal interest alone and therefore recorded only the results.[75]
The first notebook has 351 pages with 16 somewhat organised chapters and some unorganised material. The second has 256 pages in 21 chapters and 100 unorganised pages, and the third 33 unorganised pages. The results in his notebooks inspired numerous papers by later mathematicians trying to prove what he had found. Hardy himself wrote papers exploring material from Ramanujan's work, as did G. N. Watson, B. M. Wilson, and Bruce Berndt.[75] In 1976, George Andrews rediscovered a fourth notebook with 87 unorganised pages, the so-called "lost notebook".[63]
Hardy–Ramanujan number 1729
The number 1729 is known as the Hardy–Ramanujan number after a famous visit by Hardy to see Ramanujan at a hospital. In Hardy's words:[76]
I remember once going to see him when he was ill at Putney. I had ridden in taxi cab number 1729 and remarked that the number seemed to me rather a dull one, and that I hoped it was not an unfavorable omen. "No", he replied, "it is a very interesting number; it is the smallest number expressible as the sum of two cubes in two different ways."
Immediately before this anecdote, Hardy quoted Littlewood as saying, "Every positive integer was one of [Ramanujan's] personal friends."[77]
The two different ways are:
Generalisations of this idea have created the notion of "taxicab numbers".
Mathematicians' views of Ramanujan
In his obituary of Ramanujan, written for Nature in 1920, Hardy observed that Ramanujan's work primarily involved fields less known even among other pure mathematicians, concluding:
His insight into formulae was quite amazing, and altogether beyond anything I have met with in any European mathematician. It is perhaps useless to speculate as to his history had he been introduced to modern ideas and methods at sixteen instead of at twenty-six. It is not extravagant to suppose that he might have become the greatest mathematician of his time. What he actually did is wonderful enough… when the researches which his work has suggested have been completed, it will probably seem a good deal more wonderful than it does to-day.[47]
Hardy further said:[78]
He combined a power of generalisation, a feeling for form, and a capacity for rapid modification of his hypotheses, that were often really startling, and made him, in his own peculiar field, without a rival in his day. The limitations of his knowledge were as startling as its profundity. Here was a man who could work out modular equations and theorems... to orders unheard of, whose mastery of continued fractions was... beyond that of any mathematician in the world, who had found for himself the functional equation of the zeta function and the dominant terms of many of the most famous problems in the analytic theory of numbers; and yet he had never heard of a doubly periodic function or of Cauchy's theorem, and had indeed but the vaguest idea of what a function of a complex variable was..."
When asked about the methods Ramanujan employed to arrive at his solutions, Hardy said they were "arrived at by a process of mingled argument, intuition, and induction, of which he was entirely unable to give any coherent account."[79] He also said that he had "never met his equal, and can compare him only with Euler or Jacobi".[79]
K. Srinivasa Rao has said,[80] "As for his place in the world of Mathematics, we quote Bruce C. Berndt: 'Paul Erdős has passed on to us Hardy's personal ratings of mathematicians. Suppose that we rate mathematicians on the basis of pure talent on a scale from 0 to 100. Hardy gave himself a score of 25, J. E. Littlewood 30, David Hilbert 80 and Ramanujan 100.'" During a May 2011 lecture at IIT Madras, Berndt said that over the last 40 years, as nearly all of Ramanujan's conjectures have been proven, there had been greater appreciation of Ramanujan's work and brilliance, and that Ramanujan's work was now pervading many areas of modern mathematics and physics.[72][81]
Posthumous recognition
The year after his death, Nature listed Ramanujan among other distinguished scientists and mathematicians on a "Calendar of Scientific Pioneers" who had achieved eminence.[82] Ramanujan's home state of Tamil Nadu celebrates 22 December (Ramanujan's birthday) as 'State IT Day'. Stamps picturing Ramanujan were issued by the government of India in 1962, 2011, 2012 and 2016.[83]
Since Ramanujan's centennial year, his birthday, 22 December, has been annually celebrated as Ramanujan Day by the Government Arts College, Kumbakonam, where he studied, and at the IIT Madras in Chennai. The International Centre for Theoretical Physics (ICTP) has created a prize in Ramanujan's name for young mathematicians from developing countries in cooperation with the International Mathematical Union, which nominates members of the prize committee. SASTRA University, a private university based in Tamil Nadu, has instituted the SASTRA Ramanujan Prize of US$10,000 to be given annually to a mathematician not exceeding age 32 for outstanding contributions in an area of mathematics influenced by Ramanujan. Based on the recommendations of a committee appointed by the University Grants Commission (UGC), Government of India, the Srinivasa Ramanujan Centre, established by SASTRA, has been declared an off-campus centre under the ambit of SASTRA University. House of Ramanujan Mathematics, a museum of Ramanujan's life and work, is also on this campus. SASTRA purchased and renovated the house where Ramanujan lived at Kumabakonam.[84]
In 2011, on the 125th anniversary of his birth, the Indian government declared that 22 December will be celebrated every year as National Mathematics Day.[85] Then Indian Prime Minister Manmohan Singh also declared that 2012 would be celebrated as National Mathematics Year.[86]
Ramanujan IT City is an information technology (IT) special economic zone (SEZ) in Chennai that was built in 2011. Situated next to the Tidel Park, it includes 25 acres (10 ha) with two zones, with a total area of 5.7 million square feet (530,000 m2), including 4.5 million square feet (420,000 m2) of office space.[87]
In popular culture
- The Man Who Knew Infinity is a 2015 film based on Kanigel's book. British actor Dev Patel portrays Ramanujan.[88][89][90]
- Ramanujan, an Indo-British collaboration film chronicling Ramanujan's life, was released in 2014 by the independent film company Camphor Cinema.[91] The cast and crew include director Gnana Rajasekaran, cinematographer Sunny Joseph and editor B. Lenin.[92][93] Indian and English stars Abhinay Vaddi, Suhasini Maniratnam, Bhama, Kevin McGowan and Michael Lieber star in pivotal roles.[94]
- Nandan Kudhyadi directed the Indian documentary films The Genius of Srinivasa Ramanujan (2013) and Srinivasa Ramanujan: The Mathematician And His Legacy (2016) about the mathematician.[95]
- Ramanujan (The Man Who Reshaped 20th Century Mathematics), an Indian docudrama film directed by Akashdeep released in 2018.[96]
- M. N. Krish's thriller novel The Steradian Trail weaves Ramanujan and his accidental discovery into its plot connecting religion, mathematics, finance and economics.[97][98]
- Partition, a play by Ira Hauptman about Hardy and Ramanujan, was first performed in 2013.[99][100][101][102]
- The play First Class Man by Alter Ego Productions[103] was based on David Freeman's First Class Man. The play centres around Ramanujan and his complex and dysfunctional relationship with Hardy. On 16 October 2011 it was announced that Roger Spottiswoode, best known for his James Bond film Tomorrow Never Dies, is working on the film version, starring Siddharth.[104]
- A Disappearing Number is a British stage production by the company Complicite that explores the relationship between Hardy and Ramanujan.[105]
- David Leavitt's novel The Indian Clerk explores the events following Ramanujan's letter to Hardy.[106][107]
- Google honoured Ramanujan on his 125th birth anniversary by replacing its logo with a doodle on its home page.[108][109]
- Ramanujan was mentioned in the 1997 film Good Will Hunting, in a scene where professor Gerald Lambeau (Stellan Skarsgård) explains to Sean Maguire (Robin Williams) the genius of Will Hunting (Matt Damon) by comparing him to Ramanujan.[110]
- The brilliant mathematician Amita Ramanujan on the tv show Numb3rs, played by half-Indian actress Navi Rawat, is named for Ramanujan.[citation needed]
Further works of Ramanujan's mathematics
- George E. Andrews and Bruce C. Berndt, Ramanujan's Lost Notebook: Part I (Springer, 2005, ISBN 0-387-25529-X)[111]
- George E. Andrews and Bruce C. Berndt, Ramanujan's Lost Notebook: Part II, (Springer, 2008, ISBN 978-0-387-77765-8)
- George E. Andrews and Bruce C. Berndt, Ramanujan's Lost Notebook: Part III, (Springer, 2012, ISBN 978-1-4614-3809-0)
- George E. Andrews and Bruce C. Berndt, Ramanujan's Lost Notebook: Part IV, (Springer, 2013, ISBN 978-1-4614-4080-2)
- George E. Andrews and Bruce C. Berndt, Ramanujan's Lost Notebook: Part V, (Springer, 2018, ISBN 978-3-319-77832-7)
- M. P. Chaudhary, A simple solution of some integrals given by Srinivasa Ramanujan, (Resonance: J. Sci. Education – publication of Indian Academy of Science, 2008)[112]
- M.P. Chaudhary, Mock theta functions to mock theta conjectures, SCIENTIA, Series A : Math. Sci., (22)(2012) 33–46.
- M.P. Chaudhary, On modular relations for the Roger-Ramanujan type identities, Pacific J. Appl. Math., 7(3)(2016) 177–184.
Selected publications on Ramanujan and his work
- Berndt, Bruce C. (1998). Butzer, P. L.; Oberschelp, W.; Jongen, H. Th. (eds.). Charlemagne and His Heritage: 1200 Years of Civilization and Science in Europe (PDF). Turnhout, Belgium: Brepols Verlag. pp. 119–146. ISBN 978-2-503-50673-9.
- Berndt, Bruce C.; Rankin, Robert A. (1995). Ramanujan: Letters and Commentary. 9. Providence, Rhode Island: American Mathematical Society. ISBN 978-0-8218-0287-8.
- Berndt, Bruce C.; Rankin, Robert A. (2001). Ramanujan: Essays and Surveys. 22. Providence, Rhode Island: American Mathematical Society. ISBN 978-0-8218-2624-9.
- Berndt, Bruce C. (2006). Number Theory in the Spirit of Ramanujan. 9. Providence, Rhode Island: American Mathematical Society. ISBN 978-0-8218-4178-5.
- Berndt, Bruce C. (1985). Ramanujan's Notebooks. Part I. New York: Springer. ISBN 978-0-387-96110-1.
- Berndt, Bruce C. (1999). Ramanujan's Notebooks. Part II. New York: Springer. ISBN 978-0-387-96794-3.
- Berndt, Bruce C. (2004). Ramanujan's Notebooks. Part III. New York: Springer. ISBN 978-0-387-97503-0.
- Berndt, Bruce C. (1993). Ramanujan's Notebooks. Part IV. New York: Springer. ISBN 978-0-387-94109-7.
- Berndt, Bruce C. (2005). Ramanujan's Notebooks. Part V. New York: Springer. ISBN 978-0-387-94941-3.
- Hardy, G. H. (March 1937). "The Indian Mathematician Ramanujan". The American Mathematical Monthly. 44 (3): 137–155. doi:10.2307/2301659. JSTOR 2301659.
- Hardy, G. H. (1978). Ramanujan. New York: Chelsea Pub. Co. ISBN 978-0-8284-0136-4.
- Hardy, G. H. (1999). Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work. Providence, Rhode Island: American Mathematical Society. ISBN 978-0-8218-2023-0.
- Henderson, Harry (1995). Modern Mathematicians. New York: Facts on File Inc. ISBN 978-0-8160-3235-8.
- Kanigel, Robert (1991). The Man Who Knew Infinity: a Life of the Genius Ramanujan. New York: Charles Scribner's Sons. ISBN 978-0-684-19259-8.
- Leavitt, David (2007). The Indian Clerk (paperback ed.). London: Bloomsbury. ISBN 978-0-7475-9370-6.
- Narlikar, Jayant V. (2003). Scientific Edge: the Indian Scientist From Vedic to Modern Times. New Delhi, India: Penguin Books. ISBN 978-0-14-303028-7.
- Ono, Ken; Aczel, Amir D. (13 April 2016). My Search for Ramanujan: How I Learned to Count. Springer. ISBN 978-3319255668.
- Sankaran, T. M. (2005). "Srinivasa Ramanujan- Ganitha lokathile Mahaprathibha" (in Malayalam). Kochi, India: Kerala Sastra Sahithya Parishath.
Selected publications on works of Ramanujan
- Ramanujan, Srinivasa; Hardy, G. H.; Seshu Aiyar, P. V.; Wilson, B. M.; Berndt, Bruce C. (2000). Collected Papers of Srinivasa Ramanujan. AMS. ISBN 978-0-8218-2076-6.
- This book was originally published in 1927[113] after Ramanujan's death. It contains the 37 papers published in professional journals by Ramanujan during his lifetime. The third reprint contains additional commentary by Bruce C. Berndt.
- S. Ramanujan (1957). Notebooks (2 Volumes). Bombay: Tata Institute of Fundamental Research.
- These books contain photocopies of the original notebooks as written by Ramanujan.
- S. Ramanujan (1988). The Lost Notebook and Other Unpublished Papers. New Delhi: Narosa. ISBN 978-3-540-18726-4.
- This book contains photo copies of the pages of the "Lost Notebook".
- Problems posed by Ramanujan, Journal of the Indian Mathematical Society.
- S. Ramanujan (2012). Notebooks (2 Volumes). Bombay: Tata Institute of Fundamental Research.
- This was produced from scanned and microfilmed images of the original manuscripts by expert archivists of Roja Muthiah Research Library, Chennai.
See also
References
- Bell, E. T. (1928). "Collected Papers of Srinivasa Ramanujan, edited by G. H. Hardy, P. V. Seshu Aiyar and B. M. Wilson". Bull. Amer. Math. Soc. 34 (6): 783–784. doi:10.1090/S0002-9904-1928-04651-7.
External links
Media links
- Biswas, Soutik (16 March 2006). "Film to celebrate mathematics genius". BBC. Retrieved 24 August 2006.
- Feature Film on Mathematics Genius Ramanujan by Dev Benegal and Stephen Fry
- BBC radio programme about Ramanujan – episode 5
- A biographical song about Ramanujan's life
Biographical links
- Srinivasa Ramanujan at the Mathematics Genealogy Project
- O'Connor, John J.; Robertson, Edmund F., "Srinivasa Ramanujan", MacTutor History of Mathematics archive, University of St Andrews
- Weisstein, Eric Wolfgang (ed.). "Ramanujan, Srinivasa (1887–1920)". ScienceWorld.
- A short biography of Ramanujan
- "Our Devoted Site for Great Mathematical Genius"
Other links
- Wolfram, Stephen (27 April 2016). "Who Was Ramanujan?".
- A Study Group For Mathematics: Srinivasa Ramanujan Iyengar
- The Ramanujan Journal – An international journal devoted to Ramanujan
- International Math Union Prizes, including a Ramanujan Prize
- Hindu.com: Norwegian and Indian mathematical geniuses, Ramanujan – Essays and Surveys, Ramanujan's growing influence, Ramanujan's mentor
- Hindu.com: The sponsor of Ramanujan
- Bruce C. Berndt; Robert A. Rankin (2000). "The Books Studied by Ramanujan in India". American Mathematical Monthly. 107 (7): 595–601. doi:10.2307/2589114. JSTOR 2589114. MR 1786233.
- "Ramanujan's mock theta function puzzle solved"
- Ramanujan's papers and notebooks
- Sample page from the second notebook
- Ramanujan on Fried Eye
- Clark, Alex. "163 and Ramanujan Constant". Numberphile. Brady Haran. Archived from the original on 4 February 2018. Retrieved 23 June 2018.
- Srinivasa Ramanujan
- 1887 births
- 1920 deaths
- Scientists from Tamil Nadu
- 20th-century Indian mathematicians
- Indian Hindus
- Mental calculators
- Indian combinatorialists
- Indian number theorists
- Fellows of Trinity College, Cambridge
- Fellows of the Royal Society
- Pi
- People from Erode district
- University of Madras alumni
- People from Thanjavur district
- 19th-century Indian mathematicians
- Number theorists
- Infectious disease deaths in India
Languages
ideas that were critical to the proof of Fermat's last theorem
|title= (help)
Leonardo da Vinci
Leonardo da Vinci | |
|---|---|
 This portrait attributed to Francesco Melzi, c. 1515–1518, is the only certain contemporary depiction of Leonardo.[1][2] | |
| Born | Leonardo di ser Piero da Vinci 15 April 1452 |
| Died | 2 May 1519 (aged 67) |
| Education | Studio of Andrea del Verrocchio |
| Known for |
|
Notable work |
|
| Movement | High Renaissance |
| Signature | |
 | |
Leonardo da Vinci[b] (15 April 1452 – 2 May 1519) was an Italian polymath of the High Renaissance who was active as a painter, draughtsman, engineer, scientist, theorist, sculptor and architect.[3] While his fame initially rested on his achievements as a painter, he also became known for his notebooks, in which he made drawings and notes on a variety of subjects, including anatomy, astronomy, botany, cartography, painting, and paleontology. Leonardo's genius epitomized the Renaissance humanist ideal,[4] and his collective works compose a contribution to later generations of artists matched only by that of his younger contemporary, Michelangelo.[3][4]
Born out of wedlock to a successful notary and a lower-class woman in, or near, Vinci, he was educated in Florence by the renowned Italian painter and sculptor Andrea del Verrocchio. He began his career in the city, but then spent much time in the service of Ludovico Sforza in Milan. Later, he worked in Florence and Milan again, as well as briefly in Rome, all while attracting a large following of imitators and students. Upon the invitation of Francis I, he spent his last three years in France, where he died in 1519. Since his death, there has not been a time where his achievements, diverse interests, personal life, and empirical thinking have failed to incite interest and admiration,[3][4] making him a frequent namesake and subject in culture.
Leonardo is among the greatest painters in the history of art and is often credited as the founder of the High Renaissance.[3] Despite having many lost works and less than 25 attributed major works—including numerous unfinished works—he created some of the most influential paintings in Western art.[3] His magnum opus, the Mona Lisa, is his best known work and often regarded as the world's most famous painting. The Last Supper is the most reproduced religious painting of all time and his Vitruvian Man drawing is also regarded as a cultural icon. In 2017, Salvator Mundi, attributed in whole or part to Leonardo,[5] was sold at auction for US$450.3 million, setting a new record for most expensive painting ever sold at public auction.
Revered for his technological ingenuity, he conceptualized flying machines, a type of armored fighting vehicle, concentrated solar power, an adding machine,[6] and the double hull. Relatively few of his designs were constructed or even feasible during his lifetime, as the modern scientific approaches to metallurgy and engineering were only in their infancy during the Renaissance. Some of his smaller inventions, however, entered the world of manufacturing unheralded, such as an automated bobbin winder and a machine for testing the tensile strength of wire. He made substantial discoveries in anatomy, civil engineering, geology, optics, tribology, and hydrodynamics, but he did not publish his findings and they had little to no direct influence on subsequent science.[7]
Biography
Early life (1452–1472)
Birth and background
Leonardo da Vinci,[b] properly named Leonardo di ser Piero da Vinci (Leonardo, son of ser Piero from Vinci),[8][9][c] was born on 15 April 1452 in, or close to, the Tuscan hill town of Vinci; Florence was 20 miles away.[10][11][d] He was born out of wedlock to Ser Piero da Vinci (Ser Piero di Antonio di Ser Piero di Ser Guido da Vinci; 1426–1504),[15] a Florentine legal notary,[10] and Caterina (c. 1434 – 1494), from the lower-class.[16][17] It remains uncertain where Leonardo was born; the traditional account, from a local oral tradition recorded by the historian Emanuele Repetti,[18] is that he was born in Anchiano, a country hamlet that would have offered sufficient privacy for the illegitimate birth, though, it is still possible he was born in a house in Florence, which Ser Piero almost certainly had.[19][a] Leonardo's parents both married separately the year after his birth. Caterina—who later appears in Leonardo's notes as only "Caterina" or "Catelina"—is usually identified as the Caterina Buti del Vacca who married the local artisan Antonio di Piero Buti del Vacca, nicknamed "L'Accattabriga" ("the quarrelsome one").[16][18] Other theories have been proposed, particularly that of art historian Martin Kemp, who suggested Caterina di Meo Lippi, an orphan that married supposably with aid from Ser Piero and his family.[20][e][f] Ser Piero married Albiera Amadori—having been betrothed to her the previous year—and after her death in 1462, went on to have three subsequent marriages.[18][23][g] From all the marriages, Leonardo eventually had 12 half-siblings, who were much younger than he was (the last was born when Leonardo was 40 years old) and with whom he had very little contact.[h]
Very little is known about Leonardo's childhood and much is shrouded in myth, partially because of his biography in the frequently apocryphal Lives of the Most Excellent Painters, Sculptors, and Architects (1550) from the 16th-century art historian Giorgio Vasari.[26][27] Tax records indicate that by at least 1457 he lived in the household of his paternal grandfather, Antonio da Vinci,[10] but it is possible that he spent the years before then in the care of his mother in Vinci, either Anchiano or Campo Zeppi in the parish of San Pantaleone.[28][29] He is thought to have been close with his uncle, Francesco da Vinci,[3] but his father was likely in Florence most of the time.[10] Ser Piero, who was the descendant of a long line of notaries, established an official residence in Florence by at least 1469 and led a successful career.[10] Despite his family history, Leonardo only received a basic and informal education in (vernacular) writing, reading and math, possibly because his artistic talents were recognized early, so his family decided to focus their attention there.[10]
Later in life, Leonardo recorded his earliest memory, now in the Codex Atlanticus.[30] While writing on the flight of birds, he recalled as an infant when a kite came to his cradle and opened his mouth with its tail; commentators still debate whether the anecdote was an actual memory or a fantasy.[31][i]
Verrocchio's workshop
In the mid-1460s, Leonardo's family moved to Florence, which at the time was the centre of Christian Humanist thought and culture.[32] Around the age of 14,[24] he became a garzone (studio boy) in the workshop of Andrea del Verrocchio, who was the leading Florentine painter and sculptor of his time.[32] This was about the time of the death of Verrocchio's master, the great sculptor Donatello.[j] Leonardo became an apprentice by the age of 17 and remained in training for seven years.[34] Other famous painters apprenticed in the workshop or associated with it include Ghirlandaio, Perugino, Botticelli, and Lorenzo di Credi.[35][36] Leonardo was exposed to both theoretical training and a wide range of technical skills,[37] including drafting, chemistry, metallurgy, metal working, plaster casting, leather working, mechanics, and wood-work, as well as the artistic skills of drawing, painting, sculpting, and modelling.[38][k]
Leonardo was a contemporary of Botticelli, Ghirlandaio and Perugino, who were all slightly older than he was.[39] He would have met them at the workshop of Verrocchio or at the Platonic Academy of the Medici.[35] Florence was ornamented by the works of artists such as Donatello's contemporaries Masaccio, whose figurative frescoes were imbued with realism and emotion, and Ghiberti, whose Gates of Paradise, gleaming with gold leaf, displayed the art of combining complex figure compositions with detailed architectural backgrounds. Piero della Francesca had made a detailed study of perspective,[40] and was the first painter to make a scientific study of light. These studies and Leon Battista Alberti's treatise De pictura were to have a profound effect on younger artists and in particular on Leonardo's own observations and artworks.[33][41]
Much of the painting in Verrocchio's workshop was done by his assistants. According to Vasari, Leonardo collaborated with Verrocchio on his The Baptism of Christ, painting the young angel holding Jesus' robe in a manner that was so far superior to his master's that Verrocchio put down his brush and never painted again, although this is believed to be an apocryphal story.[‡ 1] Close examination reveals areas of the work that have been painted or touched-up over the tempera, using the new technique of oil paint, including the landscape, the rocks seen through the brown mountain stream, and much of the figure of Jesus, bearing witness to the hand of Leonardo.[42] Leonardo may have been the model for two works by Verrocchio: the bronze statue of David in the Bargello, and the Archangel Raphael in Tobias and the Angel.[13]
Giorgio Vasari, the 16th-century biographer of Renaissance painters, tells a story of Leonardo as a very young man: A local peasant made himself a round shield and requested that Ser Piero have it painted for him. Leonardo, inspired by the story of Medusa, responded with a painting of a monster spitting fire that was so terrifying that his father bought a different shield to give to the peasant and sold Leonardo's to a Florentine art dealer for 100 ducats, who in turn sold it to the Duke of Milan.[‡ 2]
First Florentine period (1472–c. 1482)
By 1472, at the age of 20, Leonardo qualified as a master in the Guild of Saint Luke, the guild of artists and doctors of medicine,[l] but even after his father set him up in his own workshop, his attachment to Verrocchio was such that he continued to collaborate and live with him.[35][43] Leonardo's earliest known dated work is a 1473 pen-and-ink drawing of the Arno valley,[36] which has been cited as the first "pure" landscape in the Occident.[m][44] According to Vasari, the young Leonardo was the first to suggest making the Arno river a navigable channel between Florence and Pisa.[45]
In January 1478, Leonardo received an independent commission to paint an altarpiece for the Chapel of St. Bernard in the Palazzo Vecchio,[46] an indication of his independence from Verrocchio's studio. An anonymous early biographer, known as Anonimo Gaddiano, claims that in 1480 Leonardo was living with the Medici and often worked in the garden of the Piazza San Marco, Florence, where a Neoplatonic academy of artists, poets and philosophers organized by the Medici met.[13][n] In March 1481, he received a commission from the monks of San Donato in Scopeto for The Adoration of the Magi.[47] Neither of these initial commissions were completed, being abandoned when Leonardo went to offer his services to Duke of Milan Ludovico Sforza. Leonardo wrote Sforza a letter which described the diverse things that he could achieve in the fields of engineering and weapon design, and mentioned that he could paint.[36][48] He brought with him a silver string instrument—either a lute or lyre—in the form of a horse's head.[48]
With Alberti, Leonardo visited the home of the Medici and through them came to know the older Humanist philosophers of whom Marsiglio Ficino, proponent of Neoplatonism; Cristoforo Landino, writer of commentaries on Classical writings, and John Argyropoulos, teacher of Greek and translator of Aristotle were the foremost. Also associated with the Platonic Academy of the Medici was Leonardo's contemporary, the brilliant young poet and philosopher Pico della Mirandola.[39][41][49] In 1482, Leonardo was sent as an ambassador by Lorenzo de' Medici to Ludovico il Moro, who ruled Milan between 1479 and 1499.[39][13]
Madonna of the Carnation, c. 1472–1478, Alte Pinakothek, Munich
Landscape of the Arno Valley (1473), probably the first true landscape in art[44]
Ginevra de' Benci, c. 1474–1480, National Gallery of Art, Washington D.C.
Benois Madonna, c. 1478–1481, Hermitage, Saint Petersburg
Sketch of the hanging of Bernardo Bandini Baroncelli, 1479
First Milanese period (c. 1482–1499)
Leonardo worked in Milan from 1482 until 1499. He was commissioned to paint the Virgin of the Rocks for the Confraternity of the Immaculate Conception and The Last Supper for the monastery of Santa Maria delle Grazie.[50] In the spring of 1485, Leonardo travelled to Hungary on behalf of Sforza to meet king Matthias Corvinus, and was commissioned by him to paint a Madonna.[51] Leonardo was employed on many other projects for Sforza, including the preparation of floats and pageants for special occasions, a drawing and wooden model for a competition to design the cupola for Milan Cathedral (which he withdrew),[52] and a model for a huge equestrian monument to Ludovico's predecessor Francesco Sforza. This would have surpassed in size the only two large equestrian statues of the Renaissance, Donatello's Gattamelata in Padua and Verrocchio's Bartolomeo Colleoni in Venice, and became known as the Gran Cavallo.[36] Leonardo completed a model for the horse and made detailed plans for its casting,[36] but in November 1494, Ludovico gave the bronze to his brother-in-law to be used for a cannon to defend the city from Charles VIII of France.[36]
Salaì, or Il Salaino ("The Little Unclean One," i.e., the devil), entered Leonardo's household in 1490 as an assistant. After only a year, Leonardo made a list of his misdemeanours, calling him "a thief, a liar, stubborn, and a glutton," after he had made off with money and valuables on at least five occasions and spent a fortune on clothes.[53] Nevertheless, Leonardo treated him with great indulgence, and he remained in Leonardo's household for the next thirty years.[54] Salaì executed a number of paintings under the name of Andrea Salaì, but although Vasari claims that Leonardo "taught him a great deal about painting,"[‡ 3] his work is generally considered to be of less artistic merit than others among Leonardo's pupils, such as Marco d'Oggiono and Boltraffio.
Head of a Woman, c. 1483–1485, Royal Library of Turin
Portrait of a Musician, c. 1483–1487, Pinacoteca Ambrosiana, Milan
The Vitruvian Man (c. 1485) Accademia, Venice
Leonardo's horse in silverpoint, c. 1488[55]
La Belle Ferronnière, c. 1490–1498
Second Florentine period (1500–1508)
When Ludovico Sforza was overthrown by France in 1500, Leonardo fled Milan for Venice, accompanied by his assistant Salaì and friend, the mathematician Luca Pacioli.[56] In Venice, Leonardo was employed as a military architect and engineer, devising methods to defend the city from naval attack.[35] On his return to Florence in 1500, he and his household were guests of the Servite monks at the monastery of Santissima Annunziata and were provided with a workshop where, according to Vasari, Leonardo created the cartoon of The Virgin and Child with St Anne and St John the Baptist, a work that won such admiration that "men and women, young and old" flocked to see it "as if they were attending a great festival."[‡ 4][o]
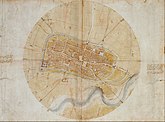
In Cesena in 1502, Leonardo entered the service of Cesare Borgia, the son of Pope Alexander VI, acting as a military architect and engineer and travelling throughout Italy with his patron.[56] Leonardo created a map of Cesare Borgia's stronghold, a town plan of Imola in order to win his patronage. Upon seeing it, Cesare hired Leonardo as his chief military engineer and architect. Later in the year, Leonardo produced another map for his patron, one of Chiana Valley, Tuscany, so as to give his patron a better overlay of the land and greater strategic position. He created this map in conjunction with his other project of constructing a dam from the sea to Florence, in order to allow a supply of water to sustain the canal during all seasons.
Leonardo had left Borgia's service and returned to Florence by early 1503,[58] where he rejoined the Guild of Saint Luke on 18 October of that year. By this same month, Leonardo had begun working on a portrait of Lisa del Giocondo, the model for the Mona Lisa,[59][60] which he would continue working on until his twilight years. In January 1504, he was part of a committee formed to recommend where Michelangelo's statue of David should be placed.[61] He then spent two years in Florence designing and painting a mural of The Battle of Anghiari for the Signoria,[56] with Michelangelo designing its companion piece, The Battle of Cascina.[p]
In 1506, Leonardo was summoned to Milan by Charles II d'Amboise, the acting French governor of the city.[64] There, Leonardo took on another pupil, Count Francesco Melzi, the son of a Lombard aristocrat, who is considered to have been his favourite student.[35] The Council of Florence wished Leonardo to return promptly to finish The Battle of Anghiari, but he was given leave at the behest of Louis XII, who considered commissioning the artist to make some portraits.[64] Leonardo may have commenced a project for an equestrian figure of d'Amboise;[65] a wax model survives and, if genuine, is the only extant example of Leonardo's sculpture. Leonardo was otherwise free to pursue his scientific interests.[64] Many of Leonardo's most prominent pupils either knew or worked with him in Milan,[35] including Bernardino Luini, Giovanni Antonio Boltraffio, and Marco d'Oggiono. In 1507, Leonardo was in Florence sorting out a dispute with his brothers over the estate of his father, who had died in 1504.
The Virgin and Child with Saint Anne, c. 1501–1519, Louvre, Paris
Leonardo's map of Imola, created for Cesare Borgia, 1502
Study for The Battle of Anghiari (now lost), c. 1503, Museum of Fine Arts, Budapest
La Scapigliata, c. 1506–1508 (unfinished), Galleria Nazionale di Parma, Parma
Study for Leda and the Swan (now lost), c. 1506-1508, Chatsworth House, England
Second Milanese period (1508–1513)
By 1508, Leonardo was back in Milan, living in his own house in Porta Orientale in the parish of Santa Babila.[66]
In 1512, Leonardo was working on plans for an equestrian monument for Gian Giacomo Trivulzio, but this was prevented by an invasion of a confederation of Swiss, Spanish and Venetian forces, which drove the French from Milan. Leonardo stayed in the city, spending several months in 1513 at the Medici's Vaprio d'Adda villa.[67]
Rome and France (1513–1519)
In March of 1513, Lorenzo de' Medici's son Giovanni assumed the papacy (as Leo X); Leonardo went to Rome that September, where he was received by the pope's brother Giuliano.[67] From September 1513 to 1516, Leonardo spent much of his time living in the Belvedere Courtyard in the Apostolic Palace, where Michelangelo and Raphael were both active.[66] Leonardo was given an allowance of 33 ducats a month, and according to Vasari, decorated a lizard with scales dipped in quicksilver.[68] The pope gave him a painting commission of unknown subject matter, but cancelled it when the artist set about developing a new kind of varnish.[68][q] Leonardo became ill, in what may have been the first of multiple strokes leading to his death.[68] He practiced botany in the Gardens of Vatican City, and was commissioned to make plans for the pope's proposed draining of the Pontine Marshes.[69] He also dissected cadavers, making notes for a treatise on vocal cords;[70] these he gave to an official in hopes of regaining the pope's favor, but was unsuccessful.[68]
In October 1515, King Francis I of France recaptured Milan.[47] Leonardo was present at the 19 December meeting of Francis I and Leo X, which took place in Bologna.[35][71][72] In 1516, Leonardo entered Francis' service, being given the use of the manor house Clos Lucé, near the king's residence at the royal Château d'Amboise. Being frequently visited by Francis, he drew plans for an immense castle town the king intended to erect at Romorantin, and made a mechanical lion, which during a pageant walked toward the king and—upon being struck by a wand—opened its chest to reveal a cluster of lilies.[73][‡ 3][r] Leonardo was accompanied during this time by his friend and apprentice Francesco Melzi, and supported by a pension totalling 10,000 scudi.[66] At some point, Melzi drew a portrait of Leonardo; the only others known from his lifetime were a sketch by an unknown assistant on the back of one of Leonardo's studies (c. 1517)[75] and a drawing by Giovanni Ambrogio Figino depicting an elderly Leonardo with his right arm assuaged by cloth.[76][s] The latter, in addition to the record of an October 1517 visit by Louis d'Aragon,[t] confirms an account of Leonardo's right hand being paralytic at the age of 65,[79] which may indicate why he left works such as the Mona Lisa unfinished.[77][80][81] He continued to work at some capacity until eventually becoming ill and bedridden for several months.[79]
Death
Leonardo died at Clos Lucé on 2 May 1519 at the age of 67, possibly of a stroke.[82][81][83] Francis I had become a close friend. Vasari describes Leonardo as lamenting on his deathbed, full of repentance, that "he had offended against God and men by failing to practice his art as he should have done."[84] Vasari states that in his last days, Leonardo sent for a priest to make his confession and to receive the Holy Sacrament.[‡ 5] Vasari also records that the king held Leonardo's head in his arms as he died, although this story may be legend rather than fact.[u][v] In accordance with his will, sixty beggars carrying tapers followed Leonardo's casket.[49][w] Melzi was the principal heir and executor, receiving, as well as money, Leonardo's paintings, tools, library and personal effects. Leonardo's other long-time pupil and companion, Salaì, and his servant Baptista de Vilanis, each received half of Leonardo's vineyards.[86] His brothers received land, and his serving woman received a fur-lined cloak. On 12 August 1519, Leonardo's remains were interred in the Collegiate Church of Saint Florentin at the Château d'Amboise.[87]
Salaì owned the Mona Lisa at the time of his death in 1524, and in his will it was assessed at 505 lire, an exceptionally high valuation for a small panel portrait.[88] Some 20 years after Leonardo's death, Francis was reported by the goldsmith and sculptor Benvenuto Cellini as saying: "There had never been another man born in the world who knew as much as Leonardo, not so much about painting, sculpture and architecture, as that he was a very great philosopher."[89]
Personal life
Despite the thousands of pages Leonardo left in notebooks and manuscripts, he scarcely made reference to his personal life.[2]
Within Leonardo's lifetime, his extraordinary powers of invention, his "outstanding physical beauty," "infinite grace," "great strength and generosity," "regal spirit and tremendous breadth of mind," as described by Vasari,[‡ 6] as well as all other aspects of his life, attracted the curiosity of others. One such aspect was his love for animals, likely including vegetarianism and according to Vasari, a habit of purchasing caged birds and releasing them.[90][‡ 7]
Leonardo had many friends who are now renowned either in their fields or for their historical significance. They included the mathematician Luca Pacioli,[91] with whom he collaborated on the book Divina proportione in the 1490s. Leonardo appears to have had no close relationships with women except for his friendship with Cecilia Gallerani and the two Este sisters, Beatrice and Isabella.[92] While on a journey that took him through Mantua, he drew a portrait of Isabella that appears to have been used to create a painted portrait, now lost.[35]
Beyond friendship, Leonardo kept his private life secret. His sexuality has been the subject of satire, analysis, and speculation. This trend began in the mid-16th century and was revived in the 19th and 20th centuries, most notably by Sigmund Freud in his Leonardo da Vinci, A Memory of His Childhood.[93] Leonardo's most intimate relationships were perhaps with his pupils Salaì and Melzi. Melzi, writing to inform Leonardo's brothers of his death, described Leonardo's feelings for his pupils as both loving and passionate. It has been claimed since the 16th century that these relationships were of a sexual or erotic nature. Court records of 1476, when he was aged twenty-four, show that Leonardo and three other young men were charged with sodomy in an incident involving a well-known male prostitute. The charges were dismissed for lack of evidence, and there is speculation that since one of the accused, Lionardo de Tornabuoni, was related to Lorenzo de' Medici, the family exerted its influence to secure the dismissal.[94] Since that date much has been written about his presumed homosexuality[95] and its role in his art, particularly in the androgyny and eroticism manifested in Saint John the Baptist and Bacchus and more explicitly in a number of erotic drawings.[96]
Paintings
Despite the recent awareness and admiration of Leonardo as a scientist and inventor, for the better part of four hundred years his fame rested on his achievements as a painter. A handful of works that are either authenticated or attributed to him have been regarded as among the great masterpieces. These paintings are famous for a variety of qualities that have been much imitated by students and discussed at great length by connoisseurs and critics. By the 1490s Leonardo had already been described as a "Divine" painter.[97]
Among the qualities that make Leonardo's work unique are his innovative techniques for laying on the paint; his detailed knowledge of anatomy, light, botany and geology; his interest in physiognomy and the way humans register emotion in expression and gesture; his innovative use of the human form in figurative composition; and his use of subtle gradation of tone. All these qualities come together in his most famous painted works, the Mona Lisa, the Last Supper, and the Virgin of the Rocks.[98]
Early works
Leonardo first gained attention for his work on the Baptism of Christ, painted in conjunction with Verrocchio. Two other paintings appear to date from his time at Verrocchio's workshop, both of which are Annunciations. One is small, 59 centimetres (23 in) long and 14 centimetres (5.5 in) high. It is a "predella" to go at the base of a larger composition, a painting by Lorenzo di Credi from which it has become separated. The other is a much larger work, 217 centimetres (85 in) long.[99] In both Annunciations, Leonardo used a formal arrangement, like two well-known pictures by Fra Angelico of the same subject, of the Virgin Mary sitting or kneeling to the right of the picture, approached from the left by an angel in profile, with a rich flowing garment, raised wings and bearing a lily. Although previously attributed to Ghirlandaio, the larger work is now generally attributed to Leonardo.[100]
In the smaller painting, Mary averts her eyes and folds her hands in a gesture that symbolised submission to God's will. Mary is not submissive, however, in the larger piece. The girl, interrupted in her reading by this unexpected messenger, puts a finger in her bible to mark the place and raises her hand in a formal gesture of greeting or surprise.[33] This calm young woman appears to accept her role as the Mother of God, not with resignation but with confidence. In this painting, the young Leonardo presents the humanist face of the Virgin Mary, recognising humanity's role in God's incarnation.
Paintings of the 1480s
In the 1480s, Leonardo received two very important commissions and commenced another work that was of ground-breaking importance in terms of composition. Two of the three were never finished, and the third took so long that it was subject to lengthy negotiations over completion and payment.
One of these paintings was Saint Jerome in the Wilderness, which Bortolon associates with a difficult period of Leonardo's life, as evidenced in his diary: "I thought I was learning to live; I was only learning to die."[35] Although the painting is barely begun, the composition can be seen and is very unusual.[x] Jerome, as a penitent, occupies the middle of the picture, set on a slight diagonal and viewed somewhat from above. His kneeling form takes on a trapezoid shape, with one arm stretched to the outer edge of the painting and his gaze looking in the opposite direction. J. Wasserman points out the link between this painting and Leonardo's anatomical studies.[101] Across the foreground sprawls his symbol, a great lion whose body and tail make a double spiral across the base of the picture space. The other remarkable feature is the sketchy landscape of craggy rocks against which the figure is silhouetted.
The daring display of figure composition, the landscape elements and personal drama also appear in the great unfinished masterpiece, the Adoration of the Magi, a commission from the Monks of San Donato a Scopeto. It is a complex composition, of about 250 x 250 centimetres. Leonardo did numerous drawings and preparatory studies, including a detailed one in linear perspective of the ruined classical architecture that forms part of the background. In 1482 Leonardo went to Milan at the behest of Lorenzo de' Medici in order to win favour with Ludovico il Moro, and the painting was abandoned.[13]
The third important work of this period is the Virgin of the Rocks, commissioned in Milan for the Confraternity of the Immaculate Conception. The painting, to be done with the assistance of the de Predis brothers, was to fill a large complex altarpiece.[102] Leonardo chose to paint an apocryphal moment of the infancy of Christ when the infant John the Baptist, in protection of an angel, met the Holy Family on the road to Egypt. The painting demonstrates an eerie beauty as the graceful figures kneel in adoration around the infant Christ in a wild landscape of tumbling rock and whirling water.[103] While the painting is quite large, about 200×120 centimetres, it is not nearly as complex as the painting ordered by the monks of St Donato, having only four figures rather than about fifty and a rocky landscape rather than architectural details. The painting was eventually finished; in fact, two versions of the painting were finished: one remained at the chapel of the Confraternity, while Leonardo took the other to France. The Brothers did not get their painting, however, nor the de Predis their payment, until the next century.[36][56]
Leonardo's most remarkable portrait of this period is the Lady with an Ermine, presumed to be Cecilia Gallerani (c. 1483–1490), lover of Ludovico Sforza.[104][105] The painting is characterised by the pose of the figure with the head turned at a very different angle to the torso, unusual at a date when many portraits were still rigidly in profile. The ermine plainly carries symbolic meaning, relating either to the sitter, or to Ludovico who belonged to the prestigious Order of the Ermine.[104]
Paintings of the 1490s
Leonardo's most famous painting of the 1490s is The Last Supper, commissioned for the refectory of the Convent of Santa Maria della Grazie in Milan. It represents the last meal shared by Jesus with his disciples before his capture and death, and shows the moment when Jesus has just said "one of you will betray me", and the consternation that this statement caused.[36]
The writer Matteo Bandello observed Leonardo at work and wrote that some days he would paint from dawn till dusk without stopping to eat and then not paint for three or four days at a time.[106] This was beyond the comprehension of the prior of the convent, who hounded him until Leonardo asked Ludovico to intervene. Vasari describes how Leonardo, troubled over his ability to adequately depict the faces of Christ and the traitor Judas, told the Duke that he might be obliged to use the prior as his model.[‡ 8]
When finished, the painting was acclaimed as a masterpiece of design and characterization,[‡ 9] but it deteriorated rapidly, so that within a hundred years it was described by one viewer as "completely ruined."[107] Leonardo, instead of using the reliable technique of fresco, had used tempera over a ground that was mainly gesso, resulting in a surface subject to mould and to flaking.[108] Despite this, the painting remains one of the most reproduced works of art; countless copies have been made in various mediums.
It is recorded that in 1492, Leonardo, with assistants painted the Sala delle Asse in the Sforza Castle in Milan, with a trompe-l'œil depicting trees, with an intricate labyrinth of leaves and knots on the ceiling.[109]
Paintings of the 16th century
In 1505 Leonardo was commissioned to paint The Battle of Anghiari in the Salone dei Cinquecento (Hall of the Five Hundred) in the Palazzo Vecchio, Florence. Leonardo devised a dynamic composition depicting four men riding raging war horses engaged in a battle for possession of a standard, at the Battle of Anghiari in 1440. Michelangelo was assigned the opposite wall to depict the Battle of Cascina. Leonardo's painting deteriorated rapidly and is now known from a copy by Rubens.[110]
Among the works created by Leonardo in the 16th century is the small portrait known as the Mona Lisa or La Gioconda, the laughing one. In the present era, it is arguably the most famous painting in the world. Its fame rests, in particular, on the elusive smile on the woman's face, its mysterious quality perhaps due to the subtly shadowed corners of the mouth and eyes such that the exact nature of the smile cannot be determined. The shadowy quality for which the work is renowned came to be called "sfumato," or Leonardo's smoke. Vasari, who is generally thought to have known the painting only by repute, said that "the smile was so pleasing that it seemed divine rather than human; and those who saw it were amazed to find that it was as alive as the original."[‡ 10][y]
Other characteristics of the painting are the unadorned dress, in which the eyes and hands have no competition from other details; the dramatic landscape background, in which the world seems to be in a state of flux; the subdued colouring; and the extremely smooth nature of the painterly technique, employing oils laid on much like tempera, and blended on the surface so that the brushstrokes are indistinguishable.[z] Vasari expressed the opinion that the manner of painting would make even "the most confident master...despair and lose heart."[‡ 11] The perfect state of preservation and the fact that there is no sign of repair or overpainting is rare in a panel painting of this date.[113]
In the painting Virgin and Child with St. Anne, the composition again picks up the theme of figures in a landscape, which Wasserman describes as "breathtakingly beautiful"[114] and harkens back to the St Jerome picture with the figure set at an oblique angle. What makes this painting unusual is that there are two obliquely set figures superimposed. Mary is seated on the knee of her mother, St Anne. She leans forward to restrain the Christ Child as he plays roughly with a lamb, the sign of his own impending sacrifice.[36] This painting, which was copied many times, influenced Michelangelo, Raphael, and Andrea del Sarto,[115] and through them Pontormo and Correggio. The trends in composition were adopted in particular by the Venetian painters Tintoretto and Veronese.
Drawings
Leonardo was a prolific draughtsman, keeping journals full of small sketches and detailed drawings recording all manner of things that took his attention. As well as the journals there exist many studies for paintings, some of which can be identified as preparatory to particular works such as The Adoration of the Magi, The Virgin of the Rocks and The Last Supper.[116] His earliest dated drawing is a Landscape of the Arno Valley, 1473, which shows the river, the mountains, Montelupo Castle and the farmlands beyond it in great detail.[35][116][aa] According to art historian Ludwig Heydenreich, this is "The first true landscape in art."[117] Massimo Polidoro says that it was the first landscape "not to be the background of some religious scene or a portrait. It is the first [documented] time where a landscape was drawn just for the sake of it."[44]
Among his famous drawings are the Vitruvian Man, a study of the proportions of the human body; the Head of an Angel, for The Virgin of the Rocks in the Louvre; a botanical study of Star of Bethlehem; and a large drawing (160×100 cm) in black chalk on coloured paper of The Virgin and Child with St. Anne and St. John the Baptist in the National Gallery, London.[116] This drawing employs the subtle sfumato technique of shading, in the manner of the Mona Lisa. It is thought that Leonardo never made a painting from it, the closest similarity being to The Virgin and Child with St. Anne in the Louvre.[118]
Other drawings of interest include numerous studies generally referred to as "caricatures" because, although exaggerated, they appear to be based upon observation of live models. Vasari relates that if Leonardo saw a person with an interesting face he would follow them around all day observing them.[‡ 12] There are numerous studies of beautiful young men, often associated with Salaì, with the rare and much admired facial feature, the so-called "Grecian profile."[ab] These faces are often contrasted with that of a warrior.[116] Salaì is often depicted in fancy-dress costume. Leonardo is known to have designed sets for pageants with which these may be associated. Other, often meticulous, drawings show studies of drapery. A marked development in Leonardo's ability to draw drapery occurred in his early works. Another often-reproduced drawing is a macabre sketch that was done by Leonardo in Florence in 1479 showing the body of Bernardo Baroncelli, hanged in connection with the murder of Giuliano, brother of Lorenzo de' Medici, in the Pazzi conspiracy.[116] In his notes, Leonardo recorded the colours of the robes that Baroncelli was wearing when he died.
Like the two contemporary architects Donato Bramante (who designed the Belvedere Courtyard) and Antonio da Sangallo the Elder, Leonardo experimented with designs for centrally planned churches, a number of which appear in his journals, as both plans and views, although none was ever realised.[39][119]
Journals and notes
Renaissance humanism recognised no mutually exclusive polarities between the sciences and the arts, and Leonardo's studies in science and engineering are sometimes considered as impressive and innovative as his artistic work.[36] These studies were recorded in 13,000 pages of notes and drawings, which fuse art and natural philosophy (the forerunner of modern science). They were made and maintained daily throughout Leonardo's life and travels, as he made continual observations of the world around him.[36] Leonardo's notes and drawings display an enormous range of interests and preoccupations, some as mundane as lists of groceries and people who owed him money and some as intriguing as designs for wings and shoes for walking on water. There are compositions for paintings, studies of details and drapery, studies of faces and emotions, of animals, babies, dissections, plant studies, rock formations, whirlpools, war machines, flying machines and architecture.[36]
These notebooks—originally loose papers of different types and sizes, were largely entrusted to Leonardo's pupil and heir Francesco Melzi after the master's death.[120] These were to be published, a task of overwhelming difficulty because of its scope and Leonardo's idiosyncratic writing.[121] Some of Leonardo's drawings were copied by an anonymous Milanese artist for a planned treatise on art c. 1570.[122] After Melzi's death in 1570, the collection passed to his son, the lawyer Orazio, who initially took little interest in the journals.[120] In 1587, a Melzi household tutor named Lelio Gavardi took 13 of the manuscripts to Pisa; there, the architect Giovanni Magenta reproached Gavardi for having taken the manuscripts illicitly and returned them to Orazio. Having many more such works in his possession, Orazio gifted the volumes to Magenta. News spread of these lost works of Leonardo's, and Orazio retrieved seven of the 13 manuscripts, which he then gave to Pompeo Leoni for publication in two volumes; one of these was the Codex Atlanticus. The other six works had been distributed to a few others.[123] After Orazio's death, his heirs sold the rest of Leonardo's possessions, and thus began their dispersal.[124]
Some works have found their way into major collections such as the Royal Library at Windsor Castle, the Louvre, the Biblioteca Nacional de España, the Victoria and Albert Museum, the Biblioteca Ambrosiana in Milan, which holds the 12-volume Codex Atlanticus, and the British Library in London, which has put a selection from the Codex Arundel (BL Arundel MS 263) online.[125] Works have also been at Holkham Hall, the Metropolitan Museum of Art, and in the private hands of John Nicholas Brown I and Robert Lehman.[120] The Codex Leicester is the only privately owned major scientific work of Leonardo; it is owned by Bill Gates and displayed once a year in different cities around the world.
Most of Leonardo's writings are in mirror-image cursive.[126][44] Since Leonardo wrote with his left hand, it was probably easier for him to write from right to left.[127][ac] Leonardo used a variety of shorthand and symbols, and states in his notes that he intended to prepare them for publication.[126] In many cases a single topic is covered in detail in both words and pictures on a single sheet, together conveying information that would not be lost if the pages were published out of order.[130] Why they were not published during Leonardo's lifetime is unknown.[36]
Science and inventions
Leonardo's approach to science was observational: he tried to understand a phenomenon by describing and depicting it in utmost detail and did not emphasise experiments or theoretical explanation. Since he lacked formal education in Latin and mathematics, contemporary scholars mostly ignored Leonardo the scientist, although he did teach himself Latin. His keen observations in many areas were noted, such as when he wrote "Il sole non si move." ("The Sun does not move.")[131]
In the 1490s he studied mathematics under Luca Pacioli and prepared a series of drawings of regular solids in a skeletal form to be engraved as plates for Pacioli's book Divina proportione, published in 1509.[36] While living in Milan, he studied light from the summit of Monte Rosa.[64] Scientific writings in his notebook on fossils have been considered as influential on early palaeontology.[132]
The content of his journals suggest that he was planning a series of treatises on a variety of subjects. A coherent treatise on anatomy is said to have been observed during a visit by Cardinal Louis d'Aragon's secretary in 1517.[133] Aspects of his work on the studies of anatomy, light and the landscape were assembled for publication by Melzi and eventually published as A Treatise on Painting in France and Italy in 1651 and Germany in 1724,[134] with engravings based upon drawings by the Classical painter Nicolas Poussin.[4] According to Arasse, the treatise, which in France went into 62 editions in fifty years, caused Leonardo to be seen as "the precursor of French academic thought on art."[36]
While Leonardo's experimentation followed scientific methods, a recent and exhaustive analysis of Leonardo as a scientist by Fritjof Capra argues that Leonardo was a fundamentally different kind of scientist from Galileo, Newton and other scientists who followed him in that, as a "Renaissance Man", his theorising and hypothesising integrated the arts and particularly painting.[135][page needed]
Anatomy and physiology
Leonardo started his study in the anatomy of the human body under the apprenticeship of Verrocchio, who demanded that his students develop a deep knowledge of the subject.[136] As an artist, he quickly became master of topographic anatomy, drawing many studies of muscles, tendons and other visible anatomical features.
As a successful artist, Leonardo was given permission to dissect human corpses at the Hospital of Santa Maria Nuova in Florence and later at hospitals in Milan and Rome. From 1510 to 1511 he collaborated in his studies with the doctor Marcantonio della Torre. Leonardo made over 240 detailed drawings and wrote about 13,000 words towards a treatise on anatomy.[137] Only a small amount of the material on anatomy was published in Leonardo's Treatise on painting.[121] During the time that Melzi was ordering the material into chapters for publication, they were examined by a number of anatomists and artists, including Vasari, Cellini and Albrecht Dürer, who made a number of drawings from them.[121]
Leonardo's anatomical drawings include many studies of the human skeleton and its parts, and of muscles and sinews. He studied the mechanical functions of the skeleton and the muscular forces that are applied to it in a manner that prefigured the modern science of biomechanics.[138] He drew the heart and vascular system, the sex organs and other internal organs, making one of the first scientific drawings of a fetus in utero.[116] The drawings and notation are far ahead of their time, and if published would undoubtedly have made a major contribution to medical science.[137]
Leonardo also closely observed and recorded the effects of age and of human emotion on the physiology, studying in particular the effects of rage. He drew many figures who had significant facial deformities or signs of illness.[36][116] Leonardo also studied and drew the anatomy of many animals, dissecting cows, birds, monkeys, bears, and frogs, and comparing in his drawings their anatomical structure with that of humans. He also made a number of studies of horses.[116]
Leonardo's dissections and documentation of muscles, nerves, and vessels helped to describe the physiology and mechanics of movement. He attempted to identify the source of 'emotions' and their expression. He found it difficult to incorporate the prevailing system and theories of bodily humours, but eventually he abandoned these physiological explanations of bodily functions. He made the observations that humours were not located in cerebral spaces or ventricles. He documented that the humours were not contained in the heart or the liver, and that it was the heart that defined the circulatory system. He was the first to define atherosclerosis and liver cirrhosis. He created models of the cerebral ventricles with the use of melted wax and constructed a glass aorta to observe the circulation of blood through the aortic valve by using water and grass seed to watch flow patterns. Vesalius published his work on anatomy and physiology in De humani corporis fabrica in 1543.[139]
Engineering and inventions
During his lifetime, Leonardo was also valued as an engineer. With the same rational and analytical approach that moved him to represent the human body and to investigate anatomy, Leonardo studied and designed many machines and devices. He drew their “anatomy” with unparalleled mastery, producing the first form of the modern technical drawing, including a perfected "exploded view" technique, to represent internal components. Those studies and projects collected in his codices fill more than 5,000 pages.[140] In a letter of 1482 to the lord of Milan Ludovico il Moro, he wrote that he could create all sorts of machines both for the protection of a city and for siege. When he fled from Milan to Venice in 1499, he found employment as an engineer and devised a system of moveable barricades to protect the city from attack. In 1502, he created a scheme for diverting the flow of the Arno river, a project on which Niccolò Machiavelli also worked.[141][142] He continued to contemplate the canalization of Lombardy's plains while in Louis XII's company[64] and of the Loire and its tributaries in the company of Francis I.[143] Leonardo's journals include a vast number of inventions, both practical and impractical. They include musical instruments, a mechanical knight, hydraulic pumps, reversible crank mechanisms, finned mortar shells, and a steam cannon.[35][36]
Leonardo was fascinated by the phenomenon of flight for much of his life, producing many studies, including Codex on the Flight of Birds (c. 1505), as well as plans for several flying machines, such as a flapping ornithopter and a machine with a helical rotor.[36] A 2003 documentary by British television station Channel Four, titled Leonardo's Dream Machines, various designs by Leonardo, such as a parachute and a giant crossbow, were interpreted and constructed.[144][145] Some of those designs proved successful, whilst others fared less well when tested.
Research performed by Marc van den Broek revealed older prototypes for more than 100 inventions that are ascribed to Leonardo. Similarities between Leonardo's illustrations and drawings from the Middle Ages and from Ancient Greece and Rome, the Chinese and Persian Empires, and Egypt suggest that a large portion of Leonardo's inventions had been conceived before his lifetime. Leonardo's innovation was to combine different functions from existing drafts and set them into scenes that illustrated their utility. By reconstituting technical inventions he created something new.[146]
In his notebooks, Leonardo first stated the ‘laws’ of sliding friction in 1493.[147] His inspiration for investigating friction came about in part from his study of perpetual motion, which he correctly concluded was not possible.[148] His results were never published and the friction laws were not rediscovered until 1699 by Guillaume Amontons, with whose name they are now usually associated.[147] For this contribution, Leonardo was named as the first of the 23 "Men of Tribology" by Duncan Dowson.[149]
Legacy
Leonardo's fame within his own lifetime was such that the King of France carried him away like a trophy, and was claimed to have supported him in his old age and held him in his arms as he died. Interest in Leonardo and his work has never diminished. Crowds still queue to see his best-known artworks, T-shirts still bear his most famous drawing, and writers continue to hail him as a genius while speculating about his private life, as well as about what one so intelligent actually believed in.[36]
The continued admiration that Leonardo commanded from painters, critics and historians is reflected in many other written tributes. Baldassare Castiglione, author of Il Cortegiano (The Courtier), wrote in 1528: "...Another of the greatest painters in this world looks down on this art in which he is unequalled..."[150] while the biographer known as "Anonimo Gaddiano" wrote, c. 1540: "His genius was so rare and universal that it can be said that nature worked a miracle on his behalf..."[151] Vasari, in the enlarged edition of Lives of the Artists (1568)[‡ 13] introduced his chapter on Leonardo with the following words:
In the normal course of events many men and women are born with remarkable talents; but occasionally, in a way that transcends nature, a single person is marvellously endowed by Heaven with beauty, grace and talent in such abundance that he leaves other men far behind, all his actions seem inspired and indeed everything he does clearly comes from God rather than from human skill. Everyone acknowledged that this was true of Leonardo da Vinci, an artist of outstanding physical beauty, who displayed infinite grace in everything that he did and who cultivated his genius so brilliantly that all problems he studied he solved with ease.
The 19th century brought a particular admiration for Leonardo's genius, causing Henry Fuseli to write in 1801: "Such was the dawn of modern art, when Leonardo da Vinci broke forth with a splendour that distanced former excellence: made up of all the elements that constitute the essence of genius..."[152] This is echoed by A.E. Rio who wrote in 1861: "He towered above all other artists through the strength and the nobility of his talents."[153]
By the 19th century, the scope of Leonardo's notebooks was known, as well as his paintings. Hippolyte Taine wrote in 1866: "There may not be in the world an example of another genius so universal, so incapable of fulfilment, so full of yearning for the infinite, so naturally refined, so far ahead of his own century and the following centuries."[154] Art historian Bernard Berenson wrote in 1896: "Leonardo is the one artist of whom it may be said with perfect literalness: Nothing that he touched but turned into a thing of eternal beauty. Whether it be the cross section of a skull, the structure of a weed, or a study of muscles, he, with his feeling for line and for light and shade, forever transmuted it into life-communicating values."[155]
The interest in Leonardo's genius has continued unabated; experts study and translate his writings, analyse his paintings using scientific techniques, argue over attributions and search for works which have been recorded but never found.[156] Liana Bortolon, writing in 1967, said: "Because of the multiplicity of interests that spurred him to pursue every field of knowledge...Leonardo can be considered, quite rightly, to have been the universal genius par excellence, and with all the disquieting overtones inherent in that term. Man is as uncomfortable today, faced with a genius, as he was in the 16th century. Five centuries have passed, yet we still view Leonardo with awe."[35]
Twenty-first-century author Walter Isaacson based much of his biography of Leonardo[94] on thousands of notebook entries, studying the personal notes, sketches, budget notations, and musings of the man whom he considers the greatest of innovators. Isaacson was surprised to discover a "fun, joyous" side of Leonardo in addition to his limitless curiosity and creative genius.[157]
On the 500th anniversary of Leonardo's death, the Louvre in Paris arranged for the largest ever single exhibit of his work, called Leonardo, between November 2019 and February 2020. The exhibit includes over 100 paintings, drawings and notebooks. Eleven of the paintings that Leonardo completed in his lifetime were included. Five of these are owned by the Louvre, but the Mona Lisa was not included because it is in such great demand among general visitors to the Louvre; it remains on display in its gallery. Vitruvian Man, however, is on display following a legal battle with its owner, the Gallerie dell'Accademia in Venice. Salvator Mundi [ad] was also not included because its Saudi owner did not agree to lease the work.[160][161]
The Mona Lisa, considered Leonardo's magnum opus, is often regarded as the most famous portrait ever made.[3][162] The Last Supper is the most reproduced religious painting of all time,[163] and Leonardo's Vitruvian Man drawing is also considered a cultural icon.[164]
Location of remains
While Leonardo was certainly buried in the collegiate church of Saint Florentin at the Château d'Amboise in 12 August 1519, the current location of his remains is unclear.[165][166] Much of Château d'Amboise was damaged during the French Revolution, leading to the church's demolition in 1802.[165] Some of the graves were destroyed in the process, scattering the bones interred there and thereby leaving the whereabouts of Leonardo's remains subject to dispute; a gardener may have even buried some in the corner of the courtyard.[165]
In 1863, fine-arts inspector general Arsène Houssaye received an imperial commission to excavate the site and discovered a partially complete skeleton with a bronze ring on one finger, white hair, and stone fragments bearing the inscriptions "EO", "AR", "DUS", and "VINC"—interpreted as forming "Leonardus Vinci".[87][165][167] The skull's eight teeth corresponds to someone of approximately the appropriate age and a silver shield found near the bones depicts a beardless Francis I, corresponding to the king's appearance during Leonardo's time in France.[167]
Houssaye postulated that the unusually large skull was an indicator of Leonardo's intelligence; author Charles Nicholl describes this as a "dubious phrenological deduction."[165] At the same time, Houssaye noted some issues with his observations, including that the feet were turned towards the high altar, a practice generally reserved for laymen, and that the skeleton of 1.73 metres (5.7 ft) seemed too short.[167] Art historian Mary Margaret Heaton wrote in 1874 that the height would be appropriate for Leonardo.[168] The skull was allegedly presented to Napoleon III before being returned to the Château d'Amboise, where they were re-interred in the chapel of Saint Hubert in 1874.[167][169] A plaque above the tomb states that its contents are only presumed to be those of Leonardo.[166]
It has since been theorized that the folding of the skeleton's right arm over the head may correspond to the paralysis of Leonardo's right hand.[76][82][167] In 2016, it was announced that DNA tests would be conducted to determine whether the attribution is correct.[169] The DNA of the remains will be compared to that of samples collected from Leonardo's work and his half-brother Domenico's descendants;[169] it may also be sequenced.[170]
In 2019, documents were published revealing that Houssaye had kept the ring and a lock of hair. In 1925, his great-grandson sold these to an American collector. Sixty years later, another American acquired them, leading to their being displayed at the Leonardo Museum in Vinci beginning on 2 May 2019, the 500th anniversary of the artist's death.[87][171]
Notes
General
- Salvator Mundi, a painting by Leonardo depicting Jesus holding an orb, sold for a world record US$450.3 million at a Christie's auction in New York, 15 November 2017.[158] The highest known sale price for any artwork was previously US$300 million, for Willem de Kooning's Interchange, which was sold privately in September 2015.[159] The highest price previously paid for a work of art at auction was for Pablo Picasso's Les Femmes d'Alger, which sold for US$179.4 million in May 2015 at Christie's New York.[159]
Dates of works
- Mona Lisa
- Kemp (2019, p. 127): c. 1503–1515
- Marani (2003, p. 340): c. 1503–1504; 1513–1514
- Syson et al. (2011, p. 48): c. 1502 onwards
- Zöllner (2019, p. 240): c. 1503–1506; 1510
References
Citations
Early
- Vasari 1965, p. 255
Modern
- Messia, Hada; Robinson, Matthew (30 April 2019). "Leonardo da Vinci's 'hair' to undergo DNA testing". CNN. Retrieved 3 May 2019.
Bibliography
Early
- Anonimo Gaddiano (c. 1530). "Leonardo da Vinci". Codice Magliabechiano. in Lives of Leonardo da Vinci (Lives of the Artists). Los Angeles: J. Paul Getty Museum. 2019. pp. 103–114. ISBN 978-1-60606-621-8.
- Giovio, Paolo (c. 1527). "The Life of Leonardo da Vinci". Elogia virorum illustrium. in Lives of Leonardo da Vinci (Lives of the Artists). Los Angeles: J. Paul Getty Museum. 2019. pp. 103–114. ISBN 978-1-60606-621-8.
- Vasari, Giorgio (1965) [1568]. "The Life of Leonardo da Vinci". Lives of the Artists. Translated by George Bull. Penguin Classics. ISBN 978-0-14-044164-2.
Modern
- Books
- Arasse, Daniel (1998). Leonardo da Vinci. Old Saybrook, Connecticut: Konecky & Konecky. ISBN 978-1-56852-198-5.
- Bambach, Carmen C., ed. (2003). Leonardo da Vinci, Master Draftsman. New York City, New York: Metropolitan Museum of Art. ISBN 978-0-300-09878-5.
- Bambach, Carmen C. (2019). Leonardo da Vinci Rediscovered. 1, The Making of an Artist: 1452–1500. New Haven: Yale University Press. ISBN 978-0-300-19195-0.
- Bortolon, Liana (1967). The Life and Times of Leonardo. London: Paul Hamlyn.
- Brown, David Alan (1998). Leonardo Da Vinci: Origins of a Genius. New Haven, Connecticut: Yale University Press. ISBN 978-0-300-07246-4.
- Capra, Fritjof (2007). The Science of Leonardo. US: Doubleday. ISBN 978-0-385-51390-6.
- Ottino della Chiesa, Angela (1967). The Complete Paintings of Leonardo da Vinci. Penguin Classics of World Art. London, UK: Penguin Books. ISBN 978-0-14-008649-2.
- Clark, Kenneth (1961). Leonardo da Vinci. City of Westminster, London, England: Penguin Books. OCLC 187223.
- Da Vinci, Leonardo (1971). Taylor, Pamela (ed.). The Notebooks of Leonardo da Vinci. New American Library.
- Gasca, Ana Millàn; Nicolò, Fernando; Lucertini, Mario (2004). Technological Concepts and Mathematical Models in the Evolution of Modern Engineering Systems. Birkhauser. ISBN 978-3-7643-6940-8.
- Hartt, Frederich (1970). A History of Italian Renaissance Art. Thames and Hudson. ISBN 978-0-500-23136-4.
- Heaton, Mary Margaret (1874). Leonardo Da Vinci and His Works: Consisting of a Life of Leonardo Da Vinci. New York City, New York: Macmillan Publishers. OCLC 1706262.
- Isaacson, Walter (2017). Leonardo da Vinci. New York City, New York: Simon & Schuster. ISBN 978-1-5011-3915-4.
- Kemp, Martin (2006) [1981]. Leonardo Da Vinci: The Marvellous Works of Nature and Man. Oxford, England: Oxford, England. ISBN 978-0-19-920778-7.
- Kemp, Martin (2011) [2004]. Leonardo (Revised ed.). Oxford, England: Oxford University Press. ISBN 978-0-19-280644-4.
- Kemp, Martin; Pallanti, Giuseppe (2017). Mona Lisa: The People and the Painting. Oxford, England: Oxford University Press. ISBN 978-0-19-874990-5.
- Kemp, Martin (2019). Leonardo da Vinci: The 100 Milestones. New York City, New York: Sterling. ISBN 978-1-4549-304-26.
- Magnano, Milena (2007). Leonardo, collana I Geni dell'arte. Mondadori Arte. ISBN 978-88-370-6432-7.
- Marani, Pietro C. (2003) [2000]. Leonardo da Vinci: The Complete Paintings. New York City, New York: Harry N. Abrams. ISBN 978-0-8109-3581-5.
- Martindale, Andrew (1972). The Rise of the Artist. Thames and Hudson. ISBN 978-0-500-56006-8.
- Nicholl, Charles (2005). Leonardo da Vinci: The Flights of the Mind. London, England: Penguin Books. ISBN 978-0-14-029681-5.
- O'Malley, Charles D.; Sounders, J.B. de C.M. (1952). Leonardo on the Human Body: The Anatomical, Physiological, and Embryological Drawings of Leonardo da Vinci. With Translations, Emendations and a Biographical Introduction. New York City, New York: Henry Schuman.
- Pedretti, Carlo (1982). Leonardo, a study in chronology and style. Cambridge, Massachusetts: Johnson Reprint Corp. ISBN 978-0-3844-5281-7.
- Pedretti, Carlo (2006). Leonardo da Vinci. Surrey, England: Taj Books International. ISBN 978-1-8440-6036-8.
- Popham, A.E. (1946). The Drawings of Leonardo da Vinci. Jonathan Cape. ISBN 978-0-224-60462-8.
- Richter, Jean Paul (1970). The Notebooks of Leonardo da Vinci. Dover. ISBN 978-0-486-22572-2. volume 2: ISBN 0-486-22573-9. A reprint of the original 1883 edition
- Rosci, Marco (1977). Leonardo. Bay Books Pty Ltd. ISBN 978-0-85835-176-9.
- Syson, Luke; Keith, Larry; Galansino, Arturo; Mazzotta, Antoni; Nethersole, Scott; Rumberg, Per (2011). Leonardo da Vinci: Painter at the Court of Milan. London, England: National Gallery. ISBN 978-1-85709-491-6.
- Turner, A. Richard (1993). Invention Leonardo. New York: Alfred A. Knopf. ISBN 978-0-520-08938-9.
- Wallace, Robert (1972) [1966]. The World of Leonardo: 1452–1519. New York, New York: Time-Life Books.
- Wasserman, Jack (1975). Leonardo da Vinci. New York, New York: Harry N. Abrams. ISBN 978-0-8109-0262-6.
- Williamson, Hugh Ross (1974). Lorenzo the Magnificent. Michael Joseph. ISBN 978-0-7181-1204-2.
- Vezzosi, Alessandro (1997). Leonardo da Vinci: Renaissance Man. 'New Horizons' series. Translated by Bonfante-Warren, Alexandra (English translation ed.). London: Thames & Hudson. ISBN 978-0-500-30081-7.
- Zöllner, Frank (2015). Leonardo (2nd ed.). Cologne, Germany: Taschen. ISBN 978-3-8365-0215-3.
- Zöllner, Frank (2019) [2003]. Leonardo da Vinci: The Complete Paintings and Drawings (Anniversary ed.). Cologne, Germany: Taschen. ISBN 978-3-8365-7625-3.
- Journals and encyclopedia articles
- Brown, David Alan (1983). "Leonardo and the Idealized Portrait in Milan". Arte Lombarda. 64 (4): 102–116. JSTOR 43105426. (subscription required)
- Cremante, Simona (2005). Leonardo da Vinci: Artist, Scientist, Inventor. Giunti. ISBN 978-88-09-03891-2.
- Giacomelli, Raffaele (1936). Gli scritti di Leonardo da Vinci sul volo. Roma: G. Bardi.
- Heydenreich, Ludwig Heinrich (28 April 2020). "Leonardo da Vinci | Biography, Art & Facts | Britannica". Encyclopædia Britannica. Chicago, Illinois: Encyclopædia Britannica, Inc.
- Kemp, Martin (2003). "Leonardo da Vinci". Grove Art Online. Oxford, England: Oxford University Press. doi:10.1093/gao/9781884446054.article.T050401. ISBN 978-1-884446-05-4. (subscription or UK public library membership required)
- Lupia, John N. (Summer 1994). "The Secret Revealed: How to Look at Italian Renaissance Painting". Medieval and Renaissance Times. 1 (2): 6–17. ISSN 1075-2110.
Further reading
See Kemp (2003) and Bambach (2019, pp. 442–579) for extensive bibliographies
- Vanna, Arrighi; Bellinazzi, Anna; Villata, Edoardo, eds. (2005). Leonardo da Vinci: la vera immagine: documenti e testimonianze sulla vita e sull'opera [Leonardo da Vinci: the true image: documents and testimonies on life and work] (in Italian). Florence: Giunti Editore. ISBN 978-88-09-04519-4.
- Vecce, Carlo (2006). Leonardo (in Italian). Forward by Carlo Pedretti. Rome: Salerno. ISBN 978-88-8402-548-7.
- Winternitz, Emanuel (1982). Leonardo da Vinci As a Musician. New Haven: Yale University Press. ISBN 978-0-300-02631-3.
- Leonardo da Vinci: anatomical drawings from the Royal Library, Windsor Castle. New York City, New York: The Metropolitan Museum of Art. 1983. ISBN 978-0-87099-362-6.
External links
| Library resources about Leonardo da Vinci |
| By Leonardo da Vinci |
|---|
- General
- Universal Leonardo, a database of Leonardo's life and works maintained by Martin Kemp and Marina Wallace
- Leonardo da Vinci on the National Gallery website
- Works
- Biblioteca Leonardiana, online bibliography (in Italian)
- e-Leo: Archivio digitale di storia della tecnica e della scienza, archive of drawings, notes and manuscripts
- Works by Leonardo da Vinci at Project Gutenberg
- Works by Leonardo da Vinci at LibriVox (public domain audiobooks)

- Complete text and images of Richter's translation of the Notebooks
- The Notebooks of Leonardo da Vinci
- Leonardo da Vinci
- 1452 births
- 1519 deaths
- 15th-century Italian mathematicians
- 15th-century Italian painters
- 15th-century Italian scientists
- 15th-century Italian sculptors
- 15th-century people of the Republic of Florence
- 16th-century Italian mathematicians
- 16th-century Italian painters
- 16th-century Italian scientists
- 16th-century Italian sculptors
- 16th-century LGBT people
- 16th-century people of the Republic of Florence
- Ambassadors of the Republic of Florence
- Ballistics experts
- Fabulists
- Painters from Florence
- Botanical illustrators
- Fluid dynamicists
- History of anatomy
- Italian anatomists
- Italian caricaturists
- Italian civil engineers
- 16th-century Italian inventors
- Italian male painters
- Italian male sculptors
- Italian military engineers
- Italian physiologists
- Italian Renaissance humanists
- Italian Renaissance painters
- Italian Renaissance sculptors
- Italian Roman Catholics
- Mathematical artists
- Members of the Guild of Saint Luke
- People prosecuted under anti-homosexuality laws
- Philosophical theists
- Physiognomists
- Renaissance architects
- Renaissance painters
- Renaissance scientists
- Painters from Tuscany
- Burials in France
Languages
- Kemp (2019, p. 27): c. 1481–1482
- Marani (2003, p. 338): 1481
- Syson et al. (2011, p. 56): c. 1480–1482
- Zöllner (2019, p. 222): 1481/1482
- Kemp (2019, p. 41): c. 1483–1493
- Marani (2003, p. 339): between 1483 and 1486
- Syson et al. (2011, p. 164): 1483–c. 1485
- Zöllner (2019, p. 223): 1483–1484/1485
- Kemp (2019, p. 189): c. 1507–1514
- Marani (2003, p. 340): c. 1508
- Syson et al. (2011, p. 63): c. 1500 onwards
- Zöllner (2019, p. 248): c. 1508–1516
- Kemp (2019, p. 6): c. 1473–1474
- Marani (2003, p. 338): c. 1472–1475
- Syson et al. (2011, p. 15): c. 1472–1476
- Zöllner (2019, p. 216): c. 1473–1475
- Kemp (2019, p. 31): c. 1481–1482
- Marani (2003, p. 338): probably c. 1480
- Syson et al. (2011, p. 139): c. 1488–1490
- Zöllner (2019, p. 221): c. 1480–1482
- Kemp (2019, p. 49): c. 1491
- Marani (2003, p. 339): 1489–1490
- Syson et al. (2011, p. 111): c. 1489–1490
- Zöllner (2019, p. 226): 1489/1490
- Kemp (2019, p. 67): c. 1495–1497
- Marani (2003, p. 339): between 1494 and 1498
- Syson et al. (2011, p. 252): 1492–1497/1498
- Zöllner (2019, p. 230): c. 1495–1498















![{\displaystyle {\begin{aligned}&\left(1+2\sum _{n=1}^{\infty }{\frac {\cos(n\theta )}{\cosh(n\pi )}}\right)^{-2}+\left(1+2\sum _{n=1}^{\infty }{\frac {\cosh(n\theta )}{\cosh(n\pi )}}\right)^{-2}\\[6pt]={}&{\frac {2\Gamma ^{4}\left({\frac {3}{4}}\right)}{\pi }}={\frac {8\pi ^{3}}{\Gamma ^{4}\left({\frac {1}{4}}\right)}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe1f41906de36552b7e0243e1fca8679083b79df)