Monday, November 12, 2018

Five Solids For Pi At 3.141 Ribbits

What expansion of the mind stills the frame to picture a stroke of the brush that plastered the Universe with the paints of planets as the elements shone to the photograph in a museum? As the addition touches the bare to rough draw I say note is a tone that paints explain in simplicity. Sort through a thought as the measure is air in ounces and the bucket bares the balance. Sand may be counted in grain, the beach in gallons as the moisture again changes the weight and not the measure, this is the missing piece.

Mankind is not humanity and yet the shoulder loads as the blade of grass represents the vertebrae of mathematics on the lung in fold. To envelope a sheet is to understand more than the fiber of the weave that grain is counted as thread? No, as the silk is represented again by weight as the spider is able to capture our attention in the detail by designed so specifically that the spider himself must have a brain to discuss. Conversation again brings to the dinner table the salt, oceans of salts makes the counted grain a discussion as is it a grain of salt or a count of sand?

The fact that Pi is a sign that represents nothing different than the Fibonacci numbering is odd to the fact that popular science says it is a circle as Pi at the π is the 'one in three' observation. As written
1 in 3
      1
       3.1415 and so on yet that does not seem to make a circle. With today's computer the observation
          3 3
              1
would bring on a magnificent figure of certainly beautiful symmetry possibly even explaining in simplicity dimensional shells. I wonder why physicists keep saying that
π is a circle?
Pythagoras five solids may produce for the technician an interesting beginning template:

Fibonacci number

From Wikipedia, the free encyclopedia

Jump to navigation Jump to search

A tiling with squares whose side lengths are successive Fibonacci numbers

In mathematics, the Fibonacci numbers are the numbers in the following integer sequence, called the Fibonacci sequence, and characterized by the fact that every number after the first two is the sum of the two preceding ones:^[1]^[2]

1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\;\ldots

Often, especially in modern usage, the sequence is extended by one more initial term:

0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\;\ldots

^[3]

The Fibonacci spiral: an approximation of the golden spiral created by drawing circular arcs connecting the opposite corners of squares in the Fibonacci tiling;^[4] this one uses squares of sizes 1, 1, 2, 3, 5, 8, 13 and 21.

By definition, the first two numbers in the Fibonacci sequence are either 1 and 1, or 0 and 1, depending on the chosen starting point of the sequence, and each subsequent number is the sum of the previous two.
The sequence F_n of Fibonacci numbers is defined by the recurrence relation:

F_{n}=F_{n-1}+F_{n-2},

with seed values^[1]^[2]

F_{1}=1,\;F_{2}=1

or^[5]

F_{0}=0,\;F_{1}=1.

Fibonacci numbers appear to have first arisen in perhaps 200 BC in work by Pingala on enumerating possible patterns of poetry formed from syllables of two lengths. The Fibonacci sequence is named after Italian mathematician Leonardo of Pisa, known as Fibonacci. His 1202 book Liber Abaci introduced the sequence to Western European mathematics,^[6] although the sequence had been described earlier in Indian mathematics.^[7]^[8]^[9] The sequence described in Liber Abaci began with F₁ = 1. Fibonacci numbers were later independently discussed by Johannes Kepler in 1611 in connection with approximations to the pentagon. Their recurrence relation appears to have been understood from the early 1600s, but it has only been in the past very few decades that they have in general become widely discussed.^[10]

Platonic solid

From Wikipedia, the free encyclopedia

Jump to navigation Jump to search

In three-dimensional space, a Platonic solid is a regular, convex polyhedron. It is constructed by congruent (identical in shape and size) regular (all angles equal and all sides equal) polygonal faces with the same number of faces meeting at each vertex. Five solids meet these criteria:

Tetrahedron	Cube	Octahedron	Dodecahedron	Icosahedron
Four faces	Six faces	Eight faces	Twelve faces	Twenty faces
(Animation) (3D model)	(Animation) (3D model)	(Animation) (3D model)	(Animation) (3D model)	(Animation) (3D model)

Geometers have studied the Platonic solids for thousands of years.^[1] They are named for the ancient Greek philosopher Plato who hypothesized in his dialogue, the Timaeus, that the classical elements were made of these regular solids.^[2]

History

Kepler's Platonic solid model of the Solar System from Mysterium Cosmographicum (1596)

Assignment to the elements in Kepler's Mysterium Cosmographicum

The Platonic solids have been known since antiquity. It has been suggested that certain carved stone balls created by the late Neolithic people of Scotland represent these shapes; however, these balls have rounded knobs rather than being polyhedral, the numbers of knobs frequently differed from the numbers of vertices of the Platonic solids, there is no ball whose knobs match the 20 vertices of the dodecahedron, and the arrangement of the knobs was not always symmetric.^[3]
The ancient Greeks studied the Platonic solids extensively. Some sources (such as Proclus) credit Pythagoras with their discovery. Other evidence suggests that he may have only been familiar with the tetrahedron, cube, and dodecahedron and that the discovery of the octahedron and icosahedron belong to Theaetetus, a contemporary of Plato. In any case, Theaetetus gave a mathematical description of all five and may have been responsible for the first known proof that no other convex regular polyhedra exist.
The Platonic solids are prominent in the philosophy of Plato, their namesake. Plato wrote about them in the dialogue Timaeus c.360 B.C. in which he associated each of the four classical elements (earth, air, water, and fire) with a regular solid. Earth was associated with the cube, air with the octahedron, water with the icosahedron, and fire with the tetrahedron. There was intuitive justification for these associations: the heat of fire feels sharp and stabbing (like little tetrahedra). Air is made of the octahedron; its minuscule components are so smooth that one can barely feel it. Water, the icosahedron, flows out of one's hand when picked up, as if it is made of tiny little balls. By contrast, a highly nonspherical solid, the hexahedron (cube) represents "earth". These clumsy little solids cause dirt to crumble and break when picked up in stark difference to the smooth flow of water.^{[citation needed]} Moreover, the cube's being the only regular solid that tessellates Euclidean space was believed to cause the solidity of the Earth.
Of the fifth Platonic solid, the dodecahedron, Plato obscurely remarks, "...the god used [it] for arranging the constellations on the whole heaven". Aristotle added a fifth element, aithēr (aether in Latin, "ether" in English) and postulated that the heavens were made of this element, but he had no interest in matching it with Plato's fifth solid.^[4]
Euclid completely mathematically described the Platonic solids in the Elements, the last book (Book XIII) of which is devoted to their properties. Propositions 13–17 in Book XIII describe the construction of the tetrahedron, octahedron, cube, icosahedron, and dodecahedron in that order. For each solid Euclid finds the ratio of the diameter of the circumscribed sphere to the edge length. In Proposition 18 he argues that there are no further convex regular polyhedra. Andreas Speiser has advocated the view that the construction of the 5 regular solids is the chief goal of the deductive system canonized in the Elements.^[5] Much of the information in Book XIII is probably derived from the work of Theaetetus.
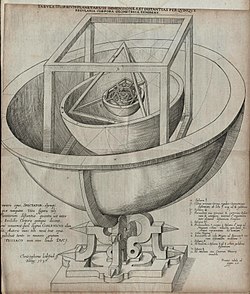
In the 16th century, the German astronomer Johannes Kepler attempted to relate the five extraterrestrial planets known at that time to the five Platonic solids. In Mysterium Cosmographicum, published in 1596, Kepler proposed a model of the Solar System in which the five solids were set inside one another and separated by a series of inscribed and circumscribed spheres. Kepler proposed that the distance relationships between the six planets known at that time could be understood in terms of the five Platonic solids enclosed within a sphere that represented the orbit of Saturn. The six spheres each corresponded to one of the planets (Mercury, Venus, Earth, Mars, Jupiter, and Saturn). The solids were ordered with the innermost being the octahedron, followed by the icosahedron, dodecahedron, tetrahedron, and finally the cube, thereby dictating the structure of the solar system and the distance relationships between the planets by the Platonic solids. In the end, Kepler's original idea had to be abandoned, but out of his research came his three laws of orbital dynamics, the first of which was that the orbits of planets are ellipses rather than circles, changing the course of physics and astronomy. He also discovered the Kepler solids.
In the 20th century, attempts to link Platonic solids to the physical world were expanded to the electron shell model in chemistry by Robert Moon in a theory known as the "Moon model".^[6]

Cartesian coordinates

For Platonic solids centered at the origin, simple Cartesian coordinates of the vertices are given below. The Greek letter φ is used to represent the golden ratio 1 + √5/2 ≈ 1.6180.

Parameters
Figure	Tetrahedron		Octahedron	Cube	Icosahedron		Dodecahedron
Faces	4		8	6	20		12
Vertices	4		6 (2 × 3)	8	12 (4 × 3)		20 (8 + 4 × 3)
Orientation set	1	2			1	2	1	2
Vertex Coordinates	(1, 1, 1) (1, −1, −1) (−1, 1, −1) (−1, −1, 1)	(−1, −1, −1) (−1, 1, 1) (1, −1, 1) (1, 1, −1)	(±1, 0, 0) (0, ±1, 0) (0, 0, ±1)	(±1, ±1, ±1)	(0, ±1, ±φ) (±1, ±φ, 0) (±φ, 0, ±1)	(0, ±φ, ±1) (±φ, ±1, 0) (±1, 0, ±φ)	(±1, ±1, ±1) (0, ±1/φ, ±φ) (±1/φ, ±φ, 0) (±φ, 0, ±1/φ)	(±1, ±1, ±1) (0, ±φ, ±1/φ) (±φ, ±1/φ, 0) (±1/φ, 0, ±φ)
Image

The coordinates for the tetrahedron, icosahedron, and dodecahedron are given in two orientation sets, each containing half of the sign and position permutation of coordinates.
These coordinates reveal certain relationships between the Platonic solids: the vertices of the tetrahedron represent half of those of the cube, as {4,3} or

, one of two sets of 4 vertices in dual positions, as h{4,3} or

. Both tetrahedral positions make the compound stellated octahedron.
The coordinates of the icosahedron are related to two alternated sets of coordinates of a nonuniform truncated octahedron, t{3,4} or

, also called a snub octahedron, as s{3,4} or

, and seen in the compound of two icosahedra.
Eight of the vertices of the dodecahedron are shared with the cube. Completing all orientations leads to the compound of five cubes.

Combinatorial properties

A convex polyhedron is a Platonic solid if and only if

all its faces are congruent convex regular polygons,
none of its faces intersect except at their edges, and
the same number of faces meet at each of its vertices.

Each Platonic solid can therefore be denoted by a symbol {p, q} where

p is the number of edges (or, equivalently, vertices) of each face, and

q is the number of faces (or, equivalently, edges) that meet at each vertex.

The symbol {p, q}, called the Schläfli symbol, gives a combinatorial description of the polyhedron. The Schläfli symbols of the five Platonic solids are given in the table below.

Polyhedron	Vertices	Edges	Faces	Schläfli symbol	Vertex configuration
tetrahedron	4	6	4	{3, 3}	3.3.3
cube	8	12	6	{4, 3}	4.4.4
octahedron	6	12	8	{3, 4}	3.3.3.3
dodecahedron	20	30	12	{5, 3}	5.5.5
icosahedron	12	30	20	{3, 5}	3.3.3.3.3

One possible Hamiltonian cycle through every vertex of a dodecahedron is shown in red – like all platonic solids, the dodecahedron is Hamiltonian

The above as a two-dimensional planar graph

All other combinatorial information about these solids, such as total number of vertices (V), edges (E), and faces (F), can be determined from p and q. Since any edge joins two vertices and has two adjacent faces we must have:

pF=2E=qV.\,

The other relationship between these values is given by Euler's formula:

V-E+F=2.\,

This can be proved in many ways. Together these three relationships completely determine V, E, and F:

V={\frac {4p}{4-(p-2)(q-2)}},\quad E={\frac {2pq}{4-(p-2)(q-2)}},\quad F={\frac {4q}{4-(p-2)(q-2)}}.

Swapping p and q interchanges F and V while leaving E unchanged. For a geometric interpretation of this property, see § Dual polyhedra below.

As a configuration

The elements of the platonic solids can be expressed in a configuration matrix. The diagonal elements represent the number of vertices, edges, and faces (f-vectors). The nondiagonal elements represent the number of row elements are incident to the column element. For example the top row shows a vertex has q edges and q faces incident, and the bottom row shows a face has p vertices, and p edges. And the middle row show an edge has 2 vertices, and 2 faces. Dual pairs of platonic solids have their configurations matrixes rotated 180 degrees from each other.^[7]

{p,q}

Platonic configurations

group order:
g = 8pq/(4-(p-2)(q-2))

g=24

g=48

g=120

	v	e	f
v	g/2q	q	q
e	2	g/4	2
f	p	p	g/2p

{3,3}
4	3	3
2	6	2
3	3	4

{3,4}
6	4	4
2	12	2
3	3	8

{4,3}
8	3	3
2	12	2
4	4	6

{3,5}
12	5	5
2	30	2
3	3	20

{5,3}
20	3	3
2	30	2
5	5	12

Classification

The classical result is that only five convex regular polyhedra exist. Two common arguments below demonstrate no more than five Platonic solids can exist, but positively demonstrating the existence of any given solid is a separate question—one that requires an explicit construction.

Geometric proof

Polygon nets around a vertex
{3,3} Defect 180°	{3,4} Defect 120°	{3,5} Defect 60°	{3,6} Defect 0°
{4,3} Defect 90°	{4,4} Defect 0°	{5,3} Defect 36°	{6,3} Defect 0°
A vertex needs at least 3 faces, and an angle defect. A 0° angle defect will fill the Euclidean plane with a regular tiling. By Descartes' theorem, the number of vertices is 720°/defect.

The following geometric argument is very similar to the one given by Euclid in the Elements:

Each vertex of the solid must be a vertex for at least three faces.
At each vertex of the solid, the total, among the adjacent faces, of the angles between their respective adjacent sides must be less than 360°. The amount less than 360° is called an angle defect.
The angles at all vertices of all faces of a Platonic solid are identical: each vertex of each face must contribute less than 360°/3 = 120°.
Regular polygons of six or more sides have only angles of 120° or more, so the common face must be the triangle, square, or pentagon. For these different shapes of faces the following holds:
- Triangular faces: Each vertex of a regular triangle is 60°, so a shape may have 3, 4, or 5 triangles meeting at a vertex; these are the tetrahedron, octahedron, and icosahedron respectively.
- Square faces: Each vertex of a square is 90°, so there is only one arrangement possible with three faces at a vertex, the cube.
- Pentagonal faces: Each vertex is 108°; again, only one arrangement of three faces at a vertex is possible, the dodecahedron.

Altogether this makes 5 possible Platonic solids.

Topological proof

A purely topological proof can be made using only combinatorial information about the solids. The key is Euler's observation that V − E + F = 2, and the fact that pF = 2E = qV, where p stands for the number of edges of each face and q for the number of edges meeting at each vertex. Combining these equations one obtains the equation

{\frac {2E}{q}}-E+{\frac {2E}{p}}=2.

Simple algebraic manipulation then gives

{1 \over q}+{1 \over p}={1 \over 2}+{1 \over E}.

Since E is strictly positive we must have

{\frac {1}{q}}+{\frac {1}{p}}>{\frac {1}{2}}.

Using the fact that p and q must both be at least 3, one can easily see that there are only five possibilities for {p, q}:

{3, 3}, {4, 3}, {3, 4}, {5, 3}, {3, 5}.

Geometric properties

Angles

There are a number of angles associated with each Platonic solid. The dihedral angle is the interior angle between any two face planes. The dihedral angle, θ, of the solid {p,q} is given by the formula

\sin {\theta  \over 2}={\frac {\cos \left({\frac {\pi }{q}}\right)}{\sin \left({\frac {\pi }{p}}\right)}}.

This is sometimes more conveniently expressed in terms of the tangent by

\tan {\theta  \over 2}={\frac {\cos \left({\frac {\pi }{q}}\right)}{\sin \left({\frac {\pi }{h}}\right)}}.

The quantity h (called the Coxeter number) is 4, 6, 6, 10, and 10 for the tetrahedron, cube, octahedron, dodecahedron, and icosahedron respectively.
The angular deficiency at the vertex of a polyhedron is the difference between the sum of the face-angles at that vertex and 2

π

. The defect, δ, at any vertex of the Platonic solids {p,q} is

\delta =2\pi -q\pi \left(1-{2 \over p}\right).

By a theorem of Descartes, this is equal to 4

π

divided by the number of vertices (i.e. the total defect at all vertices is 4

π

).
The 3-dimensional analog of a plane angle is a solid angle. The solid angle, Ω, at the vertex of a Platonic solid is given in terms of the dihedral angle by

\Omega =q\theta -(q-2)\pi .\,

This follows from the spherical excess formula for a spherical polygon and the fact that the vertex figure of the polyhedron {p,q} is a regular q-gon.
The solid angle of a face subtended from the center of a platonic solid is equal to the solid angle of a full sphere (4

π

steradians) divided by the number of faces. Note that this is equal to the angular deficiency of its dual.
The various angles associated with the Platonic solids are tabulated below. The numerical values of the solid angles are given in steradians. The constant φ = 1 + √5/2 is the golden ratio.

Polyhedron	Dihedral angle (θ)	tan θ/2	Defect (δ)	Vertex solid angle (Ω)	Face solid angle
tetrahedron	70.53°	$1 \over {\sqrt {2}}$	$\pi$	$\cos ^{-1}\left({\frac {23}{27}}\right)\quad \approx 0.551286$	$\pi$
cube	90°	$1$	$\pi \over 2$	${\frac {\pi }{2}}\quad \approx 1.57080$	$2\pi \over 3$
octahedron	109.47°	${\sqrt {2}}$	${2\pi } \over 3$	$4\sin ^{-1}\left({1 \over 3}\right)\quad \approx 1.35935$	$\pi \over 2$
dodecahedron	116.57°	$\varphi$	$\pi \over 5$	$\pi -\tan ^{-1}\left({\frac {2}{11}}\right)\quad \approx 2.96174$	$\pi \over 3$
icosahedron	138.19°	$\varphi ^{2}$	$\pi \over 3$	$2\pi -5\sin ^{-1}\left({2 \over 3}\right)\quad \approx 2.63455$	$\pi \over 5$

Radii, area, and volume

Another virtue of regularity is that the Platonic solids all possess three concentric spheres:

the circumscribed sphere that passes through all the vertices,
the midsphere that is tangent to each edge at the midpoint of the edge, and
the inscribed sphere that is tangent to each face at the center of the face.

The radii of these spheres are called the circumradius, the midradius, and the inradius. These are the distances from the center of the polyhedron to the vertices, edge midpoints, and face centers respectively. The circumradius R and the inradius r of the solid {p, q} with edge length a are given by

R=\left({a \over 2}\right)\tan {\frac {\pi }{q}}\tan {\frac {\theta }{2}}

r=\left({a \over 2}\right)\cot {\frac {\pi }{p}}\tan {\frac {\theta }{2}}

where θ is the dihedral angle. The midradius ρ is given by

\rho =\left({a \over 2}\right){\frac {\cos \left({\frac {\pi }{p}}\right)}{\sin \left({\frac {\pi }{h}}\right)}}

where h is the quantity used above in the definition of the dihedral angle (h = 4, 6, 6, 10, or 10). Note that the ratio of the circumradius to the inradius is symmetric in p and q:

{\displaystyle {R \over r}=\tan {\frac {\pi }{p}}\tan {\frac {\pi }{q}}={\frac {\sqrt {{\sin ^{-2}{\left({\frac {\theta }{2}}\right)}}-{\cos ^{2}{\left({\frac {\alpha }{2}}\right)}}}}{\sin {\left({\frac {\alpha }{2}}\right)}}}.}

The surface area, A, of a Platonic solid {p, q} is easily computed as area of a regular p-gon times the number of faces F. This is:

A=\left({a \over 2}\right)^{2}Fp\cot {\frac {\pi }{p}}.

The volume is computed as F times the volume of the pyramid whose base is a regular p-gon and whose height is the inradius r. That is,

V={\tfrac {1}{3}}rA.

The following table lists the various radii of the Platonic solids together with their surface area and volume. The overall size is fixed by taking the edge length, a, to be equal to 2.

Polyhedron (a = 2)	Inradius (r)	Midradius (ρ)	Circumradius (R)	Surface area (A)	Volume (V)	Volume (unit edges)
tetrahedron	$1 \over {\sqrt {6}}$	$1 \over {\sqrt {2}}$	${\sqrt {3 \over 2}}$	$4{\sqrt {3}}$	${\frac {\sqrt {8}}{3}}\approx 0.942809$	$\approx 0.117851$
cube	$1\,$	${\sqrt {2}}$	${\sqrt {3}}$	$24\,$	$8\,$	$1\,$
octahedron	${\sqrt {2 \over 3}}$	$1\,$	${\sqrt {2}}$	$8{\sqrt {3}}$	${\frac {\sqrt {128}}{3}}\approx 3.771236$	$\approx 0.471404$
dodecahedron	${\frac {\varphi ^{2}}{\xi }}$	$\varphi ^{2}$	${\sqrt {3}}\,\varphi$	$12{\sqrt {25+10{\sqrt {5}}}}$	${\frac {20\varphi ^{3}}{\xi ^{2}}}\approx 61.304952$	$\approx 7.663119$
icosahedron	${\frac {\varphi ^{2}}{\sqrt {3}}}$	$\varphi$	$\xi \varphi$	$20{\sqrt {3}}$	${\frac {20\varphi ^{2}}{3}}\approx 17.453560$	$\approx 2.181695$

The constants φ and ξ in the above are given by

{\displaystyle \varphi =2\cos {\pi \over 5}={\frac {1+{\sqrt {5}}}{2}}\qquad \xi =2\sin {\pi \over 5}={\sqrt {\frac {5-{\sqrt {5}}}{2}}}=5^{\frac {1}{4}}\varphi ^{-{\frac {1}{2}}}.}

Among the Platonic solids, either the dodecahedron or the icosahedron may be seen as the best approximation to the sphere. The icosahedron has the largest number of faces and the largest dihedral angle, it hugs its inscribed sphere the most tightly, and its surface area to volume ratio is closest to that of a sphere of the same size (i.e. either the same surface area or the same volume.) The dodecahedron, on the other hand, has the smallest angular defect, the largest vertex solid angle, and it fills out its circumscribed sphere the most.

Symmetry

Dual polyhedra

Dual compounds

Every polyhedron has a dual (or "polar") polyhedron with faces and vertices interchanged. The dual of every Platonic solid is another Platonic solid, so that we can arrange the five solids into dual pairs.

The tetrahedron is self-dual (i.e. its dual is another tetrahedron).
The cube and the octahedron form a dual pair.
The dodecahedron and the icosahedron form a dual pair.

If a polyhedron has Schläfli symbol {p, q}, then its dual has the symbol {q, p}. Indeed, every combinatorial property of one Platonic solid can be interpreted as another combinatorial property of the dual.
One can construct the dual polyhedron by taking the vertices of the dual to be the centers of the faces of the original figure. Connecting the centers of adjacent faces in the original forms the edges of the dual and thereby interchanges the number of faces and vertices while maintaining the number of edges.
More generally, one can dualize a Platonic solid with respect to a sphere of radius d concentric with the solid. The radii (R, ρ, r) of a solid and those of its dual (R*, ρ*, r*) are related by

d^{2}=R^{\ast }r=r^{\ast }R=\rho ^{\ast }\rho .

Dualizing with respect to the midsphere (d = ρ) is often convenient because the midsphere has the same relationship to both polyhedra. Taking d² = Rr yields a dual solid with the same circumradius and inradius (i.e. R* = R and r* = r).

Symmetry groups

In mathematics, the concept of symmetry is studied with the notion of a mathematical group. Every polyhedron has an associated symmetry group, which is the set of all transformations (Euclidean isometries) which leave the polyhedron invariant. The order of the symmetry group is the number of symmetries of the polyhedron. One often distinguishes between the full symmetry group, which includes reflections, and the proper symmetry group, which includes only rotations.
The symmetry groups of the Platonic solids are a special class of three-dimensional point groups known as polyhedral groups. The high degree of symmetry of the Platonic solids can be interpreted in a number of ways. Most importantly, the vertices of each solid are all equivalent under the action of the symmetry group, as are the edges and faces. One says the action of the symmetry group is transitive on the vertices, edges, and faces. In fact, this is another way of defining regularity of a polyhedron: a polyhedron is regular if and only if it is vertex-uniform, edge-uniform, and face-uniform.
There are only three symmetry groups associated with the Platonic solids rather than five, since the symmetry group of any polyhedron coincides with that of its dual. This is easily seen by examining the construction of the dual polyhedron. Any symmetry of the original must be a symmetry of the dual and vice versa. The three polyhedral groups are:

the tetrahedral group T,
the octahedral group O (which is also the symmetry group of the cube), and
the icosahedral group I (which is also the symmetry group of the dodecahedron).

The orders of the proper (rotation) groups are 12, 24, and 60 respectively – precisely twice the number of edges in the respective polyhedra. The orders of the full symmetry groups are twice as much again (24, 48, and 120). See (Coxeter 1973) for a derivation of these facts. All Platonic solids except the tetrahedron are centrally symmetric, meaning they are preserved under reflection through the origin.
The following table lists the various symmetry properties of the Platonic solids. The symmetry groups listed are the full groups with the rotation subgroups given in parenthesis (likewise for the number of symmetries). Wythoff's kaleidoscope construction is a method for constructing polyhedra directly from their symmetry groups. They are listed for reference Wythoff's symbol for each of the Platonic solids.

Polyhedron	Schläfli symbol	Wythoff symbol	Dual polyhedron	Symmetry group (Reflection, rotation)
Polyhedron	Schläfli symbol	Wythoff symbol	Dual polyhedron	Polyhedral	Schön.	Cox.	Orb.	Order
tetrahedron	{3, 3}	3 \| 2 3	tetrahedron	Tetrahedral	T_d T	[3,3] [3,3]⁺	*332 332	24 12
cube	{4, 3}	3 \| 2 4	octahedron	Octahedral	O_h O	[4,3] [4,3]⁺	*432 432	48 24
octahedron	{3, 4}	4 \| 2 3	cube	Octahedral	O_h O	[4,3] [4,3]⁺	*432 432	48 24
dodecahedron	{5, 3}	3 \| 2 5	icosahedron	Icosahedral	I_h I	[5,3] [5,3]⁺	*532 532	120 60
icosahedron	{3, 5}	5 \| 2 3	dodecahedron	Icosahedral	I_h I	[5,3] [5,3]⁺	*532 532	120 60

In nature and technology

This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (October 2018) (Learn how and when to remove this template message)

The tetrahedron, cube, and octahedron all occur naturally in crystal structures. These by no means exhaust the numbers of possible forms of crystals. However, neither the regular icosahedron nor the regular dodecahedron are amongst them. One of the forms, called the pyritohedron (named for the group of minerals of which it is typical) has twelve pentagonal faces, arranged in the same pattern as the faces of the regular dodecahedron. The faces of the pyritohedron are, however, not regular, so the pyritohedron is also not regular. Allotropes of boron and many boron compounds, such as boron carbide, include discrete B₁₂ icosahedra within their crystal structures. Carborane acids also have molecular structures approximating regular icosahedra.

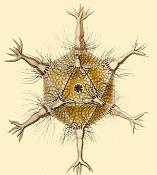
Circogonia icosahedra, a species of radiolaria, shaped like a regular icosahedron.

In the early 20th century, Ernst Haeckel described (Haeckel, 1904) a number of species of Radiolaria, some of whose skeletons are shaped like various regular polyhedra. Examples include Circoporus octahedrus, Circogonia icosahedra, Lithocubus geometricus and Circorrhegma dodecahedra. The shapes of these creatures should be obvious from their names.
Many viruses, such as the herpes virus, have the shape of a regular icosahedron. Viral structures are built of repeated identical protein subunits and the icosahedron is the easiest shape to assemble using these subunits. A regular polyhedron is used because it can be built from a single basic unit protein used over and over again; this saves space in the viral genome.
In meteorology and climatology, global numerical models of atmospheric flow are of increasing interest which employ geodesic grids that are based on an icosahedron (refined by triangulation) instead of the more commonly used longitude/latitude grid. This has the advantage of evenly distributed spatial resolution without singularities (i.e. the poles) at the expense of somewhat greater numerical difficulty.
Geometry of space frames is often based on platonic solids. In the MERO system, Platonic solids are used for naming convention of various space frame configurations. For example, 1/2O+T refers to a configuration made of one half of octahedron and a tetrahedron.
Several Platonic hydrocarbons have been synthesised, including cubane and dodecahedrane.

Platonic solids are often used to make dice, because dice of these shapes can be made fair. 6-sided dice are very common, but the other numbers are commonly used in role-playing games. Such dice are commonly referred to as dn where n is the number of faces (d8, d20, etc.); see dice notation for more details.

A set of polyhedral dice.

These shapes frequently show up in other games or puzzles. Puzzles similar to a Rubik's Cube come in all five shapes – see magic polyhedra.

Liquid crystals with symmetries of Platonic solids

For the intermediate material phase called liquid crystals, the existence of such symmetries was first proposed in 1981 by H. Kleinert and K. Maki.^[8]^[9] In aluminum the icosahedral structure was discovered three years after this by Dan Shechtman, which earned him the Nobel Prize in Chemistry in 2011.

Related polyhedra and polytopes

Uniform polyhedra

There exist four regular polyhedra which are not convex, called Kepler–Poinsot polyhedra. These all have icosahedral symmetry and may be obtained as stellations of the dodecahedron and the icosahedron.

cuboctahedron	icosidodecahedron

The next most regular convex polyhedra after the Platonic solids are the cuboctahedron, which is a rectification of the cube and the octahedron, and the icosidodecahedron, which is a rectification of the dodecahedron and the icosahedron (the rectification of the self-dual tetrahedron is a regular octahedron). These are both quasi-regular, meaning that they are vertex- and edge-uniform and have regular faces, but the faces are not all congruent (coming in two different classes). They form two of the thirteen Archimedean solids, which are the convex uniform polyhedra with polyhedral symmetry. Their duals, the rhombic dodecahedron and rhombic triacontahedron, are edge- and face-transitive, but their faces are not regular and their vertices come in two types each; they are two of the thirteen Catalan solids.
The uniform polyhedra form a much broader class of polyhedra. These figures are vertex-uniform and have one or more types of regular or star polygons for faces. These include all the polyhedra mentioned above together with an infinite set of prisms, an infinite set of antiprisms, and 53 other non-convex forms.
The Johnson solids are convex polyhedra which have regular faces but are not uniform. Among them are five of the eight convex deltahedra, which have identical, regular faces (all equilateral triangles) but are not uniform. (The other three convex deltahedra are the Platonic tetrahedron, octahedron, and icosahedron.)

Regular tessellations

Regular spherical tilings
Platonic tilings

{3,3}	{4,3}	{3,4}	{5,3}	{3,5}
Regular dihedral tilings

{2,2}	{3,2}	{4,2}	{5,2}	{6,2}...
Regular hosohedral tilings

{2,2}	{2,3}	{2,4}	{2,5}	{2,6}...

The three regular tessellations of the plane are closely related to the Platonic solids. Indeed, one can view the Platonic solids as regular tessellations of the sphere. This is done by projecting each solid onto a concentric sphere. The faces project onto regular spherical polygons which exactly cover the sphere. Spherical tilings provide two infinite additional sets of regular tilings, the hosohedra, {2,n} with 2 vertices at the poles, and lune faces, and the dual dihedra, {n,2} with 2 hemispherical faces and regularly spaced vertices on the equator. Such tesselations would be degenerate in true 3D space as polyhedra.
One can show that every regular tessellation of the sphere is characterized by a pair of integers {p, q} with 1/p + 1/q > 1/2. Likewise, a regular tessellation of the plane is characterized by the condition 1/p + 1/q = 1/2. There are three possibilities:

The three regular tilings of the Euclidean plane
{4, 4}	{3, 6}	{6, 3}

In a similar manner, one can consider regular tessellations of the hyperbolic plane. These are characterized by the condition 1/p + 1/q < 1/2. There is an infinite family of such tessellations.

Example regular tilings of the hyperbolic plane
{5, 4}	{4, 5}	{7, 3}	{3, 7}

Higher dimensions

In more than three dimensions, polyhedra generalize to polytopes, with higher-dimensional convex regular polytopes being the equivalents of the three-dimensional Platonic solids.
In the mid-19th century the Swiss mathematician Ludwig Schläfli discovered the four-dimensional analogues of the Platonic solids, called convex regular 4-polytopes. There are exactly six of these figures; five are analogous to the Platonic solids 5-cell as {3,3,3}, 16-cell as {3,3,4}, 600-cell as {3,3,5}, tesseract as {4,3,3}, and 120-cell as {5,3,3}, and a sixth one, the self-dual 24-cell, {3,4,3}.
In all dimensions higher than four, there are only three convex regular polytopes: the simplex as {3,3,...,3}, the hypercube as {4,3,...,3}, and the cross-polytope as {3,3,...,4}.^[10] In three dimensions, these coincide with the tetrahedron as {3,3}, the cube as {4,3}, and the octahedron as {3,4}.

References

Gardner (1987): Martin Gardner wrote a popular account of the five solids in his December 1958 Mathematical Games column in Scientific American.

Coxeter 1973, p. 136.

Sources

Atiyah, Michael; Sutcliffe, Paul (2003). "Polyhedra in Physics, Chemistry and Geometry". Milan J. Math. 71: 33–58. arXiv:math-ph/0303071. doi:10.1007/s00032-003-0014-1.

Boyer, Carl; Merzbach, Uta (1989). A History of Mathematics (2nd ed.). Wiley. ISBN 0-471-54397-7.

Coxeter, H. S. M. (1973). Regular Polytopes (3rd ed.). New York: Dover Publications. ISBN 0-486-61480-8.

Euclid (1956). Heath, Thomas L., ed. The Thirteen Books of Euclid's Elements, Books 10–13 (2nd unabr. ed.). New York: Dover Publications. ISBN 0-486-60090-4.

Gardner, Martin(1987). The 2nd Scientific American Book of Mathematical Puzzles & Diversions, University of Chicago Press, Chapter 1: The Five Platonic Solids, ISBN 0226282538
Haeckel, Ernst, E. (1904). Kunstformen der Natur. Available as Haeckel, E. (1998); Art forms in nature, Prestel USA. ISBN 3-7913-1990-6.
Hecht, Laurence; Stevens, Charles B. (Fall 2004). "New Explorations with The Moon Model" (PDF). 21st Century Science and Technology. p. 58.
Kepler. Johannes Strena seu de nive sexangula (On the Six-Cornered Snowflake), 1611 paper by Kepler which discussed the reason for the six-angled shape of the snow crystals and the forms and symmetries in nature. Talks about platonic solids.
Kleinert, Hagen and Maki, K. (1981). "Lattice Textures in Cholesteric Liquid Crystals" (PDF). Fortschritte der Physik. 29 (5): 219–259. Bibcode:1981ForPh..29..219K. doi:10.1002/prop.19810290503

Lloyd, David Robert (2012). "How old are the Platonic Solids?". BSHM Bulletin: Journal of the British Society for the History of Mathematics. 27 (3): 131–140. doi:10.1080/17498430.2012.670845.

Pugh, Anthony (1976). Polyhedra: A visual approach. California: University of California Press Berkeley. ISBN 0-520-03056-7.
Weyl, Hermann (1952). Symmetry. Princeton, NJ: Princeton University Press. ISBN 0-691-02374-3.

Wildberg, Christian (1988). John Philoponus' Criticism of Aristotle's Theory of Aether. Walter de Gruyter. pp. 11–12. ISBN 9783110104462

External links

Wikimedia Commons has media related to Platonic solids.

Platonic solids at Encyclopaedia of Mathematics
Weisstein, Eric W. "Platonic solid". MathWorld.
Weisstein, Eric W. "Isohedron". MathWorld.
Book XIII of Euclid's Elements.
Interactive 3D Polyhedra in Java
Solid Body Viewer is an interactive 3D polyhedron viewer which allows you to save the model in svg, stl or obj format.
Interactive Folding/Unfolding Platonic Solids in Java
Paper models of the Platonic solids created using nets generated by Stella software
Platonic Solids Free paper models(nets)
Grime, James; Steckles, Katie. "Platonic Solids". Numberphile. Brady Haran.
Teaching Math with Art student-created models
Teaching Math with Art teacher instructions for making models
Frames of Platonic Solids images of algebraic surfaces
Platonic Solids with some formula derivations
How to make four platonic solids from a cube

Convex polyhedra

Platonic solids (regular)

Archimedean solids
(semiregular or uniform)

Catalan solids
(duals of Archimedean)

Dihedral regular

dihedron
hosohedron

Dihedral uniform

prisms antiprisms
duals:	bipyramids trapezohedra

Dihedral others

Degenerate polyhedra are in italics.

Categories:

Platonic solids

Languages

Zeyl, Donald. "Plato's Timaeus". The Stanford Encyclopedia of Philosophy.

Lloyd 2012.

Wildberg (1988): Wildberg discusses the correspondence of the Platonic solids with elements in Timaeus but notes that this correspondence appears to have been forgotten in Epinomis, which he calls "a long step towards Aristotle's theory", and he points out that Aristotle's ether is above the other four elements rather than on an equal footing with them, making the correspondence less apposite.

Weyl 1952, p. 74.

Hecht & Stevens 2004.

Coxeter, Regular Polytopes, sec 1.8 Configurations

Kleinert and Maki (1981)

The liquid-crystalline blue phases (1989). by Tamar Seideman, Reports on Progress in Physics, Volume 53, Number 6

Karen Placek

Presents, a Life with a Plan. My name is Karen Anastasia Placek, I am the author of this Google Blog. This is the story of my journey, a quest to understanding more than myself. The title of my first blog delivered more than a million views!! The title is its work as "The Secret of the Universe is Choice!; know decision" will be the next global slogan. Placed on T-shirts, Jackets, Sweatshirts, it really doesn't matter, 'cause a picture with my slogan is worth more than a thousand words, it's worth??.......Know Conversation!!!

Hi, where are you from?